红黑叔

news/2024/11/22 4:57:24/

 转载地址：http://blog.csdn.net/kfanning/article/details/6977393

树型结构一直是一种很重要的数据结构, 我们知道二叉查找树BST提供了一种快速查找, 插入的数据结构. 相比散列表来说BST占用空间更小,对于数据量较大和空间要求较高的场合, BST就显得大有用处了.BST的大部分操作平均运行时间为O(logN), 但是如果树是含N个结点的线性链,则最坏情况运行时间会变为O(N). 为了避免出现最坏情况我们给它增加一些平衡条件, 使它的高度最多为2log(N+1), 最坏情况下运行是间花费也接近O(logN), 这就是我下面要讨论的红黑树.由于红黑树的插入和删除是相对复杂的操作,所以这里我将重点讨论这两种操作.

AVL树

在理解红黑树之前最好先来看看AVL树, 相比红黑树AVL树在插入操作时需要更多的调整次数, 但更容易理解. 所谓AVL树就是每个节点的左子树和右子树的高度最多差1的二叉查找树.为什么是差1而不是具有相同高度?因为如果要求左右子树高度相同, 那么就只有具有2k-1个节点的树才满足条件, 这样的条件我们没法做到. 于是需要放宽条件, 允许左右子树高度差1.  下图显示一棵AVL树:

 1-1
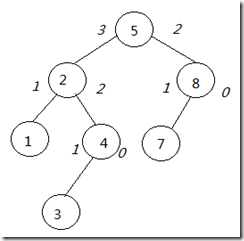
              AVL树, 结点两边为子树的高度

下面以AVL树的插入操作为例说明AVL树是如何自动平衡的, 这将有助于我们后面理解红黑树的插入. 考虑当我们向AVL树中插入一新节点后可能破坏AVL树的特性, 即某结点的左右子树高差大于1. 如果发生这种情况,就要对树进行旋转来修正, 什么是旋转? 在下面我将会解释这种步骤. 如果插入没有破坏AVL树的特性, 则可以按正常插入. 让我们假设现在有一个必须重新平衡的节点a,  由于任意节点最多有两个儿子,因此高度不平衡时,a点的两棵子树的高度差为2. 容易想到, 这种不平衡可能出现下面四种情况:
1) 对a的左儿子的左子树进行一次插入 
2) 对a的左儿子的右子树进行一次插入 
3) 对a的右儿子的左子树进行一次插入 
4) 对a的右儿子的右子树进行一次插入

情况1和4是插入发生在"外边"的情况(即左-左的情况和右-右的情况),该情况通过对树的一次单旋转而完成调整.第2和3种情况是插入发生在"内部"的情况(即左-右的情况或右-左的情况), 该情况要通过稍复杂的双旋转来处理.下面先让我们来看单旋转时的情况.

假设AVL树开始有两个结点3和2, 如下图. 当我们插入新结点1时, AVL特性被破坏, 在结点3上左子树的高度2, 而右子树高度为0. 很明显结点1位于结点3的左儿子的左子树中, 于是我们需要在根与左儿子之间施行单旋转来修正. 如下图所示: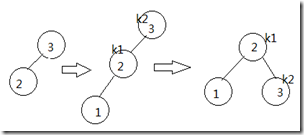
1-2

图中间为插入后的状态, 右边为旋转后的状态. 这里我们设k2为指向结点3的指针, k1为指向结点2的指针,不存在的结点用NULL表示,  则完成上面的旋转实际的代码为:
k2->left = k1->right; 
k1->right = k2;

我们看到旋转完成后树的高度降低了,而树的性质没有被破坏, 由此可以看出旋转实际是对树的变型. 由于旋转后, 靠左边的结点2被提升到上一层,而靠右边的结点3被降到下一层,因此这种的单旋操作被称为右旋. 下面我们继续插入关键字4和5. 在插入5时又破坏了节点3处的AVL特性, 于是我们通过再一次单旋转将其修正, 如下图:

1-3

这里我们设K1指向结点3, k2指向结点4, 则完成上面旋转的代码如下: 
k1->right = k2->left; 
k2->left = K1;

注意上面代码中还没有将结点2的右儿子设置为指向结点4, 在后面的完整的插入代码中我将会补上. 可以看到这次的旋转与上一次旋转的方向相反,所以称为左旋. 另外要注意的是我们在修正时采用的是至下而上的检测, 即总是从新插入结点开始, 沿插入路径向上走到根来判断是否出现高度不平衡的情况, 当发现第一个不平衡的结点时就进行修正.下面我们来看插入结点6情况.

1-4

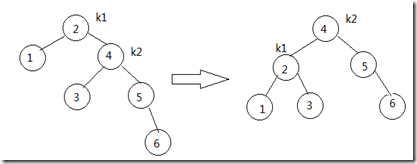
这次我们从插入路径向上直到根结点才发现不平衡, 因此旋转发生在结点2和结点4之间. 旋转与上一次相同也是一个左旋, 因为对应前面的是第4种情况, 即结点6的插入是对k1的右儿子的右子树的插入, 代码与上面相同. 下面我们继续依次插入结点7, 16和15.  首先插入的7和16没有破坏AVL树的性质, 在插入15时却会引起节点7处的高度不平衡, 如下图. 这属于前面讲到的第3种情况, 需要一次右-左双旋来修正.  

1-5

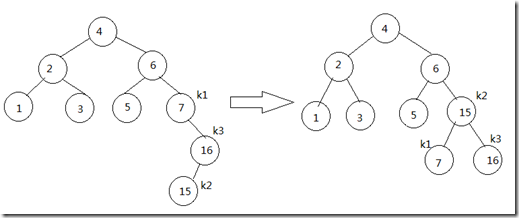
这次我们让k1指向结点7, k3指向结点16, k2指向结点15. 先在k2和k3之间作一次右旋,然后在k1和k2之间作一次左旋来完成修正, 相应代码如下:
k3->left = k2->right; 
k2->right = k3; 
k1->right = k2->left; 
k2->left = k1;

你会发现这段代码完全是上面右旋代码与左旋代码的合并, 所以所谓右-左双旋就是对树先右旋一次再左旋一次. 下面我们插入14, 它也需要一个双旋, 如下图所示. 当我们沿插入路径向上时在结点6碰到高度不平衡, 此时我们观察到结点14是位于结点6的右儿子的左子树中,因此与上一次相同属于第3种情况.修正办法还是右-左双旋转.

1-6

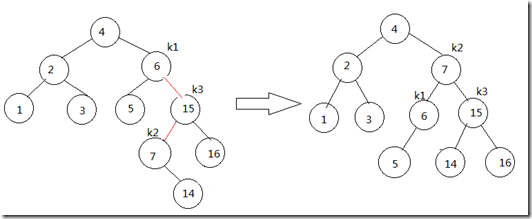
跟据上面例子分析相信你已经明白AVL树是如何利用旋转来达到平衡的了, 而旋转的主要思想就是在不破坏树的性质下对树进行变型, 使树的高度降低. 下面是AVL树插入操作的递归代码实现:

typedef struct Node *Position; 
typedef struct Node *Tree; 

struct Node 
{ 
    ElementType  element; 
    Tree  left; 
    Tree  right; 
    int     height; 
}; 

int Height(Position p) 
{ 
    if (p == NULL) return –1; 
    else return p->height; 
} 

Position SingleRightRotate(Position k2) 
{ 
    Position k1; 
    k1 = k2->left; 
    k2->left = k1->right; 
    k1->right = k2; 
    k2->height = Max(Height(k2->left), Height(k2->right)) + 1; 
    k1->height = Max(Height(k1->left), k2->height) + 1; 
    return k1; 
} 

Position DoubleRightRotate(Position k3) 
{ 
    k3->left = SingleLeftRotate(k3->left); 
    return SingleRightRotate(k3); 
} 

Tree Insert(ElementType x, Tree t) 
{ 
    if (t == NULL) { 
        t = malloc(sizeof(struct Node)); 
        t->element = x; t->height = 0; 
        t->left = t->right = NULL; 
    } else if (x < t->element) { 
        t->left = Insert(x, t->left); 
        if (Height(t->left) – Height(t->right) == 2) 
            if (x < t->left->element) 
                t = SingleRightRotate( t ); 
            else 
                t = DoubleRightRotate( t ); 
    } else if (x < t->element) { 
        t->right = Insert(x, t->right); 
        if (Height(t->right) – Height(t->left) == 2) 
            if (x > t->right->element) 
                t = SingleLeftRotate( t ); 
            else 
                t = DoubleLeftRotatel( t ); 
    } 
    t->height = Max(Height(t->left), Height(t->right)) + 1; 
    return t; 
}

在上面的代码中, SingleRightRotate函数实现右旋, 左旋SingleLeftRotate函数与右旋代码对称; Insert函数首先递归找到插入的位置并产生新结点, 然后判断结点高度是否破坏平衡条件, 如果平衡条件被破坏则通过旋转修正, 最后更新根结点.

红黑树

红黑树是AVL树的变种, 红黑树通过一些着色法则确保没有一条路径会比其它路径长出两倍,因而达到接近平衡目的.本文下面将重点讨论红黑树的插入和删除操作. 红黑树的性质如下:
1) 每一个节点或者着红色,或者着成黑色. 
2) 根是黑色的 
3) 如果一个节点是红色的,那么它的子节点必须是黑色的. 
4) 从一个节点到一个NULL指针的每一条路径必须包含相同数目的黑色节点.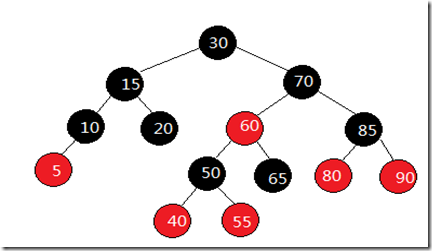  
1-7

还是以插入操作开始,红黑树的性质1和性质2对插入操作没有影响,当一个新结点被插入时, 如果该结点是黑色则肯定违反条件4, 因此新结点必须是红色. 如果新结点的父结点是黑的,则我们插入完成, 没有性质被违反. 如果父节点已经是红的,那么我们得到连续红色节点,这就违反了条件3.   在这种情况下, 我们必须调整该树以确保条件3满足且不会破坏条件4.注意在这里我们依然使用从下到上的调整过程, 即我们从新结点沿插入路径向上对结点颜色调整和旋传来保待树的性质.另一种办法是使用从上到下的调整过程. 

如上所述在从下到时上的调整过程中, 当我们遇到连续红色节点时需要对树进行调整, 这里我们设新结点为z, z的叔叔结点为y, 一共有三种情况需要处理, 实际上有一共有六种情况,但其中三种与另外三种相互对称, 这可以通过z的父结点是在其祖父结点的左子树中还是右子树中来判断. 下面我们只讨论z的父结点是在左子树的情况:

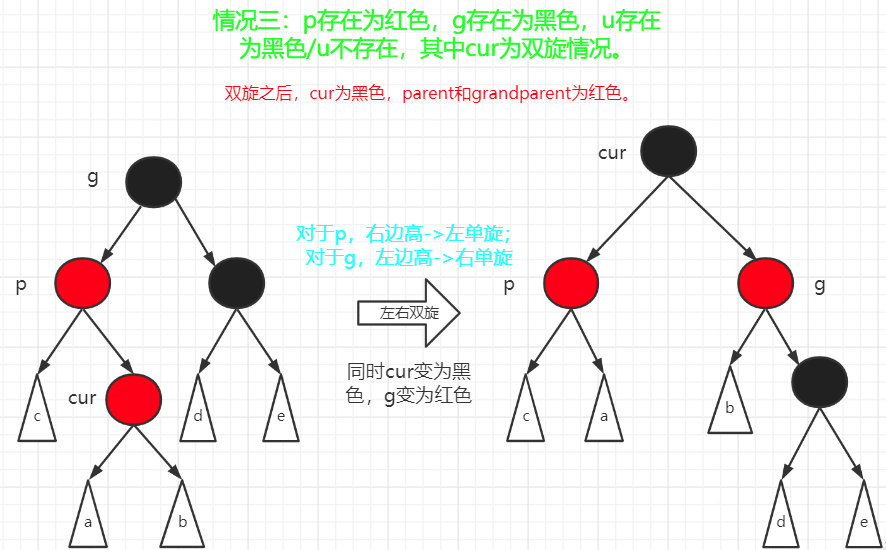
1) z的叔叔y是红色的, 如下图, 这种情况下调整办法非常简单, 不论z位于红结点的左子树还是右子树, 只需将z的父结点和叔叔结点都翻转为黑色, z的祖父结点翻转成红色即可. 但到这里并没有结束整个调整过程, 因为z的祖父结点仍可能遇到连续红节点的情况, 所以最后我们将祖父结点当作新增结点z来继续向上调整.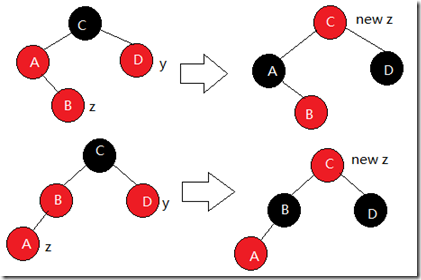
1-8

相应代码如下: 
z->parent->color = BLACK; 
y->color = BLACK; 
z->parent->parent = RED; 
z = z->parent->parent;

2) z的叔叔y是黑色的,而且z是右孩子 
3) z的叔叔y是黑色的,而且z是左孩子 
如下图, 在情况2和情况3中, z的叔叔是黑色的.这两种情况是通过判断z是其父结点的左孩子还是右孩子来区别的. 如果是情况2,则我们使用一个左旋来将状况转变为情况3. 此时结点z可以看作是左孩子. 在情况3中我们先把z的祖父结点颜色翻转为红色, 把z的父结点翻转为黑色, 并作一次右旋传. 此时两个连续的红结点已经消除, 红黑树性质没有改变, 整个调整过程处理完毕.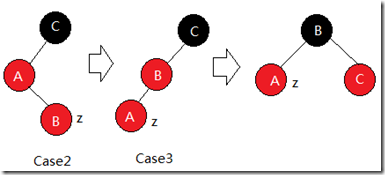  
1-9
下面是相应代码: 
if (z == z->parent->right) { 
    z = z->parent; 
    LeftRotate( z ); 
} 
z->parent->color = BLACK; 
z->parent->parent->color = RED; 
RightRotate( z->parent->parent );

从上面的分析可以看出整个调整过程由性质3触发, 同时在调整过程中确保了性质4不被破坏. 红黑树在插入过程中碰到旋转的情况比AVL树要少得多, 其原理来源于2-3-4树, 当两个连续的红结点出现时,相当于发现一个2-3-4树中的4结点,因此需要向上分裂.有兴趣的同学可以参考2-3-4树的原理. 接下来就让我们实现整个插入操作, 我们将使用非递归的方法来实现. 尽管有些书上是用递归来实现, 但红黑树的魅力却在于非递归的实现上.首先我们要对上面AVL的树结构定义作一些修改, 使之成为红黑树结构. 代码如下:

typedef enum Color { RED, BLACK } Color; 

struct Node 
{ 
    ElementType element; 
    Tree left; 
    Tree right;  
    Tree parent; 
    Color color;  
}; 

Position NullNode = NULL; 
Position RootNode = NULL; 

Node结构的parent成员指向父结点, color指出该结点的颜色. 在上面我们还增加一个全局的空结点NullNode, 空结点将在初始化时被创建, 该空结点的左右子树指向自身,且颜色为黑. 当创建一个新结点时, 我们总是将新结点的左右子树指向它. 另外我们维护一个指向根结点的指针RootNode, 并且我们还设定根结点的父结点也指向NullNode. 好了, 下面就来看看如何实现插入代码:

void RBTInsert(ElementType e) 
{ 
    Position z, y, x; 
    y = NullNode; 
    x = RootNode; 
    z = CreateNode(e); 
    while (x != NullNode) { 
        y = x; 
        if (z->element < x->element) 
            x = x->left; 
        else 
            x = x->right; 
    } 
    z->parent = y; 
    if (y == NullNode) { 
        RootNode = z; 
    } else { 
        if (z-> element < y->element)  
            y->left = z; 
        else 
            y->right = z; 
    } 
    z->left = z->right = NullNode; 
    z->color = RED; 
    RBTInsertFixup( z ); 
}

RBTInsert其实跟普通BST的插入差不多, 首先沿树根向下比较元素值并将新结点z插入正确位置(注意我们将新结点的颜色设为红的). 最后调用RBTInsertFixup来对结点进行修正. CreateNode用来创建一个新结点, 这里没有给出代码,相信你可以轻松实现它.

void RBTInsertFixup(Position z) 
{ 
    while (z->parent->color == RED) { 
        if (z->parent == z->parent->parent->left) { 
            y = z->parent->parent->right; 
            if (y->color == RED) { 
                z->parent->color = BLACK; 
                y->color = BLACK; 
                z->parent->parent->color = RED; 
                z = z->parent->parent; 
            } else { 
                if (z ==  z->parent->right) { 
                    z = z->parent; 
                    LeftRotate( z ); 
                } 
                z->parent->color = BLACK; 
                z->parent->parent->color = RED; 
                RightRotate(z->parent->parent); 
            } 
        } else { 
             /* 这里的代码与上面代码相对称, 只要将所有right和left交换就可以了 */ 
        } 
    } 
    RootNode->color = BLACK; 
} 

RBTInsertFixup实现了整个树的修正过程, 首先while循环判断是否出现连续的红结点, 接着下面的if判断新结点z的父结点, 是在其祖父结点的左子树还是右子树中. 由于右子树的修正代码与左子树的代码完全对称, 所以就不再重复了. 这里你可能会担心z指向的结点如果是根结点时, 对其祖父结点的访问会有问题. 其实不用担心, 因为前面我们说过根结点的父结点指向的是空结点, 而空结点的左右孩子指向自已, 并且空结点的颜色为黑色.所以根结点永远不会进入while循环, 在while循环结束后,我们又将根结点的颜色设回黑色, 保证了红黑树性质2不被破坏. 同时我们也不用担心对树边界的访问, 这也是为什么要在实现中增加空结点的原因.接下来的代码判断z的叔叔的结点y是否为红色,对应前面讲到的第1种情况. 如果y不是红色则要进行旋转,分别对应第2,3种情况.下面是左旋的代码, 同样右旋的代码与它对称, 我不再重复.   

void LeftRotate(Position x) 
{ 
    Position y = x->right; 
    x->right = y->left; 
    if (y->left != NullNode) 
        y->left->parent = x; 
    y->parent = x->parent; 
    if (x->parent == NullNode) { 
        RootNode = y; 
    } else { 
        if (x == x->parent->left)  
            x->parent->left = y;  
        else 
            x->parent->right = y; 
    } 
    y->left = x; 
    x->parent = y; 
} 

上面的左旋代码比前面AVL的左旋代码稍复杂一些, 主要是增加了父指针更新操作, 即在修改两个相邻结点路径时,要同时修改子结点和指针和父结点指针. 另外由于我们使用非递归的实现, 所以要显式的更新x的父结点指针.

删除

红黑树的删除比插入情况复杂, 尽管一般我们会使用"墮性删除", 即在删除操作中不对结点进行删除,而是对结点进行标记, 当有新数据插入时再将它放到原来的结点上. 不管怎样我们还是要讨论真正删除情况. 首先考虑我们要删除结点的颜色, 如果是红色, 则删除一个红色结点不会破坏红黑树的性质, 所以删除方法与在BST的删除没有差别. 如果结点是黑色, 则会遇到下面的情况:
1) 如果要删除的是根结点,  且根结点的一个红色孩子结点将成为新的根, 这就违反了性质2; 
2) 如果删除某个结点后, 在其原来父结点上出现连续的红结点, 则违反了性质4; 
3) 删除某个结点后, 导致先前包含该结点的路径上黑结点数少1, 因此违反了性质5;

下面我们就来讨论如何恢复性质2,4,5, 注意我们仍然采用从下到上的调整方法. 从上面的情况看, 恢复性质2和性质4是很简单的, 只要翻转被删除结点的子结点颜色为黑色就可以了, 关键是要保证性质5不被破坏, 即从树根到每个叶节点的黑结点个数相同, 为了做到这一点我们必须对一些结点进行旋转和改变颜色. 让我先设y指向要删除的结点,  x指向y的子结点, w指向x的兄弟结点. 当y被删除后, 如果y的颜色为红色则不需要调整, 相反如果y为黑色, 则要检查x此时是否是根, 如果是根那么直接将其颜色设为黑色,结束调整.如果x不是根, 但颜色是红, 情况相同, x直接翻转为黑色完事. 因为被删除的结点为黑, 相当于在删除y后, 所有经过x的路径上的黑结点数都少1, 所以需要补回来, 保证性质5没有被破坏. 注意此时x可能是指向空结点, 这没有什么问题, 因为空结点是黑的, 所以会进入下面的调整过程.

接着往下分析, 如果x此时是黑的就复杂了, 会遇到4种情况, 实际是8种, 因为其中4种相互对称, 这可以通过判断x是其父结点右孩子还是左孩子区分. 下面我们以x是其父结点的左孩子的情况来分析这4种情况. 实际接下来的调整过程, 就是要想方设法将经过x的所有路径上的黑结数增1.

1) x 的兄弟w是红色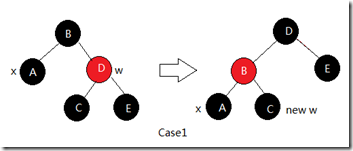 
1-10
这种情况下我们改变w和x的父亲结点颜色,再对x的父亲结点和w之间做一次左旋, 此时x的新兄弟指向旋转之前w的某个孩子．但还不算完, 只是暂时将情况1转变成了情况2, 3, 4.

2) x的兄弟w是黑色,且w的两个孩子都是黑色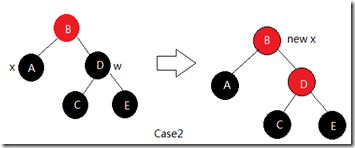  
1-11
在这种情况下我们翻传w的颜色, 将x指针向上移一层. 此时如果以前x的父结点是红的, 如上图, 我们将x上移一层后, x变成指向红结点, 还记得前面讲过, 如果x为红结点则将它直接翻转为黑结点吗?没错, 这里有一个出口, 在遇到x指向红结点时调整将结束, 我们在调整结束时又将x设为黑结点, 因此相当于在经过新x结点的所有路径上黑结点数增加了1, 此时由于原w结点是黑的, w的路径上就多了一个黑色结点, 所以我们将它翻转为红. 注意如果新x结点指向的是黑结点, 则还要以新x结点为参考进行下一次调整.

3) x的兄弟w是黑色, 且w的左孩子是红色, 右孩子是黑色的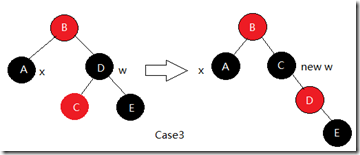 
1-13
情况3中的操作是交换w和其左孩子的颜色, 并对w和其左孩子进行右旋. 于是情况3马上变成了情况4.

4) x的兄弟w是黑色, 且w的右孩子是红色的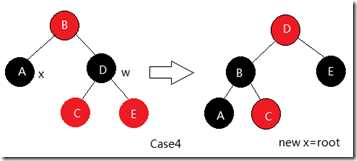 
1-14
在情况4中我们要设置反转w的颜色为红色, 并对w的父结点和x做一次左旋, 旋转后w的两个子结点也要跟着反转成黑色. 此时我们看到原x的路径上黑结点数增加了1, 而其它路径黑结点数不变. 所以我们将x指向根结点, 并结束调整过程.

从上面来看情况1可以转变成情况2,3, 4, 情况3可转变为情况4, 调整过程在遇到情况4时结束. 当遇到情况2时,其指针x沿树上升至多O(logN)次, 但不需要执行任何旋转. 虽然调整过程效复杂,但最多也只花O(logN)次. 代码如下:

void RBTDeleteFixup(Position x) 
{ 
    Position w; 
    while (x != RootNode && x->color == BLACK) { 
        if (x == x->parent->left) { 
            w = x->parent->right; 
            /* Case1 */ 
            if (w->color == RED) { 
                w->color = BLACK; 
                x->parent->color = RED; 
                LeftRotate(x->parent); 
                w = x->parent->right; 
            } 
           /* Case2 */ 
            if (w->left->color == BLACK && w->right->color == BLACK) { 
                w->color = RED; 
                x = x->parent; 
            } else { 
                /* Case 3 */ 
                if (w->right->color == BLACK) { 
                    w->left->color = BLACK; 
                    w->color = RED; 
                    RightRotate( w ); 
                    w = x->parent->right; 
                } 
                /* Case 4 */ 
                w->color = x->parent->color; 
                x->parent->color = BLACK; 
                w->right->color = BLACK; 
                LeftRotate( x->parent ); 
                x = RootNode; 
            } 
        } else { 
            /* 处理x是右孩子的情况, 与上面的代码对称 */ 
        } 
    } 
    x->color = BLACK; 
} 

Postion RBTDelete( z ) 
{ 
     Postion y, x; 
     if (z->left == NullNode || z->right == NullNode)  
          y = z; 
      else  
          y = TreeSuccessor( z ); 
     
    if (y->left != NullNode) 
         x = y->left; 
    else 
         x = y->right; 

    x->parent = y->parent; 
    if (y->parent == NullNode) 
        RootNode = x; 
    else if (y == y->parent->left) 
         y->parent->left = x; 
    else 
         y->parent->right = x; 

    if (y != z) 
        z->element = y->element; 

    if (y->color == BLACK) 
        RBTDeleteFixup( x ); 

    return y; 
} 

RBTDelete的代码与BST的删除代码基本相同, 唯一不同是在y结点为黑时要触发修正过程. 另外结点x的父指针总是指向被删除结点的父结点, 既使x为空结点也没有问题, 因为空结点的父指针在我们的代码中没有定义. TreeSuccessor函数获取某结点的后继, 代码如下:

Position TreeMinimum(Position x) 
{ 
    while (x->left != NullNode) 
       x = x->left; 
    return x; 
} 

Position TreeSuccessor(Position x) 
{ 
    Position y; 
    if (x->right != NullNode) 
        return TreeMinimum(x->right); 

    y = x->parent; 
    while (y != NullNode && x == y->right) { 
        x = y; 
        y = y->parent; 
    } 
    return y; 
}

总结

本文中我仅仅介绍了红黑树的插入删除操作, 由于红黑树的其它操作与普通BST的操作相同, 所以这里没有作讨论. 在红黑树的插入和删除中我采用非递归的方法, 使用自下往上的平衡过程. 你也可以使用自上往下的平衡的办法来实现, 两种方法都差不多复杂. 并且在本文中我把重点放在描述平衡过程, 对平衡步骤未加证明. 有兴趣的同学可以参考<算法导论>.  实际上除了AVL树和红黑树以外还有一些其它一些平衡树, 如AA树, treap树和kd树等. 这里只是希望通过本文对大家理解红黑树这种数据结构有所帮助. 水平有限, 欢迎大家指



http://www.ppmy.cn/news/283250.html

相关文章

红与黑棋盘

红与黑棋盘

import java.util.ArrayList; import java.util.Scanner;public class 红与黑 {static int co0;static ArrayList<char[]> listnew ArrayList<>();public static void main(String[] args) {Scanner scnew Scanner(System.in);int x0,y0;//记录初始位置//初始化whi…
阅读更多...
【硬核】梦回小霸王

【硬核】梦回小霸王

长大&#xff0c;是一个不断失去的过程。 笔者是一位90后。 小时候大家家里条件都差&#xff0c;娱乐手段十分贫乏。不像现在的小孩子可以玩到手机&#xff0c;平板和电脑&#xff0c;那时&#xff0c;一叠小浣熊水浒卡就能玩上一整天&#xff0c;要是有一张稀有卡&#xff0c…
阅读更多...
红军vs蓝军

红军vs蓝军

http://blogs.microsoft.com/cybertrust/2015/10/08/cloud-security-controls-series-penetration-testing-red-teaming-forensics/
阅读更多...
弘辽科技：淘宝卖家打造爆款商品的六大技巧！

弘辽科技：淘宝卖家打造爆款商品的六大技巧！

原标题《弘辽科技&#xff1a;淘宝卖家打造爆款商品的六大技巧&#xff01;》 淘宝商家对于打造爆款很是重视&#xff0c;因为成功打造爆款好处多多&#xff0c;可以给店铺带来流量&#xff0c;可以提升店铺权重和排名&#xff0c;以及带动店铺内其他商品的销量。那么淘宝商家…
阅读更多...
手撕红黑树（Red-Black Tree）

手撕红黑树（Red-Black Tree）

文章目录 ⏰1.相关概念&#x1f384;红黑树的定义&#x1f384;红黑树的性质&#x1f384;红黑树与AVL树的比较 ⏰2.红黑树的实现&#x1f4d5;红黑树的结点定义&#x1f4d5;红黑树的结构&#x1f4d5;红黑树的插入(important!!!)&#x1f315;1、寻找要插入的位置&#x1f31…
阅读更多...
红蓝军对抗

红蓝军对抗

一道智力题&#xff1a;有五个人进行对抗比赛&#xff0c;每次对抗一部分人当红军&#xff0c;一部分人当蓝军。问&#xff0c;至少经过多少次对抗&#xff0c;五个人中的任意两个人都进行过一次红蓝对抗和蓝红对抗&#xff1f; 为满足题意&#xff0c;至少需要出现10种一对一对…
阅读更多...
弘辽科技：电商壹周大事

弘辽科技：电商壹周大事

派代【一周大事】盘点&#xff0c;来了。 刘强东卸任京东集团CEO&#xff0c;将把更多精力投入到战略决策和人才培养上&#xff1b;蒋凡卸任淘宝、天猫法定代表人及董事长&#xff1b;华为支付上线&#xff0c;支持绑定160余家银行&#xff0c;微信、支付宝迎来新对手…… 行业…
阅读更多...
小杨哥陷入打假风波，会变成下一个辛巴吗？

小杨哥陷入打假风波，会变成下一个辛巴吗？

最近&#xff0c;网红疯狂小杨哥频繁登上热搜。最初的起因是他花了1亿元在合肥一家高科技公司购买了5万多平方米的房产&#xff0c;作为他名下公司的全球总部&#xff0c;由此带来了争议。 据了解&#xff0c;该物业总建筑面积为53874.33平方米&#xff0c;包括1个生产综合体、…
阅读更多...
最新文章

Copyright @ 2022~2023