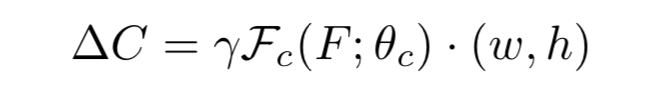文章目录
- 摘要
- 引言
- 方法
- 人脸样本类内-类间相似度分布为何与人脸图像质量高度相关?
- 如何生成质量分数伪标签?
- 质量回归网络

参考链接
摘要
- 近年来,为了保证在无约束场景下识别性能的稳定性和可靠性,人脸图像质量评估(FIQA)已经成为人脸识别系统不可或缺的一部分。为此,FIQA方法需要同时考虑人脸图像的内在属性和可识别性。以往的研究大多以估计样本嵌入不确定性或两两相似度作为质量分数,而只考虑部分类内信息。但是,这些方法忽略了来自类间的有价值的信息,这是对人脸图像可识别性的估计。
- 在这项工作中,我们认为高质量的人脸图像应该与其类内样本相似,而与其类间样本不同。因此,我们提出了一种新的无监督的FIQA方法,该方法融合了人脸图像质量评估的相似分布距离(SDD-FIQA)。该方法通过计算类内相似度分布和类间相似度分布之间的Wasserstein距离(WD)来生成高质量的伪标签。利用这些质量伪标签,我们可以训练一个回归网络来进行质量预测。
引言
- 人脸识别是生物特征识别研究的热点领域之一。在受控条件下,该识别系统通常能达到令人满意的性能。然而,在一些实际应用中,识别系统需要在不受约束的环境下工作(如监控摄像头和户外场景),导致识别精度显著下降,识别性能不稳定。许多研究人员在提高不同条件下的识别精度方面取得了进展,但有时仍然会受到姿态、光照、遮挡等不可预测的环境因素的影响。为了保持人脸识别系统的性能稳定可靠,人脸图像质量评估(FIQA)技术应运而生,支持识别系统选择高质量的图像或丢弃低质量的图像以获得稳定的识别性能。
- 现有的FIQA方法大致可以分为两类:基于分析的和基于学习的。基于分析的FIQA通过人类视觉系统(HVS)定义质量指标,并通过手工制作的特征评估面部图像质量,比如人脸不对称特征、光照强度、垂直边缘密度。然而,这些方法必须手动提取不同质量退化的特征,手动注释所有可能的退化是不现实的。因此,更多的研究人员将精力投入到基于学习的方法中,人脸识别效果直接决定质量分数(如FaceQnet)。这些方法中最关键的部分是建立图像质量与识别模型之间的映射函数。
- Aggarwal等人[1]提出了一种多维尺度方法,将空间表征特征映射到真正的质量分数。Hernandez-Ortega et al.[10]计算类内识别嵌入的欧氏距离作为质量评分。Shi等人[23]和Terhorst等人[25]提出了预测识别嵌入随人脸图像质量变化的方法。最近,Xie等人[29]提出PCNet通过动态挖掘正匹配对来评估人脸图像质量。尽管这些基于学习的方法在FIQA方面取得了进展,但性能仍然不理想。由于它们从识别模型中只考虑了部分类内相似性或特征不确定性,而忽略了类间相似性的重要信息,这是影响人脸图像可识别性的关键因素。
- 在本文中,我们提出了一种新的基于学习的方法,称为SDD-FIQA。将FIQA视为一个可识别性估计问题,首先揭示了识别性能与人脸图像质量之间的内在关系。针对目标样本,我们采用识别模型收集其类内相似度分布(Pos-Sim)和类间相似度分布(negi - sim)。然后计算这两个分布之间的Wasserstein距离(WD)作为质量伪标记。最后,在Huber损失的约束下训练出一个质量回归网络。该方法可以在无标签的情况下准确预测人脸图像质量分数。
方法
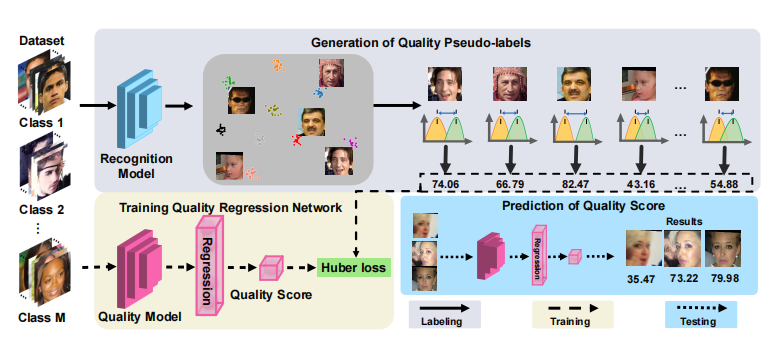
Step1:将训练数据遍历人脸识别模型,采集对应的类内分布和类间分布;
Step2:计算类内分布和类间分布的Wasserstein距离,并作为质量分数伪标签;
Step3:在Huber loss的约束下训练质量分数回归网络。
人脸样本类内-类间相似度分布为何与人脸图像质量高度相关?
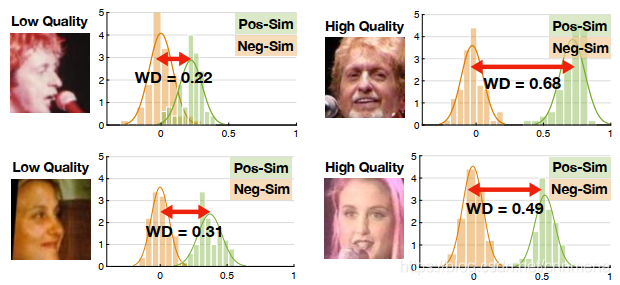
从人脸识别效果来看,一张高质量的人脸图像更容易被识别正确,这表示它与类内的相似性距离较近,与其它类间的相似性距离较远。换句话来说,它的类内相似性分布与类间相似性分布距离较远。图像质量与类内-类间相似度距离如下图所示,低质量人脸WD距离较近,高质量人脸WD距离较远。
另外,文中根据EVRC(Error Versus Reject Curve)曲线从理论上推导了质量分数与识别性能的关系。
如何生成质量分数伪标签?
SDD-FIQA综合考虑了目标样本的与类内样本和类间样本的相似性,类内样本与类间样本的分布距离结果作为质量伪标签,作者使用WD(Wasserstein Distance)计算类内与类间的分布距离。
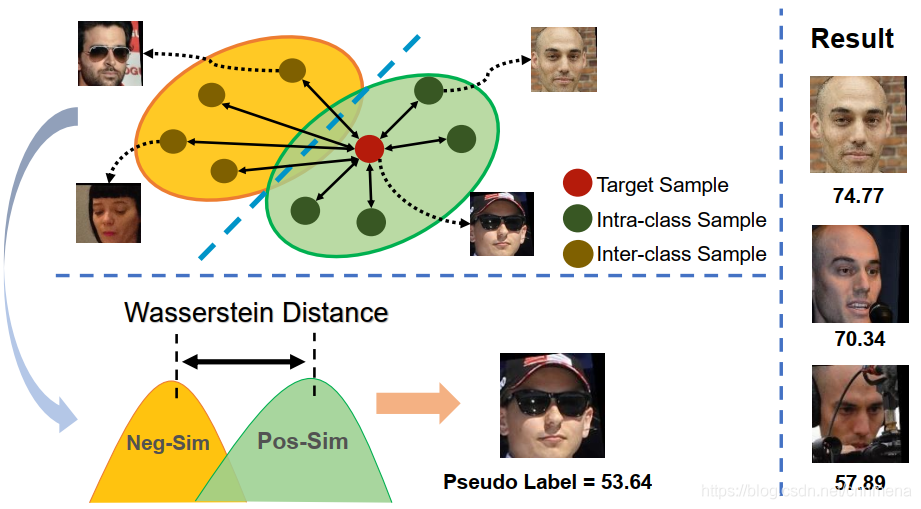
图中红点表示目标样本,绿点表示类内样本,黄点表示类间样本。类内相似性分布(Pos-Sim)与类间相似性分布(Neg-Sim)的WD距离为质量分数伪标签,质量分数结果如图中右侧所示。
假设X,Y,F分别表示图片集、id标签集、识别特征集,构建一个三元组数据集

质量回归网络
为了使质量回归网络的预测结果与识别系统相匹配,在训练过程中应用知识转移。具体来说,我们首先从预先训练的人脸识别模型中去除嵌入层和分类层。然后我们使用0.5概率的dropout算子来避免训练过程中过拟合,并添加一个全连接层来输出FIQA的质量分数。最后,利用Huber损失函数对质量回归网络进行训练。相比MSE,Huber损失对数据中异常值更具鲁棒性。