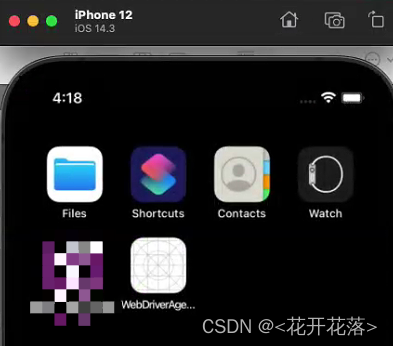
1，利用类来构建结点，利用函数递归来构建树

2，因为左子树的结点编号是父节点的2倍，右子树的结点编号是父节点的2倍+1，所以可以用数组模拟建树的过程

构建二叉树

第一种构建方式

class treenode():#二叉树节点def __init__(self,val,lchild=None,rchild=None):self.val=val        #二叉树的节点值self.lchild=lchild        #左孩子self.rchild=rchild        #右孩子def creat_tree(root,vals):if len(vals)==0:#终止条件：val用完了return rootif vals[0]!='#':#本层需要干的就是构建root、root.lchild、root.rchild三个节点。root = treenode(vals[0])vals.pop(0)root.lchild = creat_tree(root.lchild,val)root.rchild = creat_tree(root.rchild,val)return root#本次递归要返回给上一次的本层构造好的树的根节点else:root=Nonevals.pop(0)return root#本次递归要返回给上一次的本层构造好的树的根节点if __name__ == '__main__':root = Nonestrs="abc##d##e##"#前序遍历扩展的二叉树序列vals = list(strs)roots=creat_tree(root,vals)#roots就是我们要的二叉树的根节点。

第二种构建方式

#存储结构的创建
class node:def __init__(self,data):self.data=data#数据域self.left=None#指向左子树根节点的指针self.right=None#指向右子树根节点的指针
root=None#如果根节点不存在l=[1,2,None,3,5,2,1]#假设题目给出列表形式的二叉树各节点数据
def newNode(input_list=[]):#创建二叉树，即二叉树插入if input_list is None or len(input_list)==0:#如果列表为空return Nonedata=input_list.pop(0)#取出并删除“当前”列表第一个数据if data is None:#到达空树，递归边界return Noneroot=node(data)#将该数据设置为根节点的数据，并创建此根节点的存储地址。root.left=newNode(input_list)#该根节点的左节点为“当前”列表的第二个数据root.right=newNode(input_list)#该根节点的右节点为“当前”列表的第三个数据#左右节点的递归顺序要根据题目给出的前中后层序排序改变。当前为前序遍历插入#中序遍历插入# root.left=newNode(input_list)# root = node(data)# root.right=newNode(input_list)#后序遍历插入# root.left=newNode(input_list)# root.right=newNode(input_list)# root=node(data)#层序遍历插入return root
newNode(l)

二叉树的四种遍历

#二叉树遍历
#前序遍历
#root是构建二叉树后得到的根结点
def preorder(root):if root==None:return#到达空树，递归边界print(root.data)#访问根节点preorder(root.left)#访问左子树preorder(root.right)#访问右子树
#中序遍历
def inorder(root):if root==None:return#到达空树，递归边界inorder(root.left)  # 访问左子树print(root.data)#访问根节点inorder(root.right)#访问右子树
#后序遍历
def postorder(root):if root==None:return#到达空树，递归边界postorder(root.left)#访问左子树postorder(root.right)#访问右子树print(root.data)  # 访问根节点
#层序遍历
from queue import Queue
def layerorder(root):q=Queue()#注意队列里是存地址q.put(root)#将根节点地址入队while not q.empty():newroot=q.get()#取出队首元素q.pop()print(newroot.data)#访问队首元素if newroot.left is not None:#左子树非空q.put(newroot.left)if newroot.right is not None:#右子树非空q.put(newroot.right)#二叉树结点的查找,修改
goaldata=10#目标数据
newdata=11#新的数据
def search(root,goaldata,newdata):#先传进根节点if root==None:returnif root.data==goaldata:root.data=newdata# 再依次传进左右子节点search(root.left,goaldata,newdata)#往左子树搜索xsearch(root.right,goaldata,newdata)#往右子树搜素x

二叉树题目其一：已知两种遍历求其他所有遍历

结论:中序序列可以与先序序列、后序序列、层序序列中的任意一个来构建唯一的二叉树，而后三者两两搭配或是三个一起上都无法构建唯一的二叉树。原因是先序、后序、层序均是提供根结点,作用是相同的,都必须由中序序列来区分出左右子树。

L2-006 树的遍历

已知中后求层序

class node:def __init__(self,data):self.data=dataself.left=Noneself.right=Nonen=int(input())
l1=list(map(int,input().split()))
l2=list(map(int,input().split()))def buildTree(inorder,postorder):def helper(in_left,in_right):if in_left>in_right:return Nonedata=postorder.pop()#后序排序从后依次弹出，遵循根右左，故一开始是根，之后一直右，然后左，如何判断该节点是左右，只需看in_left>in_right即可，一旦in_left<=in_right，说明右已经没有，开始进行左。root=node(data)index=idx_map[data]root.right = helper(index + 1, in_right)#为什么root.right必须放在root.left上面，在data是按后序排序逆序弹出#弹出根节点后就弹出右节点，这个时候如果先遍历左子树会找不到左子树的根节点root.left=helper(in_left,index-1)return rootidx_map={val:idx for idx,val in enumerate(inorder)}#将中序列表的值和下标对应return helper(0,len(inorder)-1)
p=buildTree(l2,l1)#得到的是一堆root数据结构的首地址，也就是二叉树根节点的地址
# print(p)
q=[p]#将首地址放到列表结构中
# print(q.pop(0))
res=[]
while(len(q)!=0):m=q.pop(0)#取出首地址if m!=None:res.append(m.data)if m.left!=None:q.append(m.left)if m.right!=None:q.append(m.right)
print(*res)

L2-011 玩转二叉树

已知前中镜像翻转后求层

前序遍历倒过来就是后序遍历的镜像

from queue import Queue
n=int(input())
zx=list(map(int,input().split()))
qx=list(map(int,input().split()))class node():def __init__(self,data):self.data=dataself.left=Noneself.right=None
idx_map={val:i for i,val in enumerate(zx)}
def coms(inl,inr):if inl>inr:return Nonedata=qx.pop(0)#在前序中找到根节点#前序排序从前依次弹出，遵循根左右，故一开始是根，之后一直左，然后左，如何判断该节点是左右，只需看in_left>in_right即可，一旦in_left<=in_right，说明左已经没有，开始进行右。index=idx_map[data]#利用根节点的值找到其下标root=node(data)#建立二叉树#再利用下标将其分开#l.append(data)前序遍历root.left = coms(inl, index - 1)#l.append(data)中序遍历root.right = coms(index + 1, inr)# l.append(data)后序遍历return rootp=coms(0,len(zx)-1)#得到的是一堆root数据结构的首地址，也就是二叉树根节点的地址
# print(p)
q=[p]#将首地址放到列表结构中
# print(q.pop(0))
res=[]
while(len(q)!=0):m=q.pop(0)#取出首地址if m!=None:res.append(m.data)if m.right!=None:q.append(m.right)if m.left!=None:q.append(m.left)
print(*res)

from queue import Queue
n=int(input())
zx=list(map(int,input().split()))
qx=list(map(int,input().split()))class node():def __init__(self,data):self.data=dataself.left=Noneself.right=None
idx_map={val:i for i,val in enumerate(zx)}
def coms(inl,inr):if inl>inr:return Nonedata=qx.pop(0)#在前序中找到根节点index=idx_map[data]#利用根节点的值找到其下标root=node(data)#建立二叉树#再利用下标将其分开#l.append(data)前序遍历root.left = coms(inl, index - 1)#l.append(data)中序遍历root.right = coms(index + 1, inr)# l.append(data)后序遍历return root
l=[]
def level(node):queue=Queue()queue.put(node)while not queue.empty():node=queue.get()l.append(node.data)if node.right is not None:#先加入右节点，做镜像翻转queue.put(node.right)if node.left is not None:queue.put(node.left)
level(coms(0,len(zx)-1))
print(*l)

L2-035 完全二叉树的层序遍历

由于树是递归实现的，后序排序符合递归顺序，而层序排序的顺序可以为我们提供每一次递归所满足的代数式。

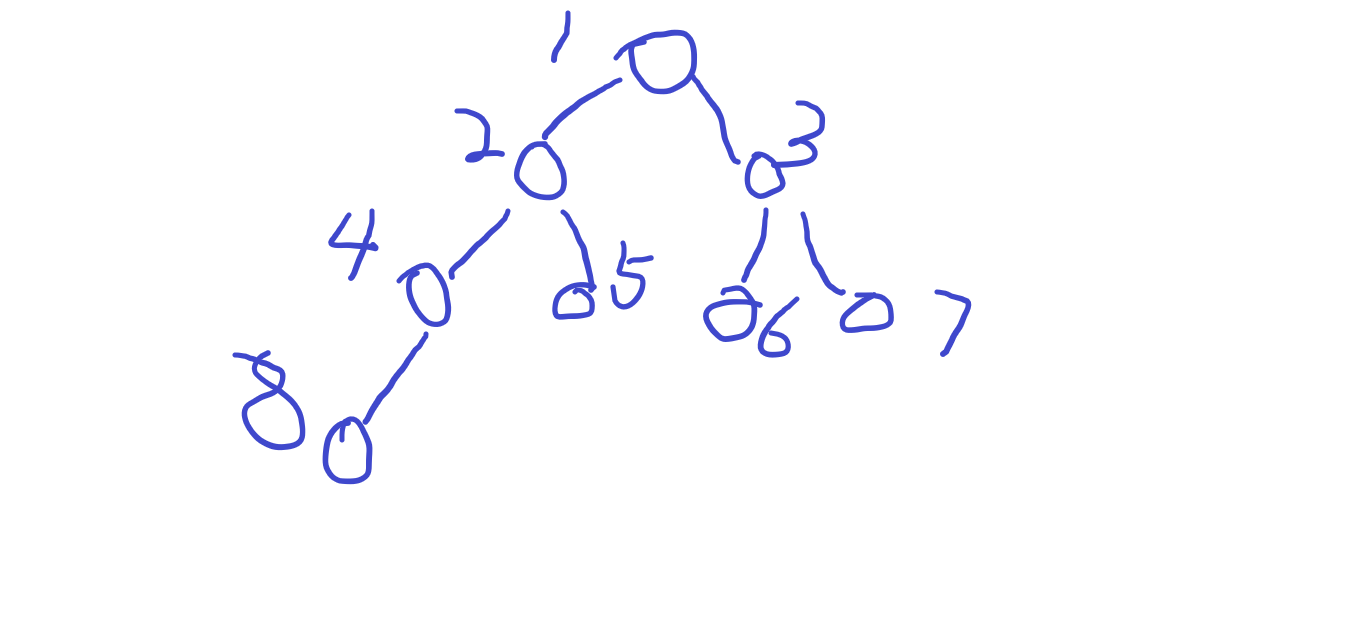
n=int(input())
l=list(map(int,input().split()))
tree=[0]*n
def dfs(x):global indexif x>n:returndfs(x*2)dfs(x*2+1)tree[x-1]=l[index]index+=1
index=0
dfs(1)
print(*tree)

二叉搜素树(BST)

二叉查找树一个实用的性质：对二叉查找树进行中序遍历，遍历的结果是有序的。

这是由于二叉查找树本身的定义中就包含了左子树<根结点<右子树的特点，而中序遍历的访问顺序也是左子树→根结点→右子树,因此,所得到的中序遍历序列是有序的。

# -*- coding:utf-8 -*-import sysreload(sys)
sys.setdefaultencoding('utf-8')class BSTNode:"""定义一个二叉树节点类。以讨论算法为主，忽略了一些诸如对数据类型进行判断的问题。"""def __init__(self, data, left=None, right=None):"""初始化:param data: 节点储存的数据:param left: 节点左子树:param right: 节点右子树"""self.data = dataself.left = leftself.right = rightclass BinarySortTree:"""基于BSTNode类的二叉排序树。维护一个根节点的指针。"""def __init__(self):self._root = Nonedef is_empty(self):return self._root is Nonedef search(self, key):"""关键码检索:param key: 关键码:return: 查询节点或None"""bt = self._rootwhile bt:entry = bt.dataif key < entry:bt = bt.leftelif key > entry:bt = bt.rightelse:return entryreturn Nonedef insert(self, key):"""插入操作:param key:关键码:return: 布尔值"""if self.is_empty():self._root = BSTNode(key)bt = self._rootwhile True:entry = bt.dataif key < entry:if bt.left is None:bt.left = BSTNode(key)bt = bt.leftelif key > entry:if bt.right is None:bt.right = BSTNode(key)bt = bt.rightelse:bt.data = keyreturndef delete(self, key):"""二叉排序树最复杂的方法:param key: 关键码:return: 布尔值"""p, q = None, self._root # 维持p为q的父节点，用于后面的链接操作if not q:print("空树！")returnwhile q and q.data != key:p = qif key < q.data:q = q.leftelse:q = q.rightif not q: # 当树中没有关键码key时，结束退出。return# 上面已将找到了要删除的节点，用q引用。而p则是q的父节点或者None（q为根节点时）。if not q.left:if p is None:self._root = q.rightelif q is p.left:p.left = q.rightelse:p.right = q.rightreturn# 查找节点q的左子树的最右节点，将q的右子树链接为该节点的右子树# 该方法可能会增大树的深度，效率并不算高。可以设计其它的方法。r = q.leftwhile r.right:r = r.rightr.right = q.rightif p is None:self._root = q.leftelif p.left is q:p.left = q.leftelse:p.right = q.leftdef _pre_order(self, node=None):if node is None:node = self._rootyield node.dataif node.left is not None:for item in self._pre_order(node.left):yield itemif node.right is not None:for item in self._pre_order(node.right):yield itemdef _mid_order(self, node=None):if node is None:node = self._rootif node.left is not None:for item in self._mid_order(node.left):yield itemyield node.dataif node.right is not None:for item in self._mid_order(node.right):yield itemdef _mid_order1(self):"""实现二叉树的中序遍历算法,展示我们创建的二叉排序树.直接使用python内置的列表作为一个栈。:return: data"""stack = []node = self._rootwhile node or stack:while node:stack.append(node)node = node.leftnode = stack.pop()yield node.datanode = node.rightdef _post_order(self, node=None):if node is None:node = self._rootif node.left is not None:for item in self._post_order(node.left):yield itemif node.right is not None:for item in self._post_order(node.right):yield itemyield node.datadef pre_order(self):return list(self._pre_order())def mid_order(self):return list(self._mid_order()) # return list(self._mid_order1())def post_order(self):return list(self._post_order())if __name__ == '__main__':lis = [62, 58, 88, 47, 73, 99, 35, 51, 93, 37]bs_tree = BinarySortTree()for i in range(len(lis)):bs_tree.insert(lis[i])print "先序遍历：", bs_tree.pre_order()print "中序遍历：", bs_tree.mid_order()print "后序遍历：", bs_tree.post_order()

L3-010 是否完全二叉搜索树

因为左子树的结点编号是父节点的2倍，右子树的结点编号是父节点的2倍+1，所以可以用数组模拟建树的过程;

最后题目要求层序输出比较简单，直接按编号大小输出即可;

还有一问是判断该树是否为完全二叉树，完全二叉树的定义是若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，所以最后的结点编号肯定和n是相等的。

平衡二叉树

并查集

路径压缩

哈夫曼树