目录
1.电机模型
2.数字PID控制
3.MATLAB数字仿真分析
3.1matlab程序
3.2 仿真结果
4. SIMULINK仿真分析
4.1simulink模型
4.2仿真结果
4.3 小结
1.电机模型
即:
其中:J = 0.0067;B = 0.10
2.数字PID控制
首先我们来看一下连续PID:
![]()

简单说来,PID控制器各校正环节的作用如下:
(1)比例环节:成比例地反映控制系统的偏差信号error(t),偏差一旦产生,控制器立即产生控制作用,以减少偏差。
(2)积分环节:主要用于消除静差,提高系统的无差度。积分作用的强弱取决于积分时间常数T,T越大,积分作用越弱,反之则越强。
(3)微分环节:反映偏差信号的变化趋势(变化速率),并能在偏差信号变得太大之前,在系统中引入一个有效的早期修正信号,从而加快系统的动作速度,减少调节时间。
按模拟PID控制算法,以一系列的采样时刻点kT代表连续时间t,以矩形法数值积分近似代替积分,以一阶后向差分近似代替微分,即:

3.MATLAB数字仿真分析
3.1matlab程序
主程序:
clear all
clc;
xk = zeros(2,1);%定义初始状态
ts = 0.001;
e_1 = 0;
u_1 = 0;
for k = 1:2000 %仿真时间=k*tstime(k)= k*ts;xd(k) = 0.5*sin(2*pi*k*ts);%跟踪位移信号,即x1跟踪xdtspan = [(k-1)*ts k*ts];%当前时刻求解的积分区间para = u_1;%控制输入[tt,x] = ode45('Plant',tspan,xk,[],para);xk = x(length(x),:);%取求解向量的最后一行,且作为下一时刻的初始状态x1(k) = xk(1);%选位移信息作为输出向量e(k) = xd(k)-x1(k);%误差比例 de(k) = (e(k)-e_1)/ts;%误差微分P = 20;D = 0.5;u(k) = P*e(k)+D*de(k);u_1 = u(k);%更新当前时刻的控制输入e_1 = e(k);%更新当前时刻的跟踪误差
end
figure(1)
plot(time,x1,'k',time,xd,'r','linewidth',1)
legend('x1','xd')
xlabel('t');ylabel('x1(转速)')
figure(2)
plot(time,u,'k','linewidth',1)
xlabel('t');ylabel('PD控制输入')
figure(3)
plot(time,e,'k','linewidth',1)
xlabel('t');ylabel('跟踪误差e')
figure(4)
plot(time,de,'k','linewidth',1)
xlabel('t');ylabel('跟踪误差变化率de')
% function dx = Plant(tspan,x,flag,para)
% u = para;
% J = 0.0067;B = 0.1;
% dx = zeros(2,1);%注意要将状态变量定位列向量,否则系统默认为行向量
% dx(1) = x(2);
% dx(2) = -(B/J)*x(2)+u/J;
% end电机模型:
function dx = Plant(tspan,x,flag,para)
% tspan:积分时间段、x当前求解微分方程时刻的初始状态、para:当前时刻的控制输入
u = para;
J = 0.0067;B = 0.1;
dx = zeros(2,1);%注意要将状态变量定位列向量,否则系统默认为行向量
dx(1) = x(2);
dx(2) = -(B/J)*x(2)+u/J;
end3.2 仿真结果




4. SIMULINK仿真分析
对比一下纯数字仿真和simulink建模仿真:连续PID、离散PID模块、离散PID S函数3种仿真效果对比:
4.1simulink模型

4.2仿真结果


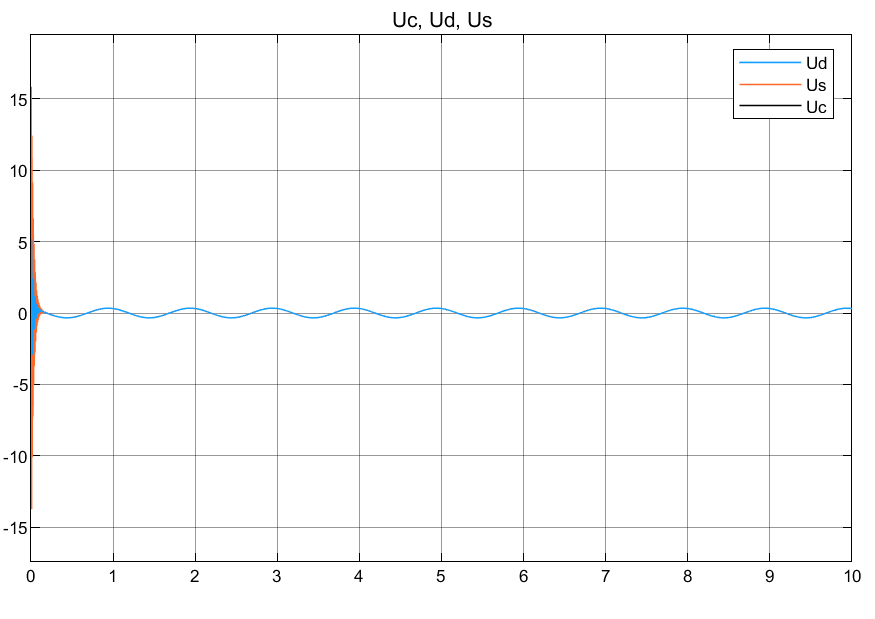
4.3 小结
可以看到还是有细小的差异,但是离散PD模块为什么和离散s函数编写的PD控制器控制输入有差异呢?是因为内部离散PD模块的原因么?