通常,Logistic回归用于二分类问题,例如预测明天是否会下雨。当然它也可以用于多分类问题.
Logistic回归是分类方法,它利用的是Sigmoid函数阈值在[0,1]这个特性。Logistic回归进行分类的主要思想是:根据现有数据对分类边界线建立回归公式,以此进行分类。其实,Logistic本质上是一个基于条件概率的判别模型(Discriminative Model)。
所以要想了解Logistic回归,我们必须先看一看Sigmoid函数 ,我们也可以称它为Logistic函数。它的公式如下:
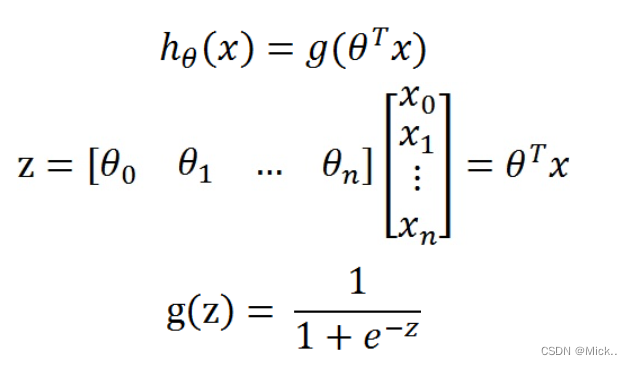
整合成一个公式,就变成了如下公式
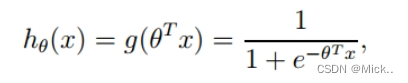
θ是参数列向量(要求解的),x是样本列向量(给定的数据集).这样我们的数据集([x0,x1,...,xn]),不管是大于1或者小于0,都可以映射到[0,1]区间进行分类。hθ(x)给出了输出为1的概率
那么问题来了!如何得到合适的参数向量θ?

式即为在已知样本x和参数θ的情况下,样本x属于正样本(y=1)和负样本(y=0)的条件概率。理想状态下,根据上述公式,求出各个点的概率均为1,也就是完全分类都正确。但是考虑到实际情况,样本点的概率越接近于1,其分类效果越好。比如一个样本属于正样本的概率为0.51,那么我们就可以说明这个样本属于正样本。另一个样本属于正样本的概率为0.99,那么我们也可以说明这个样本属于正样本。但是显然,第二个样本概率更高,更具说服力。我们可以把上述两个概率公式合二为一: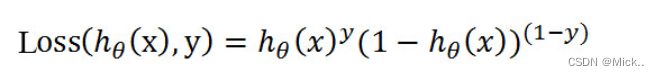
为了简化问题,我们对整个表达式求对数
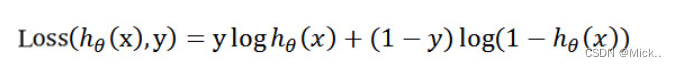
这个损失函数,是对于一个样本而言的。给定一个样本,我们就可以通过这个损失函数求出,样本所属类别的概率,而这个概率越大越好,所以也就是求解这个损失函数的最大值。既然概率出来了,那么最大似然估计也该出场了。假定样本与样本之间相互独立,那么整个样本集生成的概率即为所有样本生成概率的乘积,便可得到如下公式
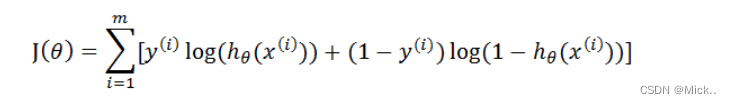
其中,m为样本的总数,y(i)表示第i个样本的类别,x(i)表示第i个样本,需要注意的是θ是多维向量,x(i)也是多维向量。
综上所述,满足J(θ)的最大的θ值即是我们需要求解的模型。
怎么求解使J(θ)最大的θ值呢?因为是求最大值,所以我们需要使用梯度上升算法。如果面对的问题是求解使J(θ)最小的θ值,那么我们就需要使用梯度下降算法。
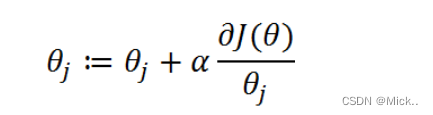
def Gradient_Ascent_test():def f_prime(x_old): # f(x)的导数return -2 * x_old + 4x_old = -1 # 初始值,给一个小于x_new的值x_new = 0 # 梯度上升算法初始值,即从(0,0)开始alpha = 0.01 # 步长,也就是学习速率,控制更新的幅度presision = 0.00000001 # 精度,也就是更新阈值while abs(x_new - x_old) > presision:x_old = x_newx_new = x_old + alpha * f_prime(x_old) # 上面提到的公式print(x_new) # 打印最终求解的极值近似值if __name__ == '__main__':Gradient_Ascent_test()目标函数
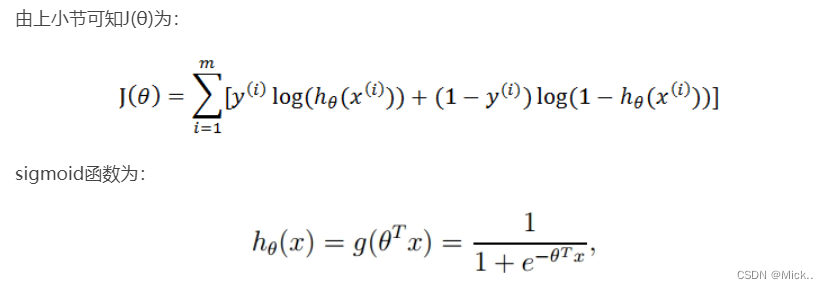


代码
-0.017612 14.053064 0 -1.395634 4.662541 1 -0.752157 6.538620 0 -1.322371 7.152853 0 0.423363 11.054677 0 0.406704 7.067335 1 0.667394 12.741452 0 -2.460150 6.866805 1 0.569411 9.548755 0 -0.026632 10.427743 0 0.850433 6.920334 1 1.347183 13.175500 0 1.176813 3.167020 1 -1.781871 9.097953 0 -0.566606 5.749003 1 0.931635 1.589505 1 -0.024205 6.151823 1 -0.036453 2.690988 1 -0.196949 0.444165 1 1.014459 5.754399 1 1.985298 3.230619 1 -1.693453 -0.557540 1 -0.576525 11.778922 0 -0.346811 -1.678730 1 -2.124484 2.672471 1 1.217916 9.597015 0 -0.733928 9.098687 0 -3.642001 -1.618087 1 0.315985 3.523953 1 1.416614 9.619232 0 -0.386323 3.989286 1 0.556921 8.294984 1 1.224863 11.587360 0 -1.347803 -2.406051 1 1.196604 4.951851 1 0.275221 9.543647 0 0.470575 9.332488 0 -1.889567 9.542662 0 -1.527893 12.150579 0 -1.185247 11.309318 0 -0.445678 3.297303 1
数据可视化
import matplotlib.pyplot as plt
import numpy as np"""
函数说明:加载数据Parameters:无
Returns:dataMat - 数据列表labelMat - 标签列表
"""def loadDataSet():dataMat = [] # 创建数据列表labelMat = [] # 创建标签列表fr = open('testSet.txt') # 打开文件for line in fr.readlines(): # 逐行读取lineArr = line.strip().split() # 去回车,放入列表dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) # 添加数据labelMat.append(int(lineArr[2])) # 添加标签fr.close() # 关闭文件return dataMat, labelMat # 返回"""
函数说明:绘制数据集Parameters:无
Returns:无
"""def plotDataSet():dataMat, labelMat = loadDataSet() # 加载数据集dataArr = np.array(dataMat) # 转换成numpy的array数组n = np.shape(dataMat)[0] # 数据个数xcord1 = [];ycord1 = [] # 正样本xcord2 = [];ycord2 = [] # 负样本for i in range(n): # 根据数据集标签进行分类if int(labelMat[i]) == 1:xcord1.append(dataArr[i, 1]);ycord1.append(dataArr[i, 2]) # 1为正样本else:xcord2.append(dataArr[i, 1]);ycord2.append(dataArr[i, 2]) # 0为负样本fig = plt.figure()ax = fig.add_subplot(111) # 添加subplotax.scatter(xcord1, ycord1, s=20, c='red', marker='s', alpha=.5) # 绘制正样本ax.scatter(xcord2, ycord2, s=20, c='green', alpha=.5) # 绘制负样本plt.title('DataSet') # 绘制titleplt.xlabel('x');plt.ylabel('y') # 绘制labelplt.show() # 显示if __name__ == '__main__':plotDataSet()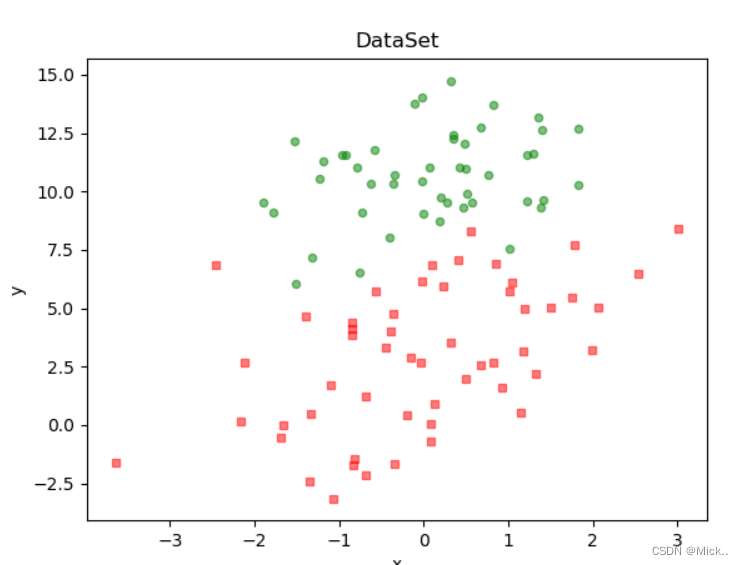

# -*- coding:UTF-8 -*-
import numpy as npdef loadDataSet():dataMat = [] # 创建数据列表labelMat = [] # 创建标签列表fr = open('testSet.txt') # 打开文件for line in fr.readlines(): # 逐行读取lineArr = line.strip().split() # 去回车,放入列表dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) # 添加数据labelMat.append(int(lineArr[2])) # 添加标签fr.close() # 关闭文件return dataMat, labelMat # 返回def sigmoid(inX):return 1.0 / (1 + np.exp(-inX))"""
函数说明:梯度上升算法Parameters:dataMatIn - 数据集classLabels - 数据标签
Returns:weights.getA() - 求得的权重数组(最优参数)
"""def gradAscent(dataMatIn, classLabels):dataMatrix = np.mat(dataMatIn) # 转换成numpy的matlabelMat = np.mat(classLabels).transpose() # 转换成numpy的mat,并进行转置m, n = np.shape(dataMatrix) # 返回dataMatrix的大小。m为行数,n为列数。alpha = 0.001 # 移动步长,也就是学习速率,控制更新的幅度。maxCycles = 500 # 最大迭代次数weights = np.ones((n, 1))for k in range(maxCycles):h = sigmoid(dataMatrix * weights) # 梯度上升矢量化公式error = labelMat - hweights = weights + alpha * dataMatrix.transpose() * errorreturn weights.getA() # 将矩阵转换为数组,返回权重数组if __name__ == '__main__':dataMat, labelMat = loadDataSet()print(gradAscent(dataMat, labelMat)) 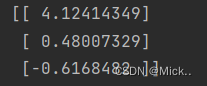
import matplotlib.pyplot as plt
import numpy as np
def loadDataSet():dataMat = [] # 创建数据列表labelMat = [] # 创建标签列表fr = open('testSet.txt') # 打开文件for line in fr.readlines(): # 逐行读取lineArr = line.strip().split() # 去回车,放入列表dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) # 添加数据labelMat.append(int(lineArr[2])) # 添加标签fr.close() # 关闭文件return dataMat, labelMat # 返回def sigmoid(inX):return 1.0 / (1 + np.exp(-inX))def gradAscent(dataMatIn, classLabels):dataMatrix = np.mat(dataMatIn) # 转换成numpy的matlabelMat = np.mat(classLabels).transpose() # 转换成numpy的mat,并进行转置m, n = np.shape(dataMatrix) # 返回dataMatrix的大小。m为行数,n为列数。alpha = 0.001 # 移动步长,也就是学习速率,控制更新的幅度。maxCycles = 500 # 最大迭代次数weights = np.ones((n, 1))for k in range(maxCycles):h = sigmoid(dataMatrix * weights) # 梯度上升矢量化公式error = labelMat - hweights = weights + alpha * dataMatrix.transpose() * errorreturn weights.getA() # 将矩阵转换为数组,返回权重数组def plotBestFit(weights):dataMat, labelMat = loadDataSet() # 加载数据集dataArr = np.array(dataMat) # 转换成numpy的array数组n = np.shape(dataMat)[0] # 数据个数xcord1 = [];ycord1 = [] # 正样本xcord2 = [];ycord2 = [] # 负样本for i in range(n): # 根据数据集标签进行分类if int(labelMat[i]) == 1:xcord1.append(dataArr[i, 1]);ycord1.append(dataArr[i, 2]) # 1为正样本else:xcord2.append(dataArr[i, 1]);ycord2.append(dataArr[i, 2]) # 0为负样本fig = plt.figure()ax = fig.add_subplot(111) # 添加subplotax.scatter(xcord1, ycord1, s=20, c='red', marker='s', alpha=.5) # 绘制正样本ax.scatter(xcord2, ycord2, s=20, c='green', alpha=.5) # 绘制负样本x = np.arange(-3.0, 3.0, 0.1)y = (-weights[0] - weights[1] * x) / weights[2]ax.plot(x, y)plt.title('BestFit') # 绘制titleplt.xlabel('X1');plt.ylabel('X2') # 绘制labelplt.show()if __name__ == '__main__':dataMat, labelMat = loadDataSet()weights = gradAscent(dataMat, labelMat)plotBestFit(weights)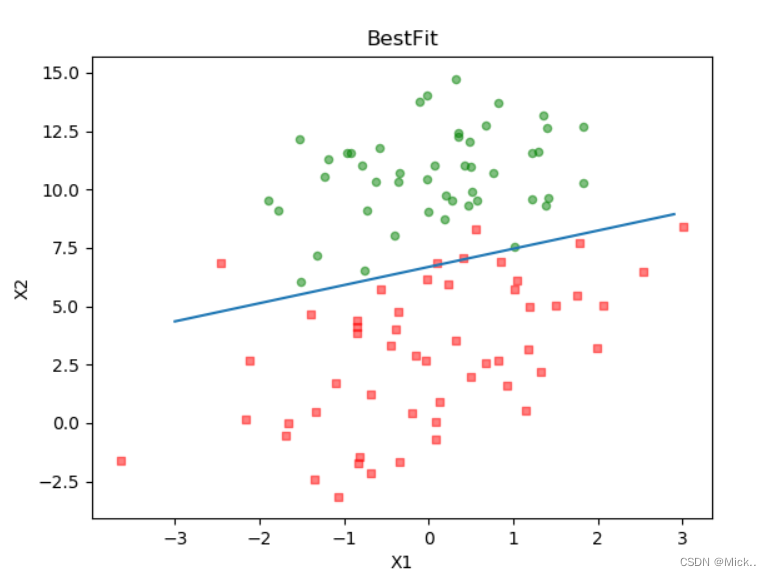
机器学习实战教程(六):Logistic回归基础篇之梯度上升算法 (cuijiahua.com)