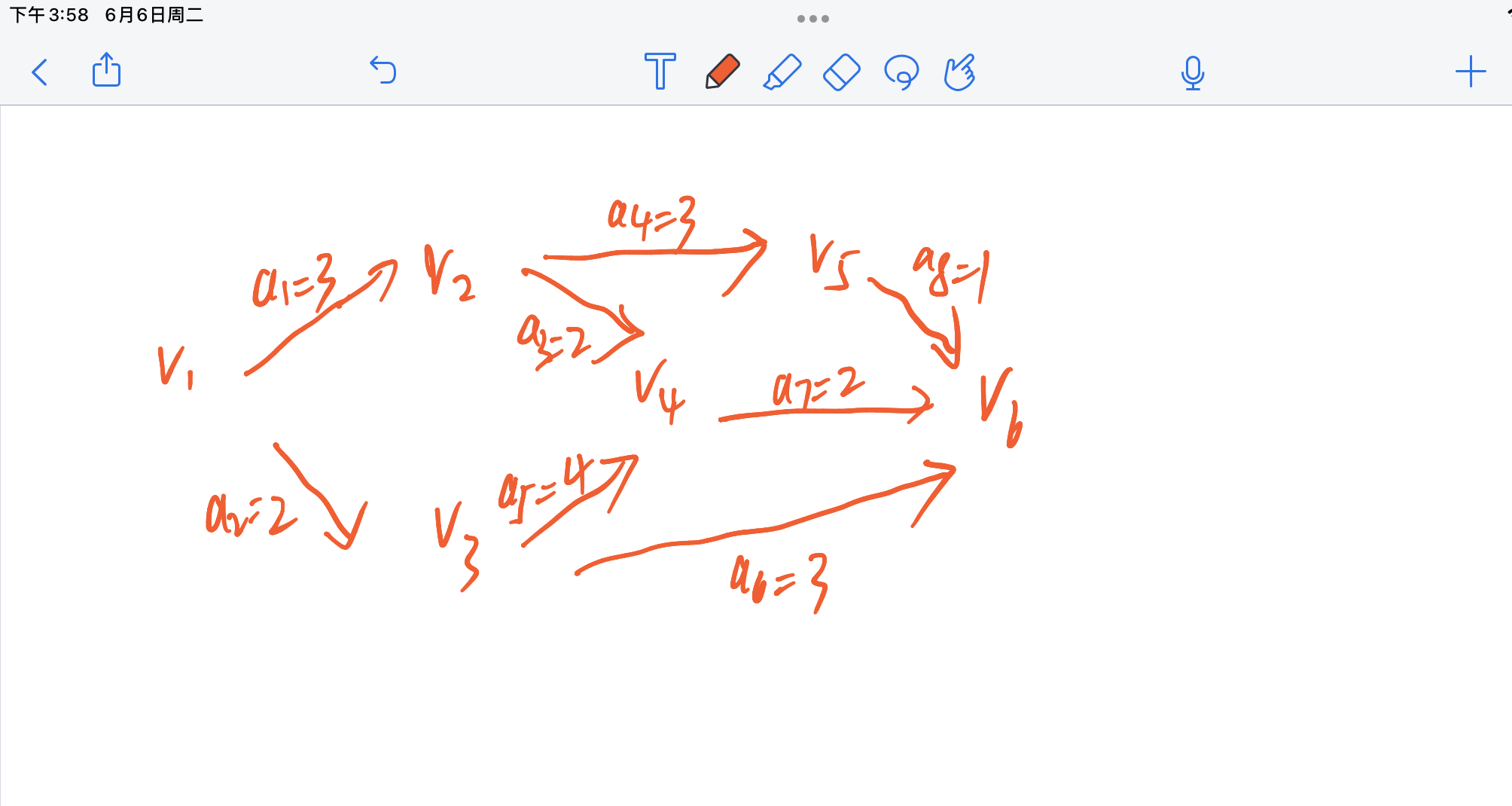
数据结构-图
- 1 知识框架
- 2 图结构的存储
- 2.1 邻接矩阵法
- 2.2 邻接表法
- 2.3 十字链表法
- 2.4 邻接多重表
- 3 图的遍历
- 3.1 dfs(深度优先遍历)
- 3.2 bfs(广度优先遍历)
- 4 最小生成树
- 4.1 Prim
- 4.2 kruskal
- 5 最短路径
- 5.1 Dijkstra
- 5.2 Floyd
- 6 AOV网和AOE网
- 6.1 AOV
- 6.2 AOE
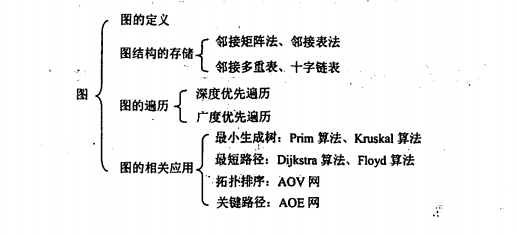
1 知识框架
完全图:
1.无向完全图:任意两个顶点之间存在边
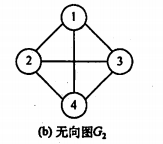
2.有向完全图:任意两个顶点之间都存在方向相反的两条弧,则为有向完全图。
又称这一对顶点是强连通的,图中任意一对顶点都是强连通的则称此图为强连通图,其中极大强连通子图称为强连通分量。
2 图结构的存储
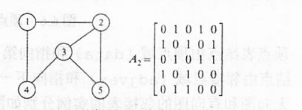
2.1 邻接矩阵法
用二维数组表示,适合稠密图
Map[Size][Size];
//顶点之间有边Map[i][j] = 1 或者等于权值 i,j之间无边等于∞
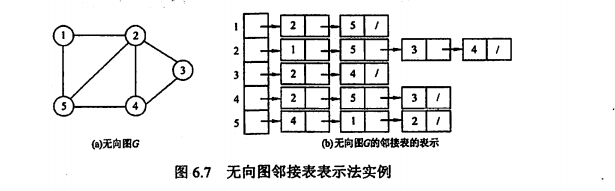
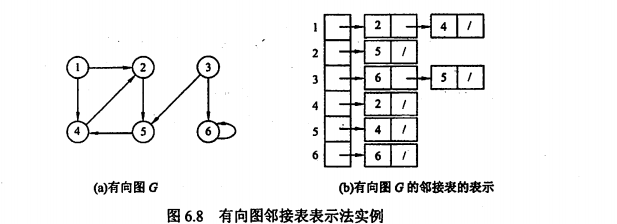
2.2 邻接表法
由顶点表和边表构成,顶点表数组代表所有的顶点,边表表示依附此顶点的边。
struct VerNode
{char ver;ArcNode *first;
};//顶点表struct ArcNode
{int adjvex;ArcNode *next;
};//边表具体图的存储实现移步例外一篇
2.3 十字链表法
只能存储有向图且空间开销太大
定义:
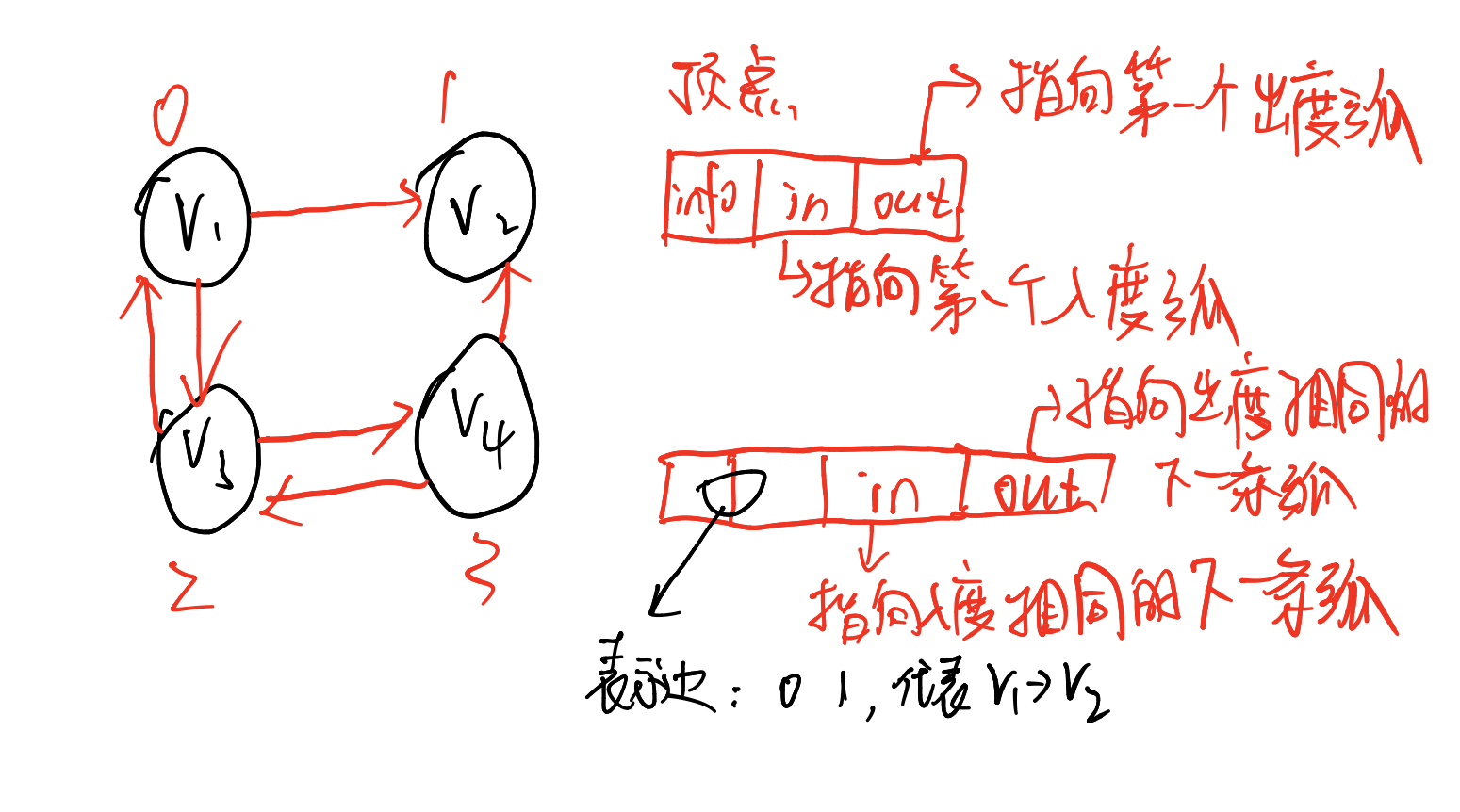
如何画出图的十字链表:
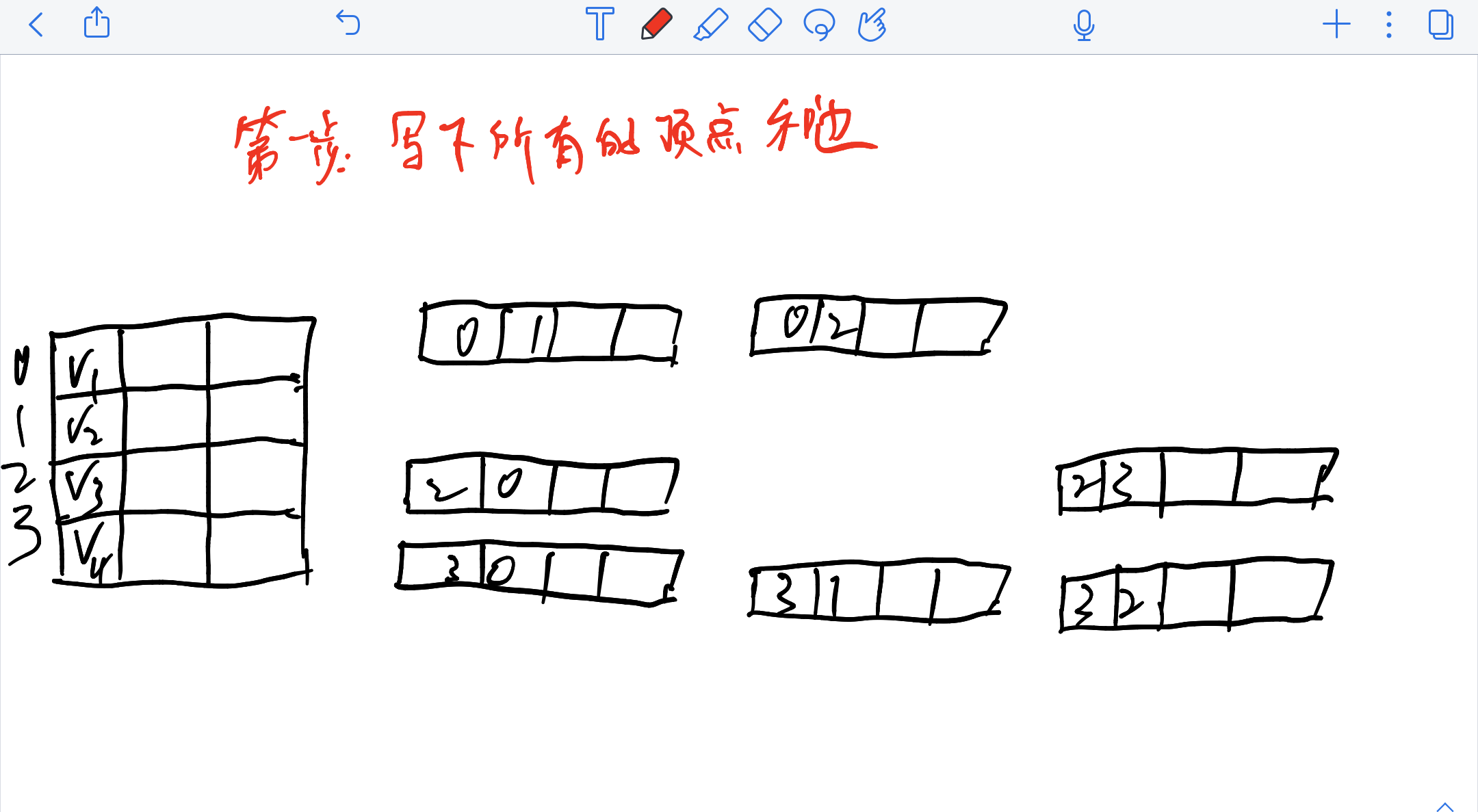
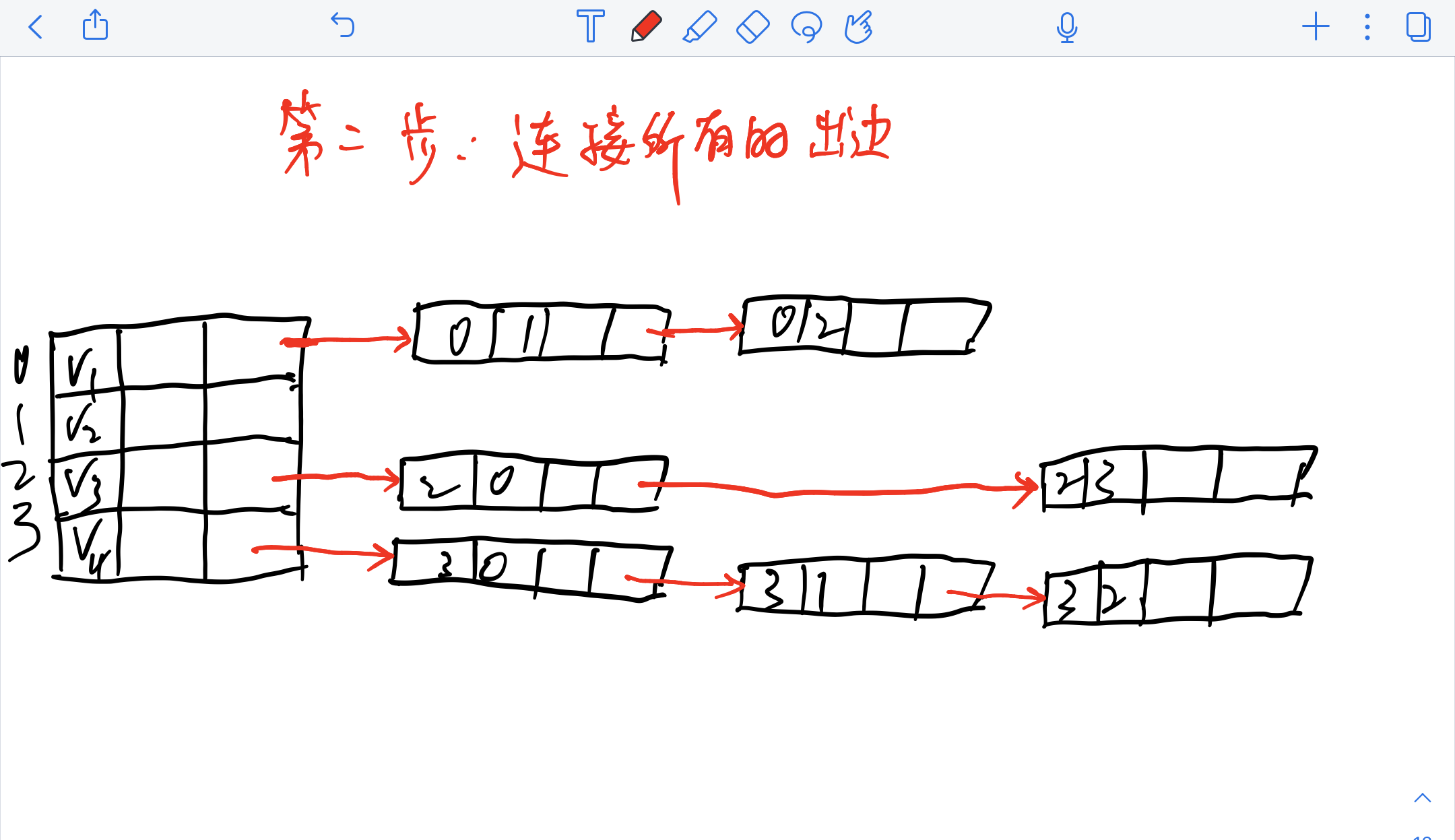
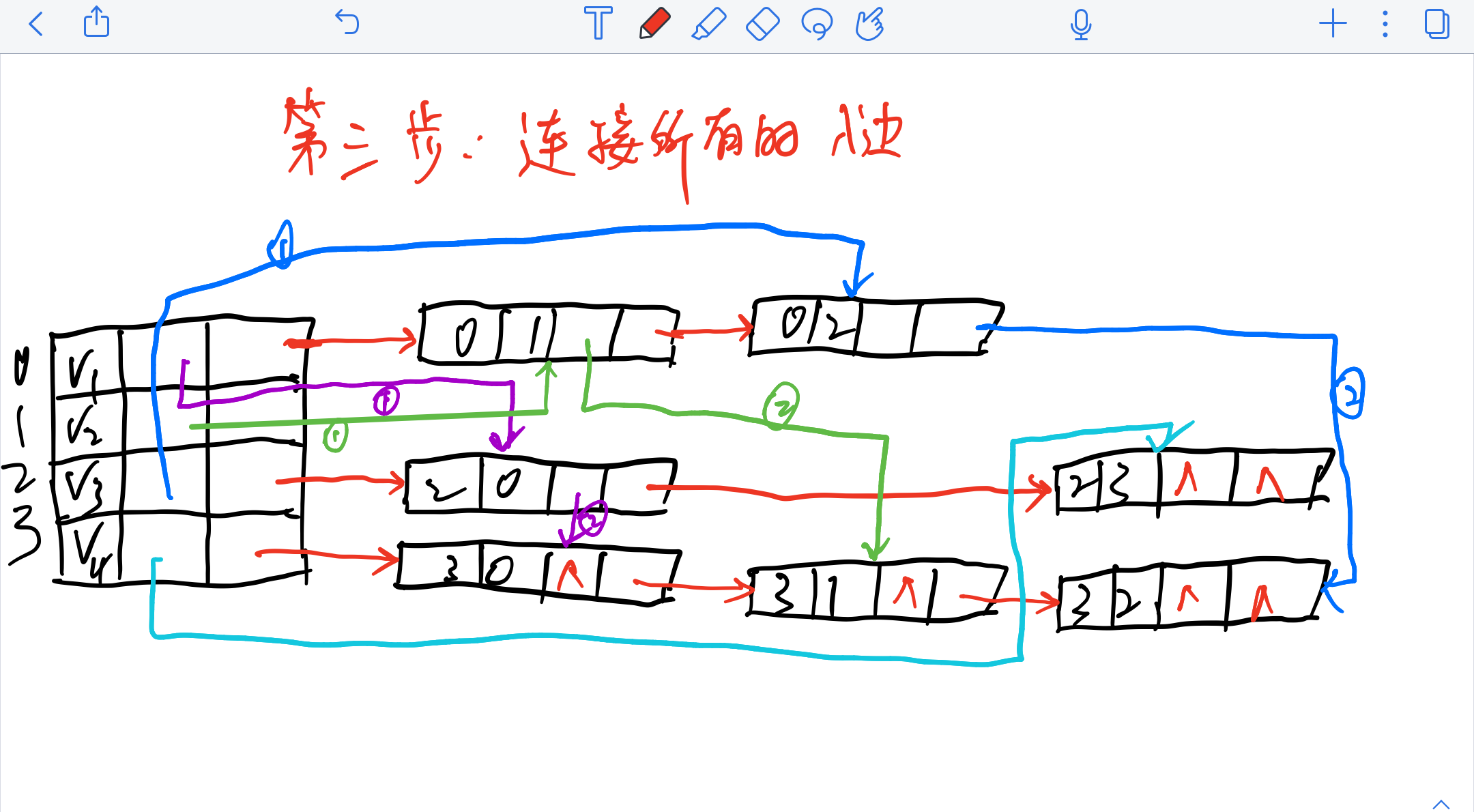
2.4 邻接多重表
无向图的另外一种存储方式
顶点表结构:

边结点结构如下所示:

iVex和jVex表示该边的两个顶点在顶点数组adjmultiList[num]中的位置;iLink和jLink分别表示指向依附于顶点iVex和jVex下一条边的指针
如何画出邻接多重表:
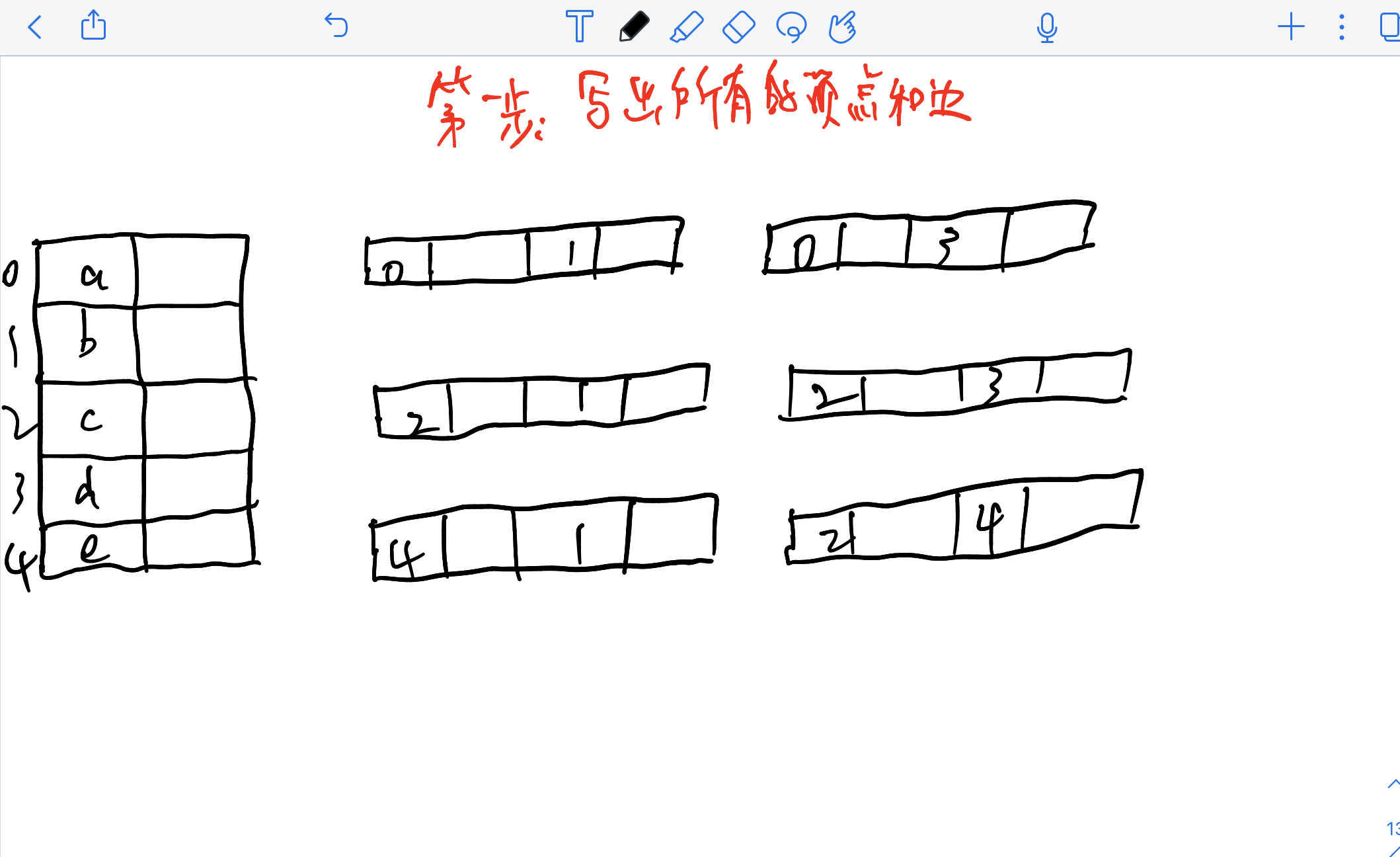
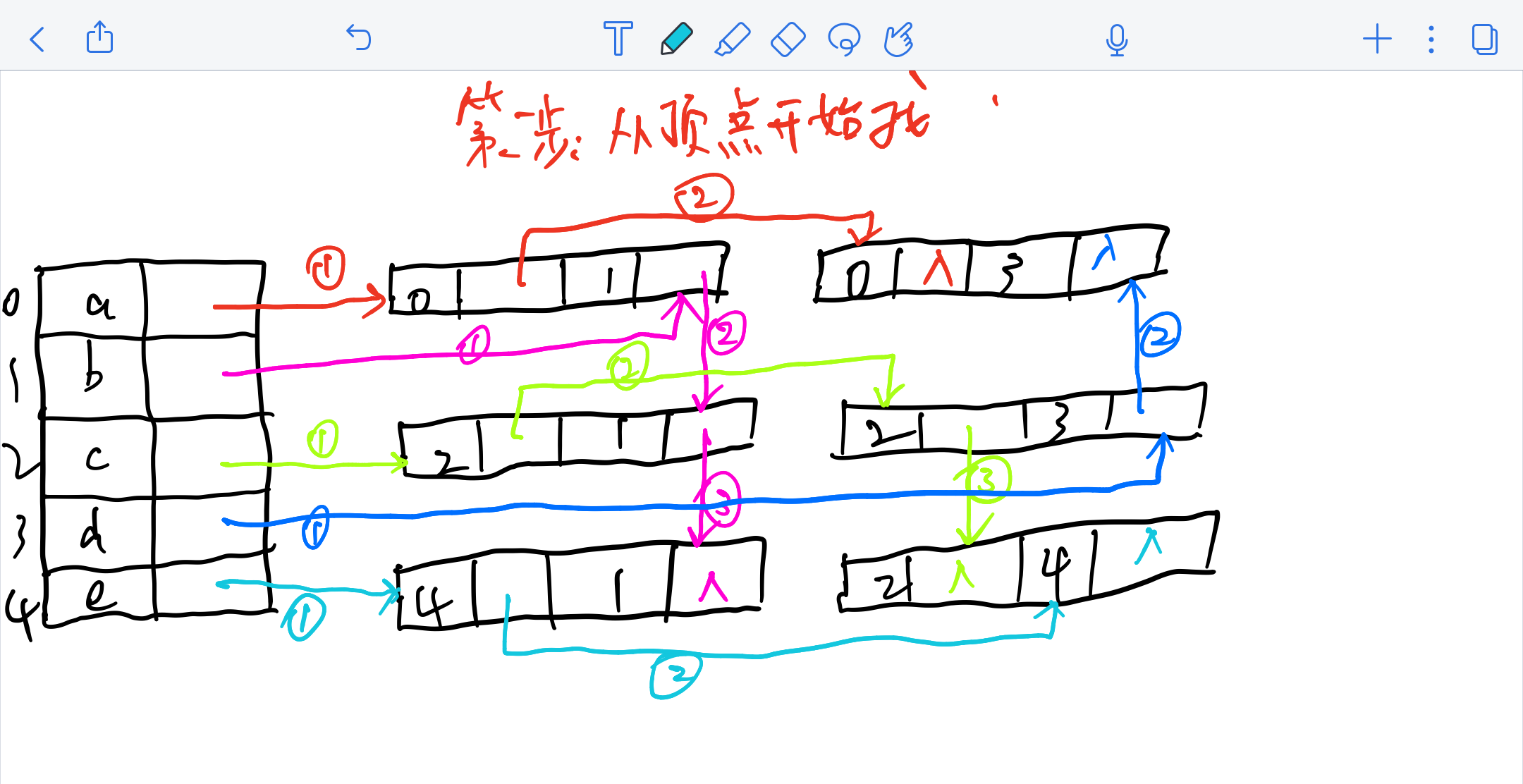
3 图的遍历
3.1 dfs(深度优先遍历)
类似于树的前序遍历,利用递归的思想遍历图的所有节点
void ALGraph::DFS(int v){int j;ArcNode *p;cout<<adjlist[v].ver<<" ";visited[v] = 1;p = adjlist[v].first;while(p){j = p->adjvex;if(visited[j] == 0)DFS(j);p = p->next;}}
3.2 bfs(广度优先遍历)
类似于树的层序遍历,同样用队列对每一个即将遍历的顶点进行入队出队操作,同时将他的邻接节点入队,直到队列为空。(可以用数组模拟队列的出队,入队操作)
为了在遍历过程中区分顶点是否被访问,设置一个访问标志数组visited[i],其初值为0,如果被访问,则置为0;
void ALGraph::BFSA(int v) // 数组模拟队列{int queue[Size];int rear,front,i,j,tem;ArcNode *p;memset(visited,0,sizeof(visited));rear = front = -1;queue[++ rear] = v;visited[v] = 1;p = adjlist[v].first;cout<<adjlist[v].ver<<" ";while(rear != front){v = queue[++ front];p = adjlist[v].first;while(p != NULL){j = p->adjvex;if(visited[j] == 0){cout<<adjlist[j].ver<<" ";visited[j] = 1;queue[++ rear] = j;}p = p->next;}}}
void ALGraph::BFSB(int v) //使用队列{queue<int> q;int j;ArcNode *p;memset(visited,0,sizeof(visited));q.push(v);visited[v] = 1;cout<<adjlist[v].ver<<" ";p = adjlist[v].first;while(!q.empty()){v = q.front(); q.pop();p = adjlist[v].first;while(p){j = p->adjvex;if(visited[j] == 0){cout<<adjlist[j].ver<<" ";q.push(j);}p = p->next;}}}void ALGraph::DFS(int v){int j;ArcNode *p;cout<<adjlist[v].ver<<" ";visited[v] = 1;p = adjlist[v].first;while(p){j = p->adjvex;if(visited[j] == 0)DFS(j);p = p->next;}}具体完整的代码在这篇文章
4 最小生成树
4.1 Prim
核心思想:把要生成的看做一个集合,用一个数组存储集合外的点到这个集合中点的最短距离,每次从集合中选择最小的距离,并把新的点加入到集合中,直到外部没有点
int min(shortEdge a[],int n)
{int minCost = 10000;int i,j;for(i = 0;i < n;i ++){if(a[i].lowcost != 0&&a[i].lowcost < minCost){minCost = a[i].lowcost;j = i;}}return j;
}int main()
{int verNum,arcNum;int i,j,k,root;cin>>verNum>>arcNum>>root; //root表示节点 1~verNum,输入root选取根节点init(verNum,arcNum);for(i = 0;i < verNum;i ++){sss[i].lowcost = arc[root - 1][i];sss[i].adjvex = root - 1;} //最短边集初始化sss[root - 1].lowcost = 0;for(i = 1;i < verNum;i ++){k = min(sss,verNum); //选取权值最小的边sss[k].lowcost = 0; //将顶点加入V中cout<<"("<<(sss[k].adjvex + 1)<<","<<(k + 1)<<")";for(j = 1;j < verNum;j ++){ //更新候补最短边集if(arc[k][j] < sss[j].lowcost){sss[j].lowcost = arc[k][j];sss[j].adjvex = k;}}}return 0;
}详细过程移步这篇
4.2 kruskal
kruskal最重要的就是一个最短边集,不同于prim每次找到到集合中最短边的点,Kruskal找的是最短边集中的边,把不重复的边加入树中
详细过程看这篇
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;const int Size = 100;
int parent[Size];struct Edge
{int from,to;int info;
};struct Graph
{int vertex[Size];Edge bian[Size];int verNum,arcNum;
};void Kruskal(Graph p);
int FindRoot(int parent[],int v);main()
{struct Graph p;int i,j,k;cin>>p.verNum>>p.arcNum;for(i = 0;i < p.verNum;i ++){p.vertex[i] = i;}for(i = 0;i < p.arcNum;i ++){cin>>p.bian[i].from>>p.bian[i].to>>p.bian[i].info;}Kruskal(p);return 0;}void Kruskal(Graph p)
{int num,i,j,vex1,vex2,ans;memset(parent,-1,sizeof(parent));for(i = 0;i < p.arcNum;i ++){ //根据边集的权值由小到大排序for(j = i;j < p.arcNum;j ++){if(p.bian[i].info > p.bian[j].info){Edge tem = p.bian[i];p.bian[i] = p.bian[j];p.bian[j] = tem;}}}for(num = 0,i = 0;i < p.arcNum;i ++){vex1 = FindRoot(parent,p.bian[i].from); //找到根节点vex2 = FindRoot(parent,p.bian[i].to);if(vex1 != vex2) //判断是否为同一连通分量{cout<<"("<<p.bian[i].from<<","<<p.bian[i].to<<")"<<" ";parent[vex2] = vex1; //将vex2的上一节点设置为 vex1num ++;if(num == (p.verNum - 1)) break;}}
}int FindRoot(int parent[],int v) //寻找根节点
{int t = v;while(parent[t] != -1){t = parent[t];}return t;
}/*
6 10
1 2 6
1 3 1
1 4 5
2 3 5
3 4 5
2 5 3
5 3 6
3 6 4
6 4 2
5 6 6(1,3)(3,6)(6,4)(3,2)(2,5)
*/5 最短路径
5.1 Dijkstra
核心:dist[j] = Min(dist[i]);for(k = 0;k < n;k ++)if(dist[j] > (dist[j] + arc[j][k] )dist[k] = dist[j] + arc[j][k];
模拟:
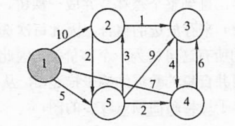

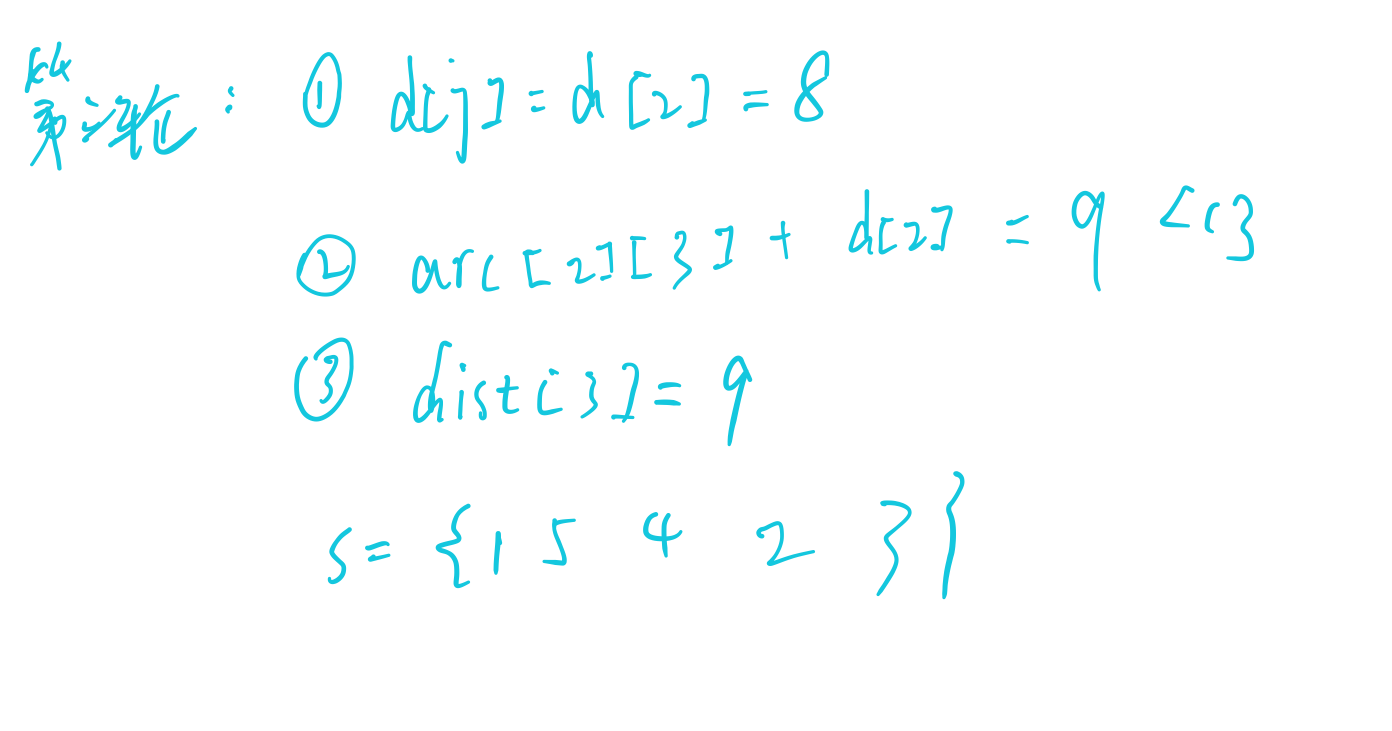
5.2 Floyd
动态规划,时间复杂度O(n³)
核心代码:
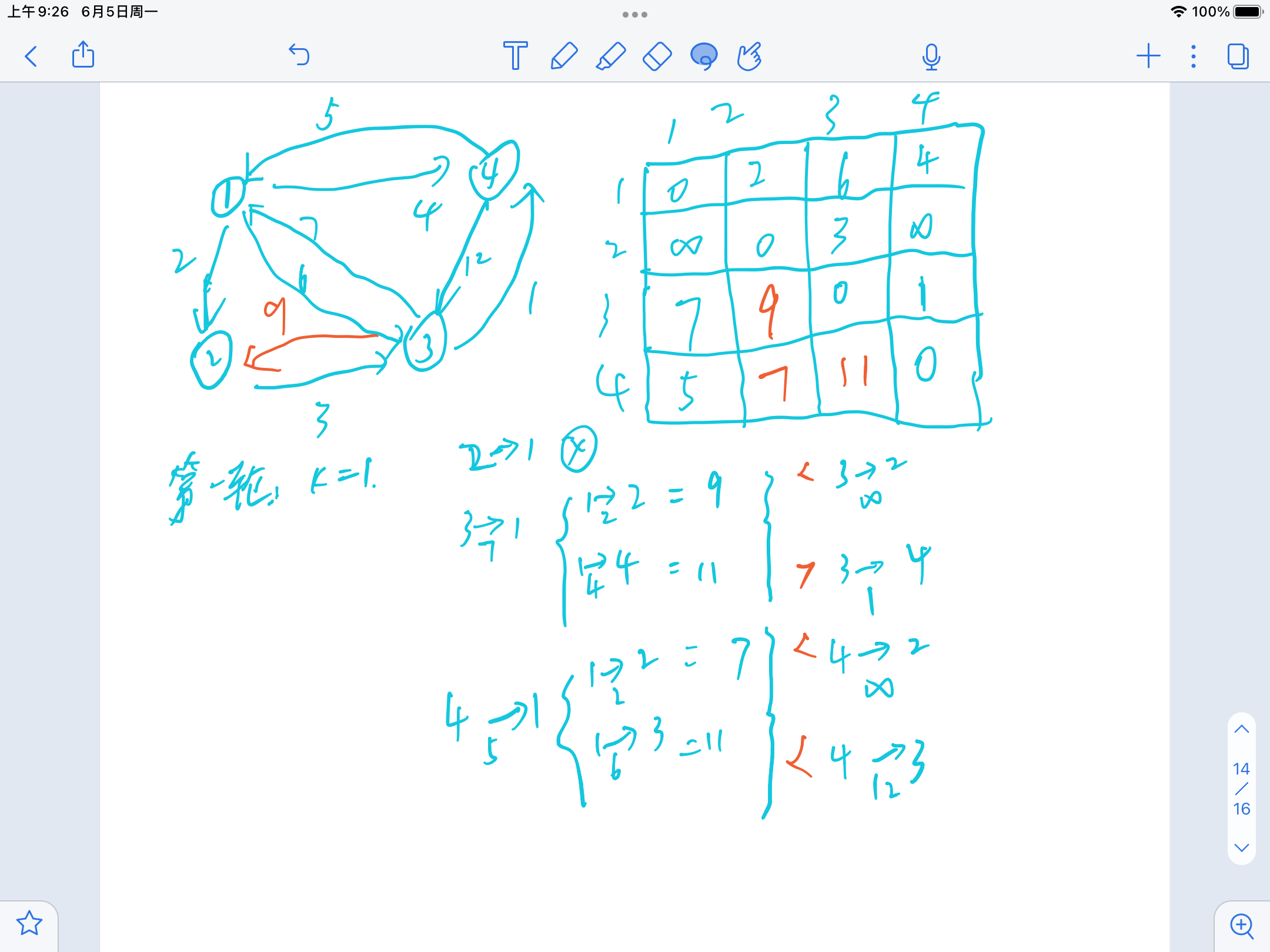
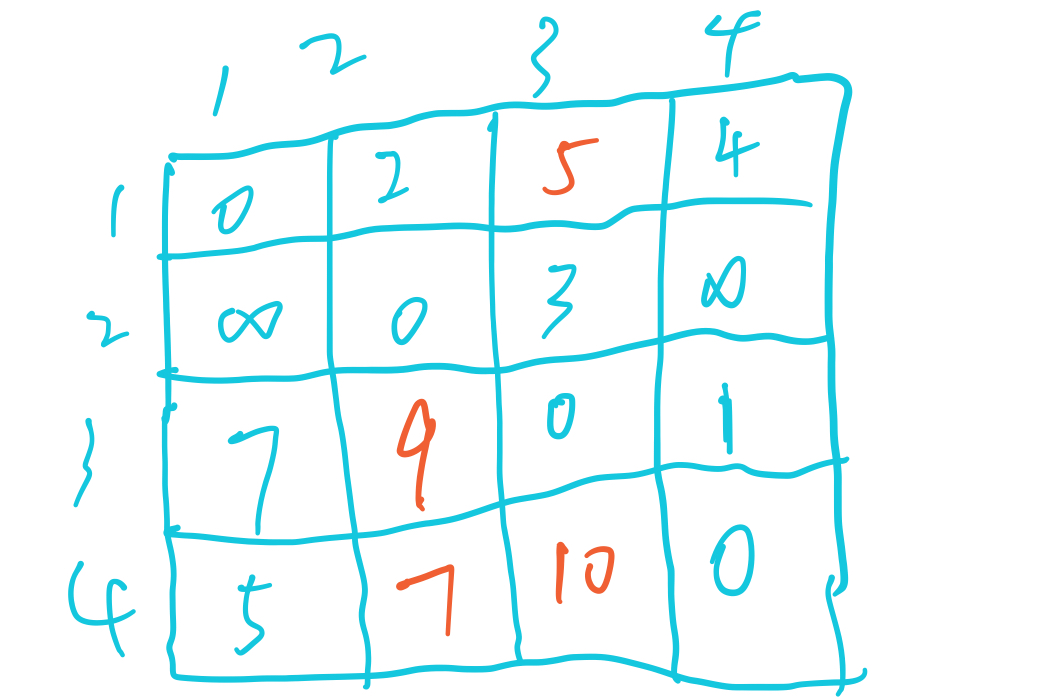
for(int k = 1;k <= n;k ++)for(int i = 1;i <= n;i ++)for(int j = 1;j <= n;j ++){if(arc[i][j] > arc[i][k] + arc[k][j])arc[i][j] = arc[i][j] > arc[i][k] + arc[k][j];}模拟:


6 AOV网和AOE网
6.1 AOV
定义:用DAG图(有向无环图)表示⼀个⼯程。顶点表示活动,有向边<Vi, Vj>表示活动Vi必须先于活动Vj进行。
拓扑排序:
1.选择一个入度为0的顶点输出。
2.删除该顶点和以它为起始的边。
3.重复1,2
逆拓扑排序:
1.选择一个出度为0的顶点输出。
2.删除该顶点和以它为终点的边。
3.重复1,2
6.2 AOE
定义:边上有权值的AOV网。
性质:
1.只有某顶点所代表的事发生后,从该顶点出发的各有向边代表的活动才能开始。
2.只有在进入某顶点的各有向边所代表的活动都已结束时,该顶点所代表的事才难发生。
关键路径: