1. 题目

1.1 题目描述

Given an array of integers nums and an integer target, return indices of the two 
numbers such that they add up to target. You may assume that each input would have 
exactly one solution, and you may not use the same element twice.
You can return the answer in any order.

Example 1:

Input: nums = [2,7,11,15], target = 9
Output: [0,1]
Explanation: Because nums[0] + nums[1] == 9, we return [0, 1].

Example 2:

Input: nums = [3,2,4], target = 6
Output: [1,2]

Example 3:

Input: nums = [3,3], target = 6
Output: [0,1]

Constraints:

2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
Only one valid answer exists.

2. 解答

2.1 baseline

一个比较直观的想法是，罗列出所有的可能方案，然后找到和等于target的方案，返回即可。这里面蕴含的数学概念是：组合，从n个元素中取出2个元素; 用数学公式表示为 $c_{n}^{2}$ 。
在用代码表示 $c_{n}^2$ 之前，可以先绘制一下示意图：

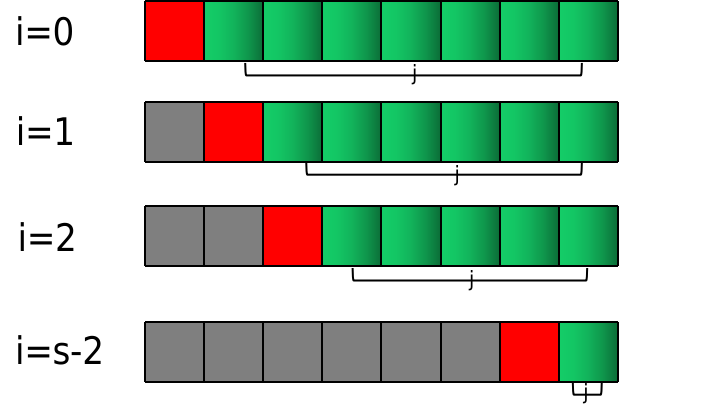
根据该示意图不难写出对应的代码。

class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {for(int i = 0; i < nums.size() - 1; ++i){for(int j = i + 1; j < nums.size(); ++j){if(target == nums[i] + nums[j]){return {i, j};}}}return {-1, -1};}
};

2.2 基于baseline的思考

baseline是一种“Brute Force”的思想，它的时间复杂度是 $o(n^2)$ ，这个时间复杂度极大概率不是最优的。
多层循环的常用优化点在于将循环解耦。例如将 $o(n^2)$ -----> $o (n) + o (n)$ 。外层循环表示的含义是数组中的每一个元素都有机会作为候选答案。因此这层循环很难去除。
来看内层循环：内层循环在做的事情是对于当前 $n u m s [i]$ , 通过遍历数组的方式，确认是否在其他元素中存在与之相加等于sum的元素；如果有找到答案。加粗的几个词语，是优化的关键：

“Brute Force”之所以效率低，是因为它在内循环中，试图以数组这一种数据结构，来解决查找问题。而数组的查找智能以遍历的方式进行，其查找的时间复杂度为n。

而哈希表(hashmap)这种数据结构，可以做到查找问题以 $o (1)$ 的时间复杂度进行。因此在进行真正的解决方案之前，先要根据数组构建对应的hashmap，以这种辅助数据的方式，将两层for循环进行解耦，从而时间复杂度降低为 $o (n) + o (n)$ 。

2.3 优化思路的实施

2.3.1 C++中的hashmap

hashmap(哈希表)是一个概念，不同编程语言对其有自己的实现。c++将其实现为std::unordered_map形式，(这边需要强调，不是std::map，std::map是对read-black tree的实现，其插入元素和访问元素的时间复杂度是 $l o g (n)$ )。
具体相关的代码有:

#include <unordered_map>  // 头文件
std::unordered_map<int, int> um;  // 定义一个unordered_map 对象
um.contains(k);  //判断k键值是否在um中，该时间复杂度是o(1) c++20才支持
um.find(k) != um.end();  //判断k键值是否在um中，该时间复杂度是o(1) c++11才支持
int index = um[k];  //获得k健值对应的value，该时间复杂度为o(1)

2.3.2 实施

class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {std::unordered_map<int, int> um;for(int i = 0; i < nums.size(); ++i){um[nums[i]] = i;}for(int i = 0; i < nums.size(); ++i){int another = target - nums[i];if(um.find(another) != um.end() && um[another] != i)return {i, um[another]};}return {-1, -1};}
};

这里要注意一下

um[another] != i

主要是对应题干中的you may not use the same element twice.

2.3.3 再思考

但该方案提交leetcode之后，耗时仍旧位于第二峰值区域。说明有继续优化的空间。目前的方案时间复杂度为 $o (N) + o (n)$ , 大写字母N表示是构建哈希表的部分，必须要遍历掉所有的元素；小写o(n)则是大概率仅仅会遍历部分元素，在中途就会找到答案中途退出。因此 $o (N)$ 是当前的瓶颈。这里面细分， $o (N)$ 是存在冗余信息的：
对于当前待查找对象nums[i], 我们只需知道在该元素之前是否有与之能够成功匹配的元素即可。因为若出现与nums[i]匹配的元素nums[ii]在i之后，则在处理元素nums[ii]的时候，nums[i]是作为ii之前，已经存在于hash表中的。这个时候nums[i]仍旧能够被翻出来。
这样做的好处在于将 $o (N) + o (n)$ 转变为 $o (n) + o (n)$ 。

2.3.4 最终实施

class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {std::unordered_map<int, int> um;for(int i = 0; i < nums.size(); ++i){int another = target - nums[i];if(um.find(another) != um.end())return {i, um[another]};um[nums[i]] = i; }return {-1, -1};}
};

此时的解决方案，就可以位于第一峰值处。
在这里插入图片描述

3. 总结

虽然"Brute Force"解法一般不是最优的，但快速的写出该解法作为baseline，是做进一步分析的前提。
分析耗时的瓶颈所在：两层for循环导致的 $o(n^2)$ 时间复杂度。往往可以借助于“辅助数据结构”，解耦到"o(N) + o(N)"的方案。而hashmap作为可以获得常量级插入和访问的数据结构，是非常优质的，需要熟悉其用法。
若想要进一步优化，“o(N) + o(n)” --> "o(n) + o(n)"是一种手段。因为此时的瓶颈在于o(N)。
最后在大的框架代码写完之后，要思考题干中的特殊限制代表的含义，例如you may not use the same element twice. 思考自己的代码是否已经体现了其含义。