纠错码可以帮助 QR 读码器检测 QR 二维码中的错误并予以校正。继对文本数据编码后，本篇将继续介绍生成纠错码的过程。

第一步：必要时将数据码拆分成块

在生成错误校正码之前，如果 QR 二维码大于版本 2，有必要将信息码拆分成小块。

错误校正表链接：
https://www.thonky.com/qr-code-tutorial/error-correction-table

举一个 5-Q QR 二维码的例子，由纠错表查得对应 62 个数据码字节（即 8 位二进制字符串的个数）。假设数据码字节如下：

(codeword #1) 01000011
(codeword #2) 01010101
(codeword #3) 01000110
(codeword #4) 10000110
(codeword #5) 01010111
(codeword #6) 00100110
(codeword #7) 01010101
(codeword #8) 11000010
(codeword #9) 01110111
(codeword #10) 00110010
(codeword #11) 00000110
(codeword #12) 00010010
(codeword #13) 00000110
(codeword #14) 01100111
(codeword #15) 00100110
(codeword #16) 11110110
(codeword #17) 11110110
(codeword #18) 01000010
(codeword #19) 00000111
(codeword #20) 01110110
(codeword #21) 10000110
(codeword #22) 11110010
(codeword #23) 00000111
(codeword #24) 00100110
(codeword #25) 01010110
(codeword #26) 00010110
(codeword #27) 11000110
(codeword #28) 11000111
(codeword #29) 10010010
(codeword #30) 00000110
(codeword #31) 10110110
(codeword #32) 11100110
(codeword #33) 11110111
(codeword #34) 01110111
(codeword #35) 00110010
(codeword #36) 00000111
(codeword #37) 01110110
(codeword #38) 10000110
(codeword #39) 01010111
(codeword #40) 00100110
(codeword #41) 01010010
(codeword #42) 00000110
(codeword #43) 10000110
(codeword #44) 10010111
(codeword #45) 00110010
(codeword #46) 00000111
(codeword #47) 01000110
(codeword #48) 11110111
(codeword #49) 01110110
(codeword #50) 01010110
(codeword #51) 11000010
(codeword #52) 00000110
(codeword #53) 10010111
(codeword #54) 00110010
(codeword #55) 11100000
(codeword #56) 11101100
(codeword #57) 00010001
(codeword #58) 11101100
(codeword #59) 00010001
(codeword #60) 11101100
(codeword #61) 00010001
(codeword #62) 11101100

错误校正表中提到了 “group 1” 和 “group 2”，也就是区块数。这也就意味着信息码要被拆分成两组，而且在每组内，信息码字也可能被继续拆成小块。信息码字是按顺序被拆分的（例如由码字 1 开始，然后码字 2 等）。

对于一个 5-Q 二维码，表中指出有两组码（Group），第一组中又被分成两块（Block），每块包含 15 个信息码字；第二组中也被分成两块，但每块包含 16 个码字。注意 15 + 15 + 16 + 16 = 62，正好是信息码字的总数。接下来我们将上面列出的 62 个码字拆分到对应的组和块，并以此解释该步骤过程：

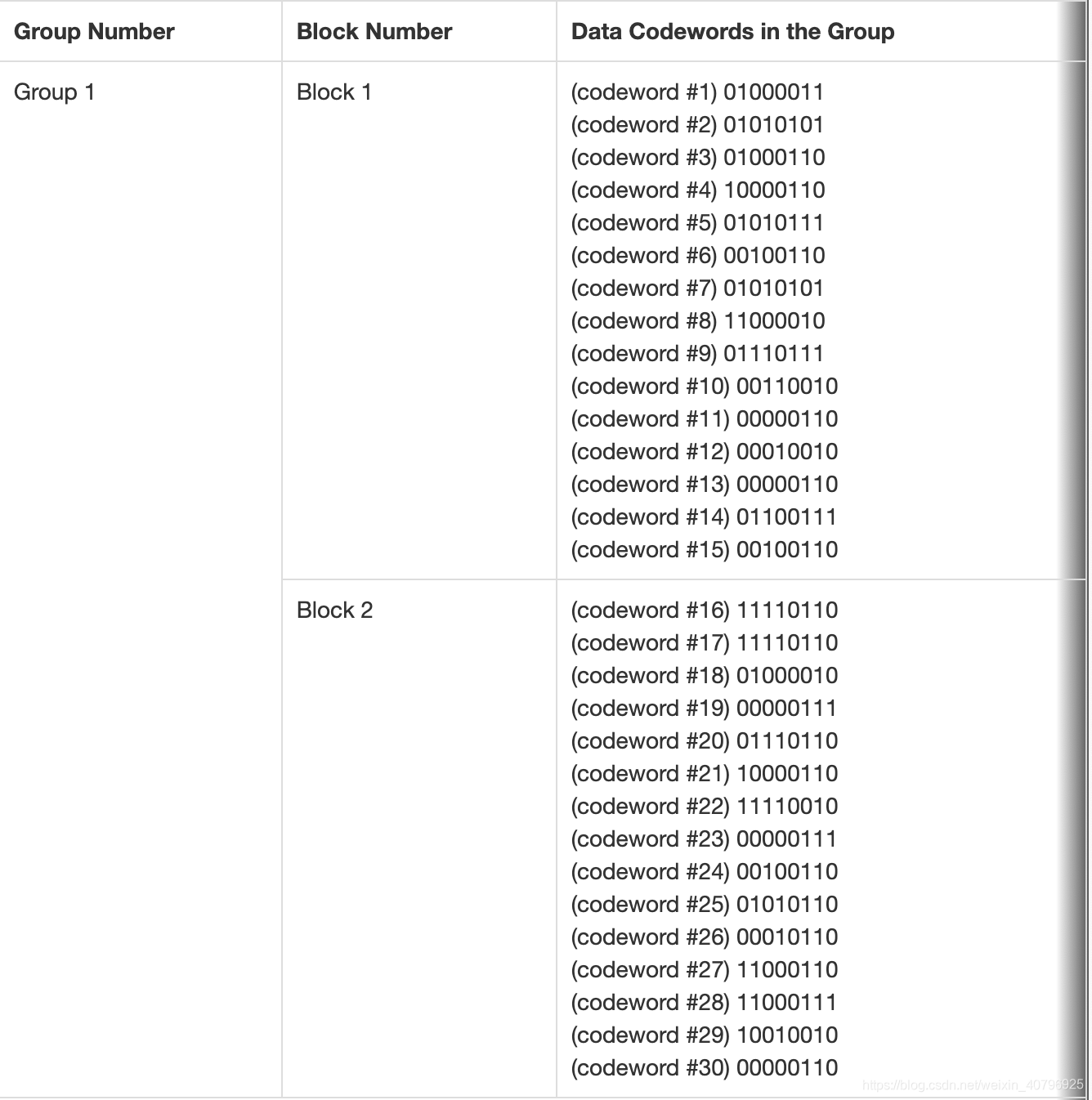
如上图，第一组每块包含 15 码字（8位2进制组成的字节），第二组每块包含 16 码字，并且拆分组块是按码字顺序排列出来的。换言之，拆分完后码字顺序与之前相同。

错误校正表还指出对于 5-Q 二维码，每块将有 18 个校错码字。承接上文例子，我们有四个块，因此也将会产生四套 18 个校错码字，共计 72 个校错码字。

同时纠错表中也可以看到，最小版 QR 二维码并不需要对信息码字进行拆分。例如 1-M 二维码所有的 16 个信息码字将被置于同一个独立块内，相应只需产生 10 个码字的纠错码。

在继续我们的 5-Q 例子之前，我们有必要先阐述下 Reed-Solomn 纠错方法中用到的下列步骤。

第二步：理解多项式相除

我们将采用 Reed-Solomon 纠错方法来生成纠错码。该方法中有个过程是执行多项式相除，即用一个多项式除以另一个多项式。本部分的前提是对手算除法有一定了解。

多项式除法较数字除法略复杂，这里我们举个例子说明。我们拿 3x^2 + x - 1 来除以 x + 1 ，图解过程如下：

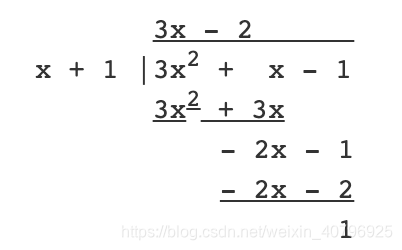
结果为 3x - 2 余数为 1。

总结下来，多项式除法的步骤如下：

1. 寻找合适的项与除数相乘，乘出来的结果应与被除数（在第一次相乘时）或上一步余数（第二次及之后相乘时）第一项相等
2. 被除数（第一次相乘时）或余数（第二次及之后相乘时）减去相乘结果
3. 重复步骤 1、2 直到除数无法继续和整数相乘。除式最底端的数字是余数

Reed-Solomon 纠错法中的多项式除法可能比这个要简单，因为不用去处理多项式中的指数。

第三步：理解有限域（The Galois Field）

实际上，域是一个可以在其上进行加法、减法、乘法和除法运算而结果不会超出域的集合。如有理数集合、实数集合、复数集合都是域，但整数集合不是（很明显，使用除法得到的分数或小数已超出整数集合）。

如果域F只包含有限个元素，则称其为有限域。有限域中元素的个数称为有限域的阶。尽管存在有无限个元素的无限域，但只有有限域在密码编码学中得到了广泛的应用。每个有限域的阶必为素数的幂，即有限域的阶可表示为pⁿ（p是素数、n是正整数），该有限域通常称为Galois域(Galois Fields)，记为GF(pⁿ)。

当n=1时，存在有限域GF（p），也称为素数域。在密码学中，最常用的域是阶为p的素数域GF（p）。
百度百科-有限域

Reed-Solomon 纠错法除了用到多项式除法，还用到了有限域，其本质上是一个数字集合，其域中的运算结果仍然在该数字集合内。

QR 二维码规范提到其使用以 2 为模的逐位算法和以 100011101 为模的逐字节算法。这意味着其采用 有限域 2^8，或者称之为 Galois Field 256，有时计作 GF(256)。

GF(256) 有限域中的数字范围是从 0 到 255。注意该范围与 8 位字节所代表的数字范围相同。

这也意味着 GF(256) 中的数学运算产生的数字结果都可以用 8 位字节来表示。

第四步：理解有限域算法

上文提到，GF(256) 包含了从 0 到 255 的数字，其中的运算本质上是循环的，也就是说如果运算结果超出 255， 将会采用取模运算产生一个仍在域中的数字。

在有限域中，负数和正数值是相同的，所有 -n = n。换言之在有限域算法中看的是绝对值。

这意味着有限域中加减法是同等操作。在正常进行加减后会进行取模运算。同时由于我们采用以 2 为模的逐位算法，这和 XOR 运算结果相同。例如：

1 + 1 = 2 % 2 = 0

对应

1 XOR 1 = 0

0 + 1 = 1 % 2 = 1

对应

0 XOR 1 = 1

出于 QR 编码目的，所有域中的两个数的加减法我们采用 XOR 运算。

第五步：以 100011101 为模逐字节运算生成 2 的次幂

所有 GF(256) 中的数字都可以被表示为 2 的次幂。相应地，所有 GF(256) 中的数字都可以被表示为 2^n，其中 0<=n<=255。然而之前提过， GF(256) 中的数字范围是 0 到 255，因此 2^8 值为 256 看上去是超出域范围。

2^0 = 1

2^1 = 2

2^2 = 4

2^3 = 8

2^4 = 16

2^5 = 32

2^6 = 64

2^7 = 128

QR 二维码说明中指出采用以 100011101 为模的运算（二进制 100011101 对应十进制中的 285）。这就意味着当一个数字大于等于 256，它将会于 285 进行 XOR 运算。

换言之：

2^8 = 256 XOR 285 = 100000000 XOR 100011101 = 29

2^9 = 2^8 * 2 = 29 * 2 = 58

2^10 = 58 * 2 = 116

2^11 = 116 * 2 = 232

2^12 = 232 * 2 = 464 XOR 285 = 205

通过此过程，所有 GF(256) 域中的数字均可被表示为 2^n, n的范围是 0 到 255。通过使用以 100011101 为模的逐字节算法保证所有值都在 0 到 255之内。

第六步：理解用 log 及反 log 的乘法运算

上文所述所有值都可以被表示为 2^n，那么为了简化运算可以取 log 和 反 log。两个数字 p 和 q 相乘可以表示为：

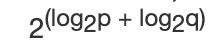
这也就意味着，因为所有 GF(256) 中的值也都可以被表示为 2 的次幂，那么域中所有乘法可以表示为 2 的指数相加。

例如 16 * 32 = 2^4 * 2^5 = 2^(4+5) = 2^9

上面计算过 2^9 = 58，因此 16*32 在 GF(256) 以 285 为模的逐字节算法下等于 58。

当指数相加时，如果指数大于 255，可以简化以 255 为模，例如：

2^170 * 2^164 = 2^(334) = 2^(334%255) = 2^79

因此，在 GF(256) 进行乘法是为了获得所有的 2 的次幂。所有值都被预先计算好，可以在 log 和 反 log 表中 查到。表中 alpha = 2，0 到 255 的数字都可以对应到 2 的 0 到 255 次幂，同时 2 的 0 到 255 次幂也都可以对应到 0到 255 的数字。

log和反log表
https://www.thonky.com/qr-code-tutorial/log-antilog-table

第七步：理解生成多项式

我们已经在生成纠错码的路上做了一番准备，但远还没有到实现的阶段，接下来我们还要理解生成多项式。

之前提到，纠错码使用了多项式除法。那么此过程需要两个多项式。第一个多项式是信息多项式，即使用数据码中的码字作为系数得到的多项式，例如如果数据码中的码字转化为整数是 25，218 和35，那么信息多项式将会是 25x^2 + 218x +35。实际上，标准二维码的真正的信息多项式要比这长得多，这里只是简单示例。

信息多项式将会被生成多项式相除。生成多项式是由 (x-alpha^{0)…(x-alpha}(n-1)) 相乘得到的，其中 n 为校错表中的纠错码中字节个数，alpha 值为 2。

我们可以通过程序生成所有需要的的生成多项式。在此处，我们利用上文中的 log 和 反 log 表乘法和 alpha 标记来讲解。

QR 二维码规范中列出了从 2 个开始到 68 个的生成多项式。尽管 QR 二维码总是需要超过 2 个纠错码/块，本篇只展示如何计算 2 个纠错码的过程，因为其它计算过程也是相似的。

2 个纠错码的生成多项式

首先使 (x-alpha^0) 和 (x-alpha^1) 相乘，由于 x 的系数是1 ，同时 alpha^0 = 1，所以可以被写成 alpha^0 * x^2 - (alpha^0 + alpha^1) *x^1 + alpha^1 * x^0

在 GF(256) 中，我们只关心绝对值，同时所有 0 到 255 的数字都可以通过 log 和 反 log 表找到对应的 2 的次幂值， alpha = 2，我们得到：

alpha^0 * x^2 + alpha^25 * x^1 + alpha^1 * x^0

这就是 2 个纠错码的生成多项式。

对于 3 个纠错码的生成多项式，在上面结果的基础上乘以 (x - alpha^3) 即可得到，以此类推，即可得到后续的所有生成多项式。

这也有个输入纠错码个数自动输出生成多项式的链接：

生成多项式小工具：
https://www.thonky.com/qr-code-tutorial/generator-polynomial-tool

第八步：生成纠错码

终于，我们走到了生成纠错码这一环节。这里我们采用之前 “HELLO WORLD” 在字符编码下生成的数据码。该数据码的字节将会被用作信息多项式的系数，本例子将采用纠错级别 M 和版本 1，最终生成 1-M 二维码。

信息多项式

之前拿到的 80 位数据码：

00100000 01011011 00001011 01111000 11010001 01110010 11011100 01001101 01000011 01000000

这里我们采用 1-M 二维码，需要 16 * 8 = 128 位的二进制串，我们还需要 48 位的补齐码，即 11101100 00010001 三组添加在后方得到 128 位：

00100000 01011011 00001011 01111000 11010001 01110010 11011100 01001101 01000011 01000000 11101100 00010001 11101100 00010001 11101100 00010001

将二进制转化为十进制数字得到 16 个数字：

32, 91, 11, 120, 209, 114, 220, 77, 67, 64, 236, 17, 236, 17, 236, 17

将其作为信息多项式系数，得到信息多项式：

32 * x^15 + 91 * x^14 + … + 17 * x^0

生成多项式

由于现在采用 1-M 二维码，通过纠错表我们可以查到需要生成 10 个纠错码，通过生成多项式的链接我们可以自动计算出，10 个纠错码的生成多项式如下：

除法步骤

接下来我们用信息多项式除以生成多项式，采用的是结合了有限域算法的多项式除法：

1. 寻找合适的项乘以生成多项式，使得乘法结果与被除数（第一次相乘）或余数（第二次及之后相乘）第一项相同
2. 对乘法结果和信息多项式（第一次乘法）或余数（第二次及之后）采用 XOR 运算
3. 重复执行步骤 1 和 2 共计 n 次，n 数据码的字节数

注意步骤不同于常规多项式除法，我们并没有采用乘法结果与被除数或余数相减，而是 XOR 运算（在 GF(256) 域中效果相同）。

更重要的是，经过相除之后，会生成余数。该余数多项式的系数即纠错码。

接下来我们一步步展示除法过程。

第九步：信息多项式除以生成多项式

首先我们准备好信息多项式，为了确保在相除过程中首项不会变得太小，我们用多项式整体乘以 x^ n,其中 n 为所需纠错码的个数。在本例中 n 为 10，乘以 x^10 得到：

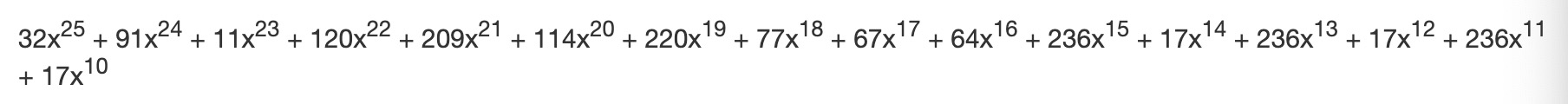
同理，我们也将生成多项式乘以 x^15 使得首项指数同级：

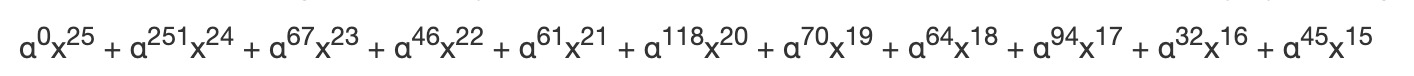
接下来要重复执行除法步骤，步骤次数即数据码的字节数、也就是信息多项式的项数，在本例中为 16 次。这将生成一个包含 10 项的余数多项式，这 10 项的系数即所求的10 个纠错码。

步骤 1a：第一次相除

首先对生成多项式乘以个 alpha^5 ，因为值等于 32，得到：

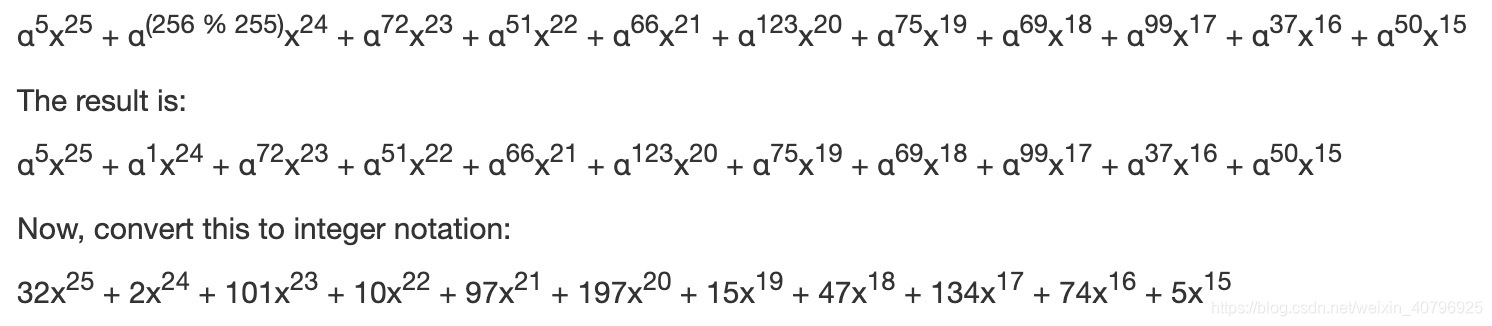
步骤 1b：将结果进行 XOR 运算

因为是第一次相乘，XOR 运算对象是信息多项式：

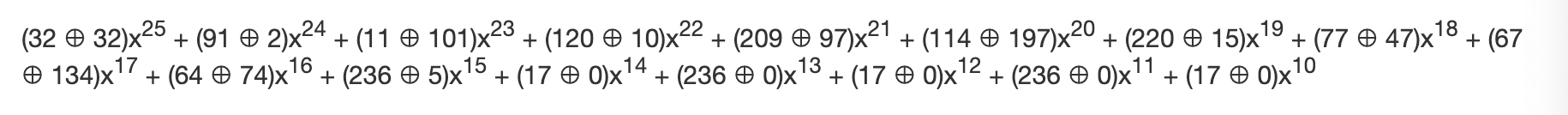
结果如下：

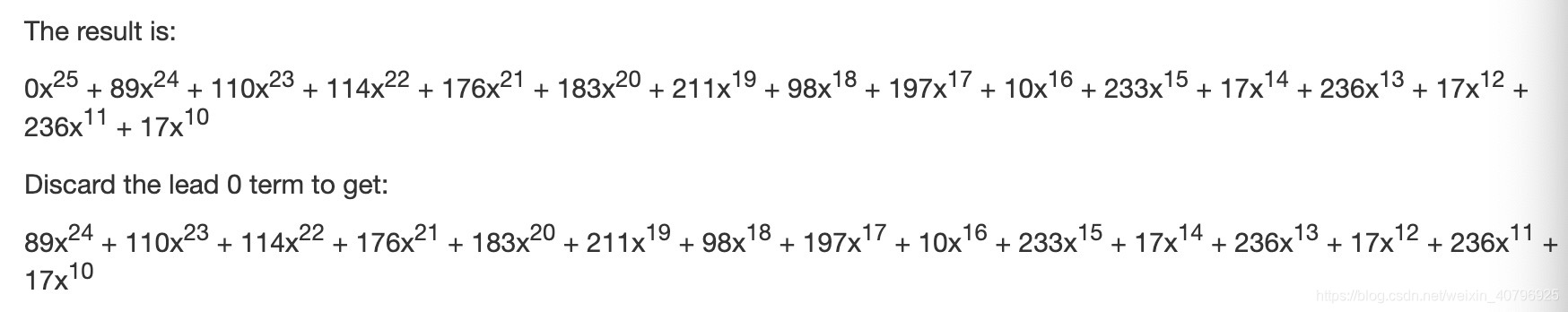
接下来我们会进行类似的步骤 2a,2b…16a,16b，最终生成余数多项式：

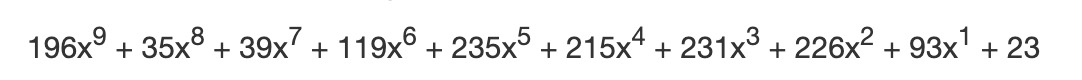
余数多项式的系数即我们需要的 10 个纠错码：

196 35 39 119 235 215 231 226 93 23

本文翻译自如下链接，篇幅原因省略了 2a,2b…16a,16b 等相似步骤
https://www.thonky.com/qr-code-tutorial/data-encoding