一、单一目标的雷达气象方程
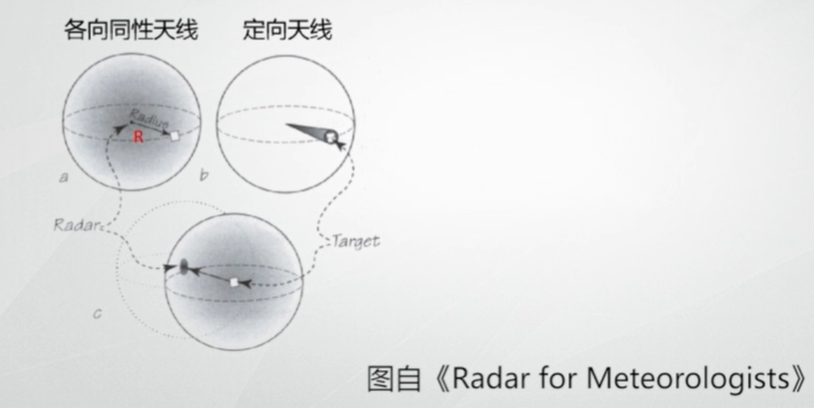
1. 各向同性的天线,假设雷达发射功率为
则在距离其为R处的能流密度为:
2. 实际的天线具有定向功能,可以将能量汇聚在一个狭窄的波束内
定向天线最大发射方向的能流密度与各向均匀辐射天线的能流密度之比,定义为天线增益G
3. 已知入射的能流密度基础上,结合我们前期学习的后向散射理论
目标散射回天线的后向散射能流密度为:
入射的能流密度 * 后向散射的面积 / 球面的面积平方
4. 天线的有效截面积
由粒子后向散射回天线的能流密度,不能全部被具有外口截面积的接收天线所接收,仅有很小的一块面积能被接收,称之为天线的有效截面积。
它与电磁波波长的平方,天线增益成正比
5. 雷达接收的总后向散射功率(回波功率)为
表示为:后向散射能流密度 天线的有效截面积
为接收的回波功率
为雷达发射功率
为天线增益
为雷达波长
为雷达后向散射截面
为雷达和目标物的距离
- 以上就是普遍的雷达方式,适用于任何单目标的物体的探测
- 雷达接收的回波功率与探测目标特性、雷达本身参数有关
二、云与降水雷达气象方程
- 假设天线辐射强度在雷达波束内均匀分布,粒子谱相同,散射波是非相干波。
- 雷达接收的回波功率的时间平均,等于波束照射体积内各个云降水粒子的回波功率总和。
1. 有效照射深度
有效照射深度
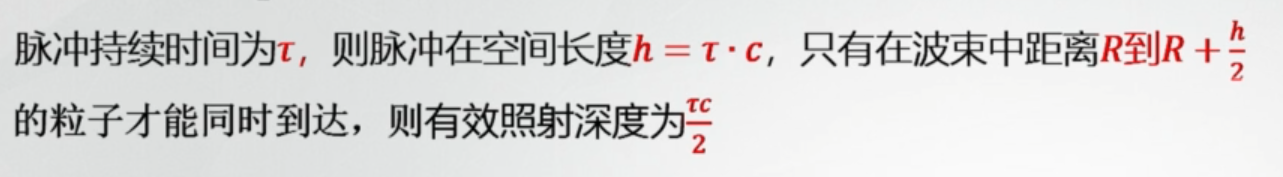
推导证明:
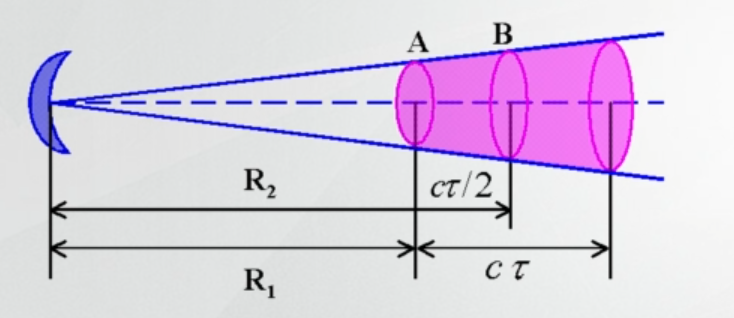
如图,假设波束中A点到天线的距离为R1,B点到天线的距离为R2,若取天线开始发射脉冲的时间为起始点,那么天线开始接收到A出粒子的散射能量时间t1,就等于两倍的R1除以c
雷达开始接受到B处粒子散射能量的时间为t2,等于两倍的R2除以c
最后接收到A粒子散射能量的时间t3,等于两倍的R1除以c在加上
假设在AB范围内粒子散射的能量能同时到达天线,那么天线开始接收到B处粒子散射能量的时间,正好是最后接收到A处粒子散射能量的时间,要求t2等于t3,通过该公式证明

2. 有效照射体积 V

V表示为椭圆的截面积乘以有效照射深度
常用的天气气雷达,基本采用抛物线天线,发射圆波束,即波束的水平和垂直宽度通常相等。
云与降水粒子的雷达气象方程:
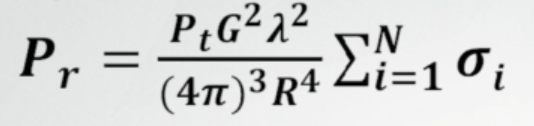
雷达有效照射体积中,所有云和降水粒子的后向散射截面之和。
这就是为什么假设在雷达采样体积内粒子谱处处相等

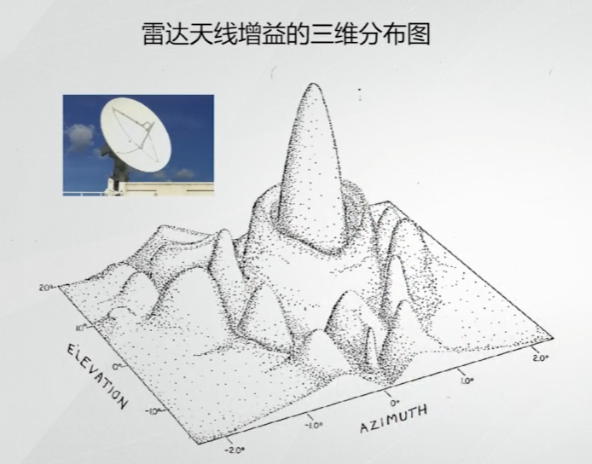
前面的推导中,我们假设在雷达波束内,天线的辐射强度处处相等,但实际的雷达天线增益的维分布图显示,在雷达波束内天线的辐射分布并不均匀。仅在波束指向方向,天线的增益才最大在其他方向均偏小。
因此,在前面推导的公式会高估接收功率。

假设在雷达的采祥体积里边,云和降水的粒子满足瑞利散射条件,那么雷达反射率可以解析地表示为球形粒子的后向散射。
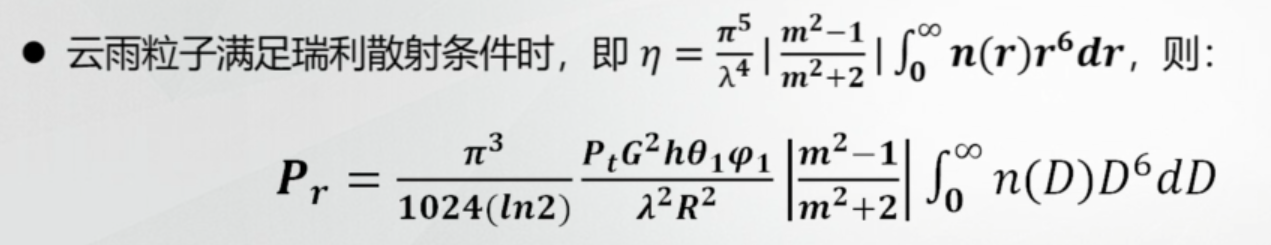
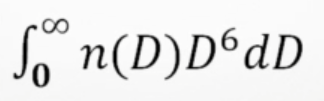
表示单位体积直径的六次方和,称为雷达反射率因子Z
简化:


该公式采用了两个假设条件:
- 满足瑞利散射的条件
- 粒子为球形
满足瑞利散射的条件
- 波长10cm时,雨滴0.01-0.5cm, 雪片0.01-3cm,冰雹0.5-2cm
- 波长5cm时,雨滴0.01-0.5cm, 雪片0.01-1cm,冰雹0.5-0.75cm
- 波长3cm时,雨滴0.01-0.5cm, 冰晶0.01 -0.5cm,霰0.1-0.5cm
- 波长0.8cm时,雨滴0.01-0.15cm, 冰晶0.01-0.15cm
波长10cm时:
雨滴尺寸很少超过六毫米,更大的雨滴下落中容易破碎。
小到中等尺度的冰雹也基本满足瑞利近似;
大冰雹则不满足。
波长3cm时:
对波长为3厘米的雷达,雨滴仍可用瑞利近似;
对霰和雹,只有小于0.5厘米直径才能用瑞利近似;
超过0.5厘米直径则不满足。
如不能满足瑞利散射近似
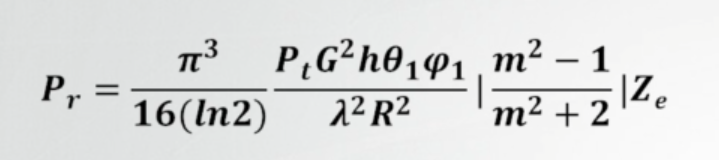
此时方程右边的Z,不再表示单位体积直径的六次方,而是用表示
其中为等效反射率因子,能够产生同样回波功率、与小球形粒子同样的
的数值.