传送门:
题意:
你现在有nnn个点,对于第iii个点,可以到达第i−1i-1i−1、2∗i2*i2∗i、2∗(i+1)2*(i+1)2∗(i+1)、⌊i2⌋\left \lfloor \frac{i}{2} \right \rfloor⌊2i⌋号点。现在问你从111号点开始的哈密顿路径。
分析:
一道非常有意思的题目。
我们需要发掘题目中隐藏的信息。
首先,假设该顶点不能到达第i−1i-1i−1个结点,对于任意一个点iii,因为它能够到达第2∗i2*i2∗i、2∗(i+1)2*(i+1)2∗(i+1)以及⌊i2⌋\left \lfloor \frac{i}{2} \right \rfloor⌊2i⌋,因此,由这些点所形成的结点必然能够形成一棵完全二叉树
显然一颗树是不能形成哈密顿回路的,显然这题的重中之重就是如何怎么选择去到第i−1i-1i−1个结点。
现在,如果加上到第i−1i-1i−1号结点的边,那么这张图将会变成这样:
而对于某一个结点iii,如果我们一直遍历2∗i2*i2∗i或2∗(i+1)2*(i+1)2∗(i+1)号结点,那么答案显然不会变优,因此我们需要在遍历图的过程中优先选择往i−1i-1i−1号结点访问,倘若i−1i-1i−1号结点被访问过了,则再访问第2∗i2*i2∗i号点。
这样进行dfs遍历之后,我们会发现我们形成了这样一棵dfs树:
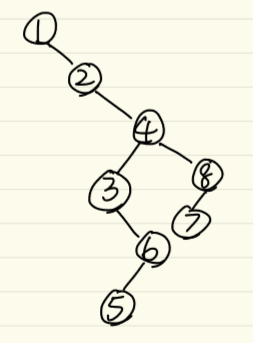
这棵dfs树所表示的即为遍历所有结点的顺序。此时我们只需要对这棵dfs树先遍历右儿子再遍历左儿子并把整张图输出即可。
需要注意的是,我们需要在遍历每一个点的时候判断一下当前点的第2∗(i+1)2*(i+1)2∗(i+1)号结点是否曾经在第一次dfs中访问,如果没有,则需要在此时输出。
代码:
#include <bits/stdc++.h>
#define maxn 100005
using namespace std;
typedef pair<int,int>pll;
pll q[maxn];
bool vis[maxn];
int n;
bool check(int x){return x>=1&&x<=n&&!vis[x];
}
void dfs(int x){vis[x]=true;if(check(x-1)){q[x].first=x-1;dfs(x-1);}if(check(x<<1)){q[x].second=x<<1;dfs(x<<1);}
}
void dfs2(int x){if(x==1) printf("1");else printf(" %d",x);if(check(x<<1|1)){vis[x<<1|1]=1;printf(" %d",x<<1|1);}if(q[x].second!=0){dfs2(q[x].second);}if(q[x].first!=0) dfs2(q[x].first);
}
int main()
{int t;scanf("%d",&t);while(t--){scanf("%d",&n);for(int i=1;i<=n;i++) vis[i]=false,q[i].first=q[i].second=0;dfs(1);dfs2(1);puts("");}return 0;
}