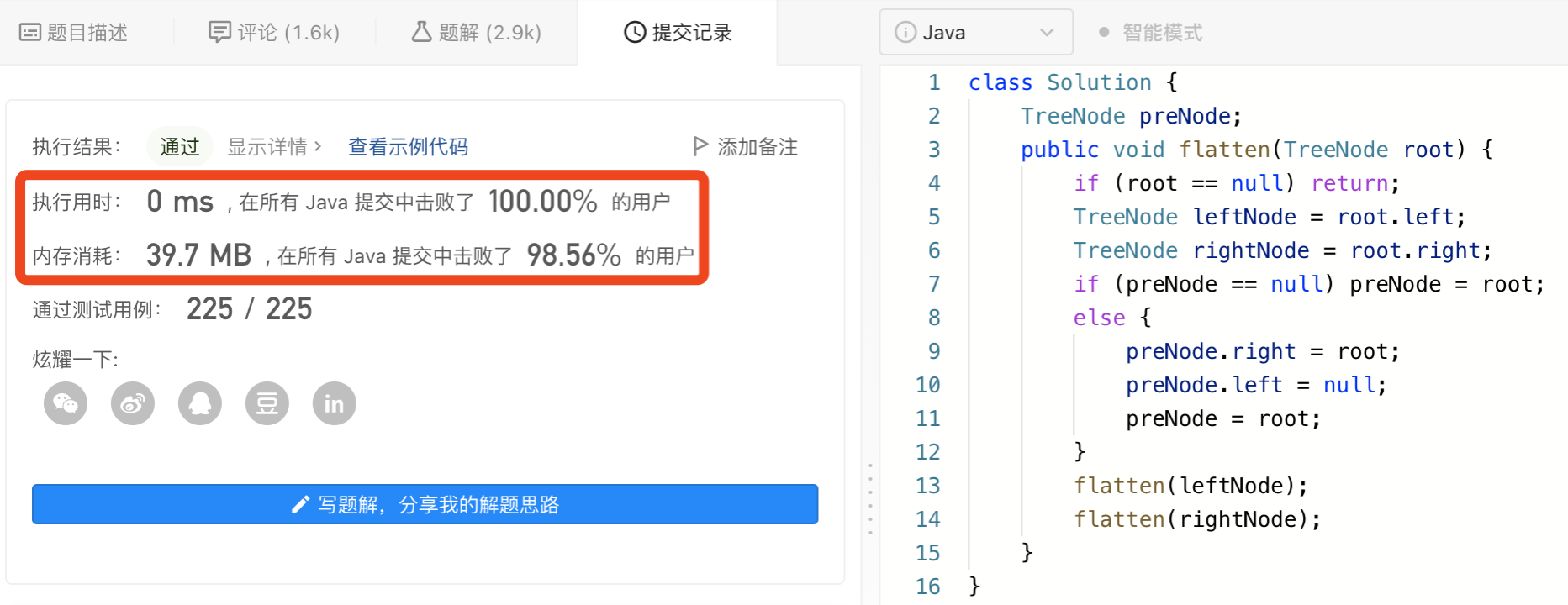
正题
题目链接:https://www.luogu.org/problemnew/show/P4130
题目大意
一个环形颜色珠子链,位置(注意不是上面的珠子)从最上顺时针下来位置依次标号 1 ∼ n 1\sim n 1∼n。
然后要求支持以下操作
- R k : R\ k: R k:将所有珠子顺时针旋转 k k k个。
- F : F: F:将所有珠子以 1 1 1向下翻转
- S i j : S\ i\ j: S i j:交换 i i i和 j j j上的珠子
- P i j k : P\ i\ j\ k: P i j k:将 i i i顺时针到 j j j的珠子都涂上颜色 k k k
- C : C: C:询问整个链有多少颜色段
- C S i j : CS\ i\ j: CS i j:询问 i i i顺时针到 j j j有多少颜色段。
(颜色段为连续的相同颜色)
解题思路
先不考虑前两个操作,我们可以用线段树进行操作。
储存 [ l , r , w , l c , r c , l a z y ] [l,r,w,lc,rc,lazy] [l,r,w,lc,rc,lazy]分别表示下标 l ∼ r l\sim r l∼r,有 w w w个颜色段,头颜色为 l c lc lc,尾颜色为 r c rc rc,懒惰标签 l a z y lazy lazy
然后我们可以利用 l c , r c lc,rc lc,rc进行合并。
之后我们就可以轻易的实现后4个操作。
那我们考虑前两个操作,我们会发现它并不会破坏连续性,也就是任何一个位置相邻的两个位置的数字编号也与其相邻。
那么我们就可以使用一个十分优秀的算法,我们用 t t t记录其旋转了几步,然后用 B B B记录是否翻转(因为翻转两次等于没有翻转)。之后就可以计算出给出的数字段旋转和翻转之前应该在哪个位置。
然后照样计算就好了。
c o d e code code
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=500100;
struct Tree_node{int l,r,w,lc,rc,lazy;
}ans;
int n,C,m,t,B;
struct Line_cut_tree{Tree_node t[N<<2];
// node merge(node tl,node tr)
// {
// node t;
// t.w=tl.w+tr.w+(tl.rc!=tr.lc);
// return t;
// }void megre(Tree_node &t,Tree_node tl,Tree_node tr){t.lc=tl.lc;t.rc=tr.rc;t.w=tl.w+tr.w-(tl.rc==tr.lc);}void build(int x,int l,int r){t[x].l=l;t[x].r=r;if(l==r){scanf("%d",&t[x].lc); t[x].rc=t[x].lc;t[x].w=1;return;}int mid=(l+r)/2;build(x*2,l,mid);build(x*2+1,mid+1,r);megre(t[x],t[x*2],t[x*2+1]);}void downdata(int x){if(!t[x].lazy) return;t[x*2].lazy=t[x*2+1].lazy=t[x].lazy;t[x*2].w=t[x*2+1].w=1;t[x*2].lc=t[x*2].rc=t[x*2+1].lc=t[x*2+1].rc=t[x].lazy;t[x].lazy=0;}void Ask(int x,int l,int r){if(t[x].l==l&&t[x].r==r){if(!ans.rc) ans.lc=t[x].lc;megre(ans,ans,t[x]);return;}downdata(x);if(r<=t[x*2].r) Ask(x*2,l,r);else if(l>t[x*2].r) Ask(x*2+1,l,r);else Ask(x*2,l,t[x*2].r),Ask(x*2+1,t[x*2+1].l,r);megre(t[x],t[x*2],t[x*2+1]);}void Change(int x,int l,int r,int z){if(t[x].l==l&&t[x].r==r){t[x].w=1;t[x].lazy=t[x].rc=t[x].lc=z;return;}downdata(x);if(r<=t[x*2].r) Change(x*2,l,r,z);else if(l>t[x*2].r) Change(x*2+1,l,r,z);else Change(x*2,l,t[x*2].r,z),Change(x*2+1,t[x*2+1].l,r,z);megre(t[x],t[x*2],t[x*2+1]);}
}Tree;
void Reset()
{ans.w=ans.rc=0;}
void doing(int &x,int &y)
{if(!B){if(x>=t+1) x=x-t;else x=n-t+x;if(y>=t+1) y=y-t;else y=n-t+y;}else{if(x<=t+1) x=t-x+2;else x=t+n-x+2;if(y<=t+1) y=t-y+2;else y=t+n-y+2;swap(x,y);}
}
int main()
{scanf("%d%d",&n,&C);Tree.build(1,1,n);scanf("%d",&m);for(int i=1;i<=m;i++){char op[3];scanf("%s",op);if(op[0]=='C'){if(op[1]=='S'){int x,y;scanf("%d%d",&x,&y);if(x==y)x++,x--;doing(x,y);if(y>=x) Reset(),Tree.Ask(1,x,y);else {Tree_node a1,a2;Reset();Tree.Ask(1,x,n);a1=ans;Reset();Tree.Ask(1,1,y);a2=ans;if(B){swap(a1.lc,a1.rc);swap(a2.lc,a2.rc);swap(a1,a2);}Tree.megre(ans,a1,a2);}printf("%d\n",ans.w);}elseprintf("%d\n",max(Tree.t[1].w-(Tree.t[1].lc==Tree.t[1].rc),1));}else if(op[0]=='R'){int k;scanf("%d",&k);t=(t+k)%n;}else if(op[0]=='F') B^=1,t=n-t;else if(op[0]=='S'){int x,y;scanf("%d%d",&x,&y);doing(x,y);Reset();Tree.Ask(1,x,x);int a1=ans.lc;Reset();Tree.Ask(1,y,y);int a2=ans.lc;Tree.Change(1,x,x,a2);Tree.Change(1,y,y,a1);}else if(op[0]=='P'){int x,y,z;scanf("%d%d%d",&x,&y,&z);doing(x,y);if(y>=x) Tree.Change(1,x,y,z);else Tree.Change(1,x,n,z),Tree.Change(1,1,y,z);}}
}