题目描述

给你两个长度分别 n 和 m 的整数数组 nums 和 multipliers ，其中 n >= m ，数组下标 从 1 开始 计数。

初始时，你的分数为 0 。你需要执行恰好 m 步操作。在第 i 步操作（从 1 开始 计数）中，需要：

选择数组 nums 开头处或者末尾处 的整数 x 。
你获得 multipliers[i] * x 分，并累加到你的分数中。
将 x 从数组 nums 中移除。
在执行 m 步操作后，返回 最大 分数。

示例1

输入：nums = [1,2,3], multipliers = [3,2,1]
输出：14
解释：一种最优解决方案如下：
- 选择末尾处的整数 3 ，[1,2,3] ，得 3 * 3 = 9 分，累加到分数中。
- 选择末尾处的整数 2 ，[1,2] ，得 2 * 2 = 4 分，累加到分数中。
- 选择末尾处的整数 1 ，[1] ，得 1 * 1 = 1 分，累加到分数中。
总分数为 9 + 4 + 1 = 14 。

示例2

输入：nums = [-5,-3,-3,-2,7,1], multipliers = [-10,-5,3,4,6]
输出：102
解释：一种最优解决方案如下：
- 选择开头处的整数 -5 ，[-5,-3,-3,-2,7,1] ，得 -5 * -10 = 50 分，累加到分数中。
- 选择开头处的整数 -3 ，[-3,-3,-2,7,1] ，得 -3 * -5 = 15 分，累加到分数中。
- 选择开头处的整数 -3 ，[-3,-2,7,1] ，得 -3 * 3 = -9 分，累加到分数中。
- 选择末尾处的整数 1 ，[-2,7,1] ，得 1 * 4 = 4 分，累加到分数中。
- 选择末尾处的整数 7 ，[-2,7] ，得 7 * 6 = 42 分，累加到分数中。
总分数为 50 + 15 - 9 + 4 + 42 = 102 。

n == nums.length
m == multipliers.length
1 <= m <= 103
m <= n <= 105
-1000 <= nums[i], multipliers[i] <= 1000

分析

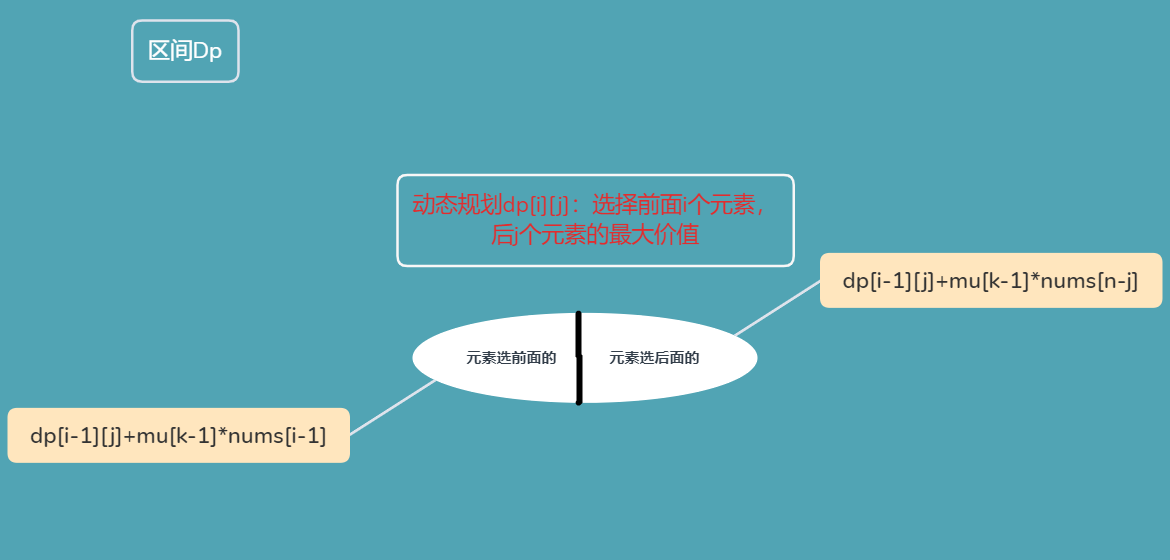
C++ 代码

class Solution {
public:typedef long long LL;int n,m,ans=INT_MIN;int maximumScore(vector<int>& nums, vector<int>& multipliers) {n=nums.size(),m=multipliers.size();vector<vector<int> >dp(m+2,vector<int>(m+2,INT_MIN));dp[0][0]=0;for(int k=1;k<=m;k++)   //枚举一共选取多少个元素{for(int i=0;i<=k;i++)   //i从第0个元素到第k个元素{int j=k-i;if(i) dp[i][j]=max(dp[i][j],dp[i-1][j]+multipliers[k-1]*nums[i-1]);if(j) dp[i][j]=max(dp[i][j],dp[i][j-1]+multipliers[k-1]*nums[n-j]);if(k==m) ans=max(ans,dp[i][j]); //k==m时为所有元素都取到了，此时取最大价值}}return ans;}
};