文章目录
- 7.2.1 顺序查找(线性查找)
- 顺序查找算法
- 设置监视哨的顺序查找
- 顺序查找算法分析
- 7.2.2 折半查找(二分或对分查找)
- 折半查找算法
- 折半查找性能分析 - 判定树
- 7.2.3 分块查找
- 分快查找算法
- 分块查找算法分析及比较
- 查找方法比较
7.2.1 顺序查找(线性查找)
应用范围:
- 顺序表或线性链表表示的静态查找表。
- 表内元素之间可以无序。
数据元素类型定义:
- 数据表可能有多个数据域的值,比如成绩表中有姓名、成绩、总分等。
- 所以用结构类型来表示要存储的数据元素的类型。
typedef struct
{Keytype key;//关键字域InfoType otherinfo;//其他域}ElemType;
顺序表的定义:
//顺序表结构类型定义
typedef struct
{ElemType* R;//存储空间基地址int length;//记录当前表用了多少个数据元素}SSTable;//Sequential Search Table
SSTable St;//定义顺序表 ST
顺序查找算法
顺序查找
- 在顺序表 ST 中查找值为 key 的数据元素。
- 例如:查找 13:找到,返回下标 5。查找 60:未找到,返回 NULL。
- 在此假设元素从 ST.R[1] 开始顺序向后存放,ST.R[0] 闲置不用,
- 查找时从表的最后开始比较,如下面的算法所示。
算法描述:
//在顺序表 ST 中顺序查找其关键字等于 key 的数据元素。
//若找到,则函数值为该元素在表中的位置(下标),反之返回0.int Search_Seq(SSTable St,KeyType key)
{for(i = St.length;i>=1;i--)//从表的最后开始往前找,i指向数组最后一个元素{if(key == ST.R[i].key){return i;//返回下标}}return 0;//循环完了还没找到说明里面没有要找的元素。
}
- 这种算法每进行一次循环都要进行两个比较,能否改进?
- 一次是看看查找的值是不是关键字的值,一次是判断 i 是否越界了。
- 这种算法用起来稍微麻烦了点,所以这时候就轮到哨兵出击了。
设置监视哨的顺序查找
改进:把待查找关键字 key 存入表头(哨兵、监视哨),从后往前逐个比较,可以免去查找过程中每一步都要检查是否检查完毕,加快速度。
- 假设现在要找的值时 60 ,将要找的值存进0号位置(监视哨)。
- 在找 60 的时候就不用考虑是否越界了。
- 一直从后往前找,如果在 0 号位置找到了 60,直接返回下标 0 。也就说明在 1-11号位置没有找到60。
算法描述
- 当 ST.length 比较大时,此改进能够使进行一次查找所需要的平均时间几乎减少一半。
//在顺序表 ST 中顺序查找其关键字等于 key 的数据元素。
//若找到,则函数值为该元素在表中的下标位置,反之返回0int Search_Seq(SSTable St,KeyType key)
{ST.R[0].key = key;//哨兵,将关键字的值放到下标为0的位置for(i = St.length;ST.R[i] != key;i--); //别忘了 for 后面的分号,忘了就完犊子了return i;
}
顺序查找算法分析
【设置监视哨的顺序查找】:时间效率分析
比较次数与 key 的位置有关:
- 查找第 i 个元素,需要边角 n- i + 1 次。
- 查找失败时,需要比较 n + 1 次。
顺序查找的性能分析
- 时间复杂度:O(n)
- 查找成功时的平均查找长度,设表中各记录查找概率相等。

- 查找成功时的平均查找长度,设表中各记录查找概率相等。
- 空间复杂度:O(1) 需要一个额外的辅助空间(哨兵)。
讨论:
- 记录的查找概率不相等时如何提高查找效率?
- 查找表存储记录原则 —— 按查找概率高低存储:
- 查找概率越高,比较次数越少,放在比较靠后的位置。
- 查找概率越低,比较次数越多,放在比较靠前的位置。
- 查找表存储记录原则 —— 按查找概率高低存储:
- 记录的查找概率事先不知道时该如何提高查找效率?
- 方法 —— 按查找概率动态调整记录顺序:
- 在每个记录中设置一个访问频度域;
- 始终保持记录按非递增有序的次序排列;
- 每次查找后均将刚查到的记录直接移动到表头。
- 方法 —— 按查找概率动态调整记录顺序:
顺序查找的特点
- 优点:算法简单,逻辑次序无要求,且不同存储结构均适用(顺序/链式存储均可)。
- 缺点:平均查找长度 ASL 太长,时间效率很低。
7.2.2 折半查找(二分或对分查找)
- 二分查找:每次将待查记录所在区间缩小一半。只对已经排序的数据有效。
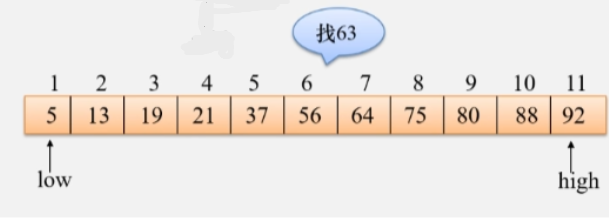
查找过程:
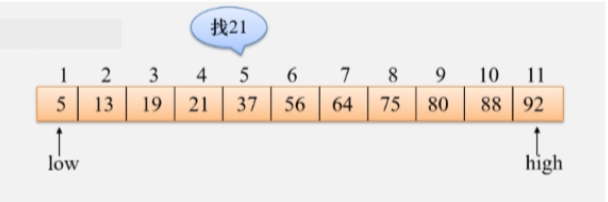
当前数组内的数据元素是按照升序排序的。
- 设置一个查找区间初始值,low 指向第一个元素,high 指向最后一个元素。
- 当 low <= high 时,循环执行以下操作:
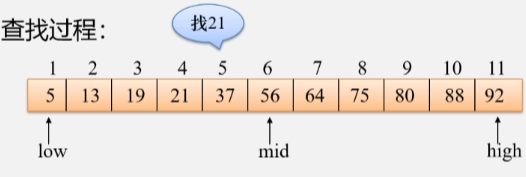
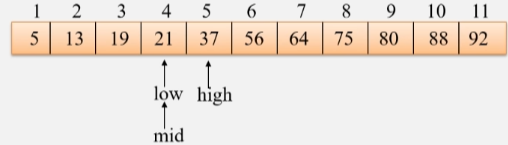
- 设一个 mid 为 low 和 high 的中间值:mid = (low + high) / 2,当前这个数组的 mid 是 下标 6的元素56。
- 直接将要找的这个关键字的值 21 和 和中间位置的这个值比较一下,发现 21 < 56,说明这个值一定在 mid 的左边。要将查找范围更新到 mid 左边。
- 则将新的 high 更新为:key < mid 则:high = mid - 1,因为中间位置也比较过来,不是这家伙。
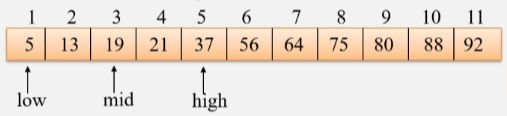
- 继续拿 mid 的值和 21 比较,发现 19 < 21,说明待查找的值在 mid 的右边,将 low 更新,key > mid 则: low = mid +1。
- 然后再去找中间位置,low是4 high 是5,min的值就是4。
- 拿 key 的值 21 和 mid 的值比较,发现 mid = key 则:return mid。
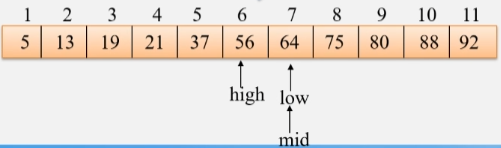
如果要找的值不在数组中:
- 查找到最后 low 会大于 high 上下限交换了,此时说明数组中没有俺们要找的数。
- high < low,结束。
折半查找算法
非递归算法 :
- 设表长为 n ,low、high 和 mid 分别指向待查元素所在区间的上限、下限和中点,令 key 为给定的要查找的值:
- 初始时,令 low = 1,high = n,mid = (low + high) /2
- 让 key 与 mid 指向的记录比较:
- 若 key == R[mid].key,则查找成功。
- 若 key < R[mid].key,则 high = mid + 1。
- 若 key > R[mid].key,则 low = mid + 1。
int serch_Bin(SSTable ST,KeyType key)
{low = 1;high = ST.length;//置查找区间初始值while(low <= high){mid = (low + high) / 2;if(ST.R[mid].key == key){return mid;//找到待查找元素}else if(key < St.R[mid].key){high = mid -1;//将查找区间缩小到 mid 左边}else{low = mid + 1;//将查找区间缩到 mid 右边}}return 0;
}
折半查找性能分析 - 判定树
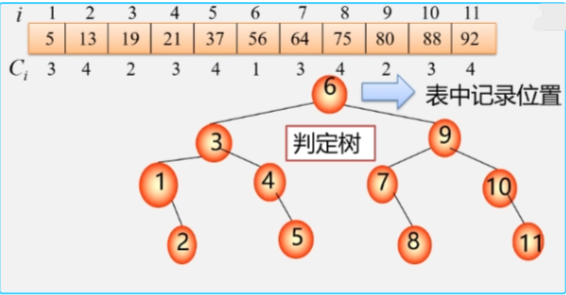
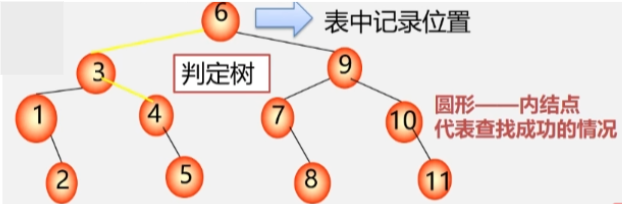
折半查找过程可以用二叉树来描述:
- 树中每一个结点对应表中一个记录,但结点值不是记录的关键字,而是记录在表中的位置序号。
- 把当前查找区间的中间位置作为根,左子表和右子表分别作为根的左子树和右子树,由此得到的二叉树称为折半查找的判定树。
- 结点所在层数表示该位置的元素需要比较多少次。
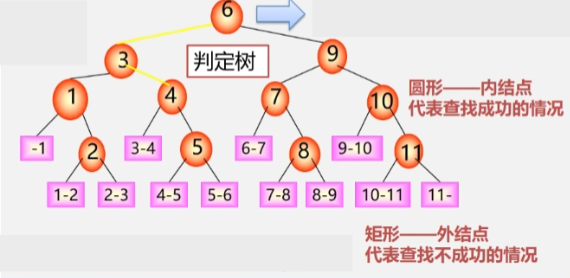
查找成功
- 比较次数 = 路径上的结点数。
- 比较次数 = 结点所在的层数。
查找不成功
- 比较次数 = 路径上的内部结点数。
- 比较次数 <= log₂n + 1。
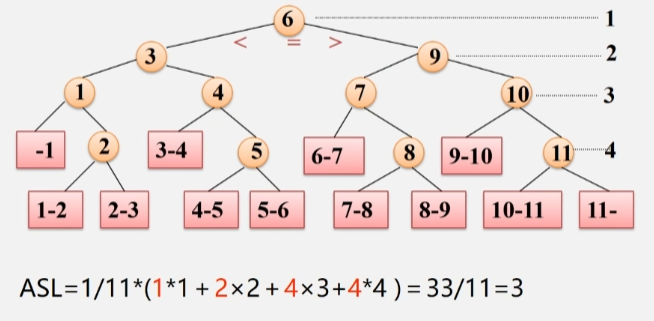
- 假设每个元素的查找概率相等,求查找成功时的平均查找长度。
- 所有元素的比较次数相加然后除与结点数。
平均查找长度 ASL(成功时):
- 设表长 n = 2h -1,则 h = log₂(n+1)(此时,判定树为深度 = h 的满二叉树),且表中每个记录的查找概率相等:Pi = 1/n。
折半查找特点:
- 缺点:效率比顺序查找搞。
- 缺点:只适用于有序表,且限于顺序存储结构(对线性链表无效)。
7.2.3 分块查找
分块查找:既能使查找效率比较高,又能方便的进行插入和删除。
分快查找算法
- 一般的字典(图1)俺们是用二分查找的方式来找的,随便翻开一页看到当前单词页的首字母,就知道是该往前还是往后翻了。
- 而不一般的字典(图2),将所有的单词按照首字母顺序划分成若干块,将这本书分成 26 块区域。
- 假设要找下面这个单词,直接翻开首字母为 m 的那一块区域,然后在这块区域进行 顺序查找 或者 二分查找。
- 这种查找方式就称作分块查找,也称索引顺序查找。
分块查找条件:
- 将表所有元素分成若干块,每一块的内容可以是有序的,也可以是无序的,如果是无序则称作分块有序。
- 分块有序:块间有序,块内无序。
- 块之间是有序的,单词是按 A ~ Z这样一个区域块排的,块内可以是无序的。都是字母 m 开头的单词可以随便放(当然字典不能真的随便放)。
- 定义:若第 i 块在第 j 块之前(i < j),则第 j 块中所有记录的关键字均大于第 i 块中的最大关键字。
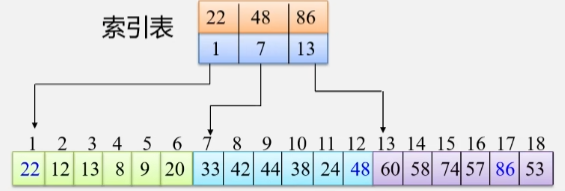
- 如:假设现有一个被分成 3 块的数据表,第一块中的最大值 22 肯定小于第 2、3 块中所有的值。
- 分块有序:块间有序,块内无序。
- 建立索引表(每个结点含有最大关键字域或指向本块第一个结点的指针,且按关键字有序)。
- 人话:记录每一块区域的最大值,以及每一块是从哪里开始的。
分快查找过程
- 先确定待查找记录(值)在哪块区域(用顺序或折半查找)。
- 再在块内查找(用顺序查找)。
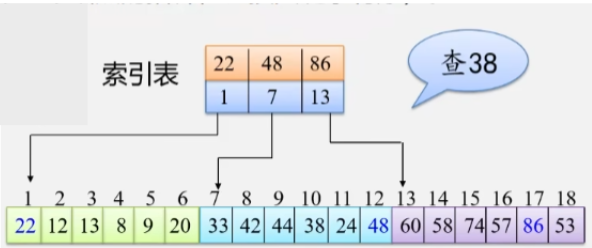
举个例子
- 先在索引表中找,第一块区域最大值是 22,那肯定不在第一块,38 < 48,所以在第二块区域找。
- 块内元素是无序的,所以就在第二块中进行顺序查找。
分块查找算法分析及比较
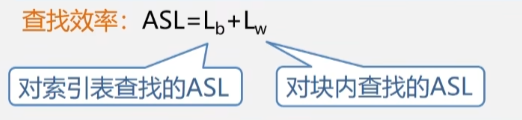
分块查找的平均查找次数为:在块之间比较的次数 + 块内查找的次数。
查找效率
- 其中:Lb 为查找索引表确定所在块的平均查找长度,Lw 为在块中查找元素的平均查找长度。
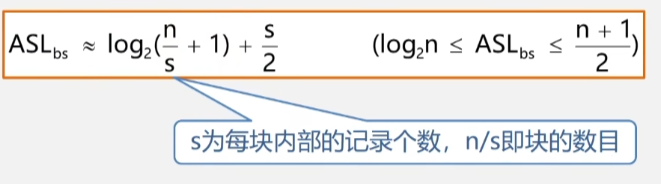
- 假设总共有 n 个元素,再假设每一块中有 s 个元素,所以索引表就可以分成 n / s 块。
- 在索引表中的平均查找长度就为:log₂(n / s +1)。
- 在块内进行查找:因为块内是无序的,无序就用顺序查找法,顺序查找的凭据查找长度就是 s / 2。
例如:
当 n = 9,s = 3 时
- 分块法的 ASLbs = 3.5。
- 折半法的 ASL ≈ log₂n = 3.1。但是折半法需要预先排序,所以任然需要时间。
- 顺序法的 ASL = (1+n)/2 = 5。
分块查找特点
- 优点:插入和删除比较容易,无序进行大量移动。
- 缺点:要增加一个索引表的存储空间并对初始索引表进行排序运算。
- 适用情况:如果线性表既要快速查找又经常动态变化,则可以采用分块查找。










![[Python]调用pytdx的代码示例](https://img-blog.csdnimg.cn/img_convert/bba4e2d5ac95754514e76cc0e9a8f5ba.png)