由数据范围反推算法复杂度以及算法内容 - AcWing

常用代码模板4——数学知识 - AcWing

基本思想：

     求一个数的n次时，我们的时间复杂度为O(n),当n特别大时，效率会很低可能超时，此时我们就需要运用到快速幂，将我们的时间复杂度降低到O(log n)。快速幂的核心思想是，我们预处理一些数据，然后将a^k用我们预处理的数据组合出来，即将a^k拆成若干个预处理的值，我们将k转化为二进制表示，就可以得到我们所需要的数据。

       那么 为什么快速幂的时间复杂度为O(log n)呢？因为我们首先要预处理出log k个数据，对于a的k次方，我们预处理a的2^0，a的2^1,....，a的2^log k，并且可以看出每一个数都是前一个数的平凡，我们直接累积就可以处理出来。

         然后，我们如何将a^k拆成我们预处理的值呢？我们可以将a^k拆成a的2^x1, .... ,a的2^xt的乘积，也等于a的2^x1 + 2^x2 + ... + 2^xt,这样我们就可以发现，我们将k转化成二进制，将对应1的预处理好的数据进行计算即可。这样我们只用花费O(log n)预处理数据，O(1)计算就可以得出答案。

         示例，4^5 mod 10, 我们预处理出 4 的 2^0, 4的2^1，4的2^2，然后将4^5拆解，5的二进制表示为101，即取出4 的 2^0和4的2^2相乘得到结果。

 875. 快速幂 - AcWing题库

给定 n 组 ai,bi,pi，对于每组数据，求出 ai ^ bi mod pi 的值。

输入格式

第一行包含整数 n。

接下来 n 行，每行包含三个整数 ai,bi,pi。

输出格式

对于每组数据，输出一个结果，表示 ai ^ bi mod pi  的值。

每个结果占一行。

数据范围

1≤n≤100000,
1≤ai,bi,pi≤2×1e9

输入样例：

2
3 2 5
4 3 9

输出样例：

4
1

#include<iostream>using namespace std;typedef long long LL;int qmi(int a, int b, int p)
{LL res = 1 % p;while(b){if(b & 1) res = res * a % p;a = (LL)a * a % p;b >>= 1;}return res;
}int main()
{int n;cin >> n;while(n--){int a, k, p;cin >> a >> k >> p;cout << qmi(a, k, p) << endl;}return 0;
}

876. 快速幂求逆元 - AcWing题库

         快速幂加上费马定理(假如p是质数，且gcd(a,p)=1（a和p互质），那么 a^(p-1)  ≡ 1（mod p），即 ( a^(p-1) )%p = 1)的运用，无解的情况为两数不互质，即a为p的倍数，否则我们一定可以通过费马定理构造出来一个解

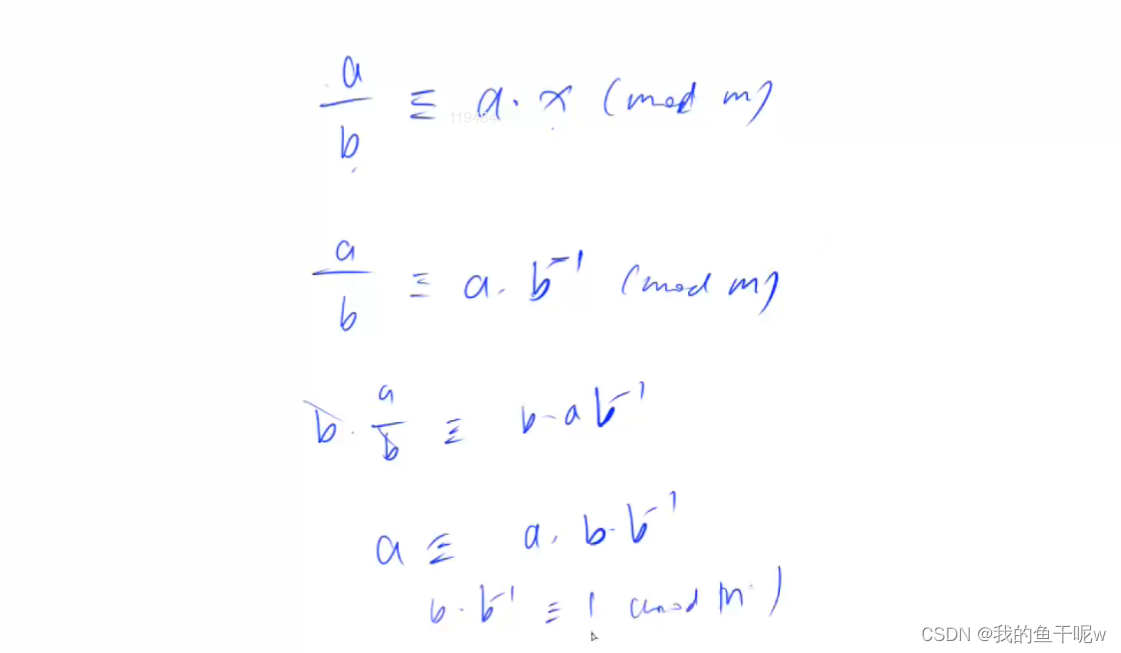
给定 n 组 ai,pi，其中 pi 是质数，求 ai 模 pi 的乘法逆元，若逆元不存在则输出 impossible。

注意：请返回在 0∼p−1 之间的逆元。

输入格式

第一行包含整数 n。

接下来 n 行，每行包含一个数组 ai,pi，数据保证 pi 是质数。

输出格式

输出共 n 行，每组数据输出一个结果，每个结果占一行。

若 ai 模 pi 的乘法逆元存在，则输出一个整数，表示逆元，否则输出 impossible。

数据范围

1≤n≤1e5,
1≤ai,pi≤2∗1e9

输入样例：

3
4 3
8 5
6 3

输出样例：

1
2
impossible

#include<iostream>
#include<algorithm>using namespace std;typedef long long LL;int qmi(int a, int b,int p)
{LL res = 1;while(b){if(b & 1) res = (LL) res * a % p;b >>= 1;a = (LL) a * a % p;}return res;
}int main()
{int n;cin >> n;while(n--){int a,p;cin>>a>>p;if(a % p == 0) cout << "impossible" << endl;else cout << qmi(a,p - 2,p) << endl;}return 0;
}