偏振光的描述：stokes参量（一）

对于一束完全偏振辐射（椭圆偏振波），如何描述其偏振状态？
圆偏振波和线偏振波都是椭圆偏振波的特例。

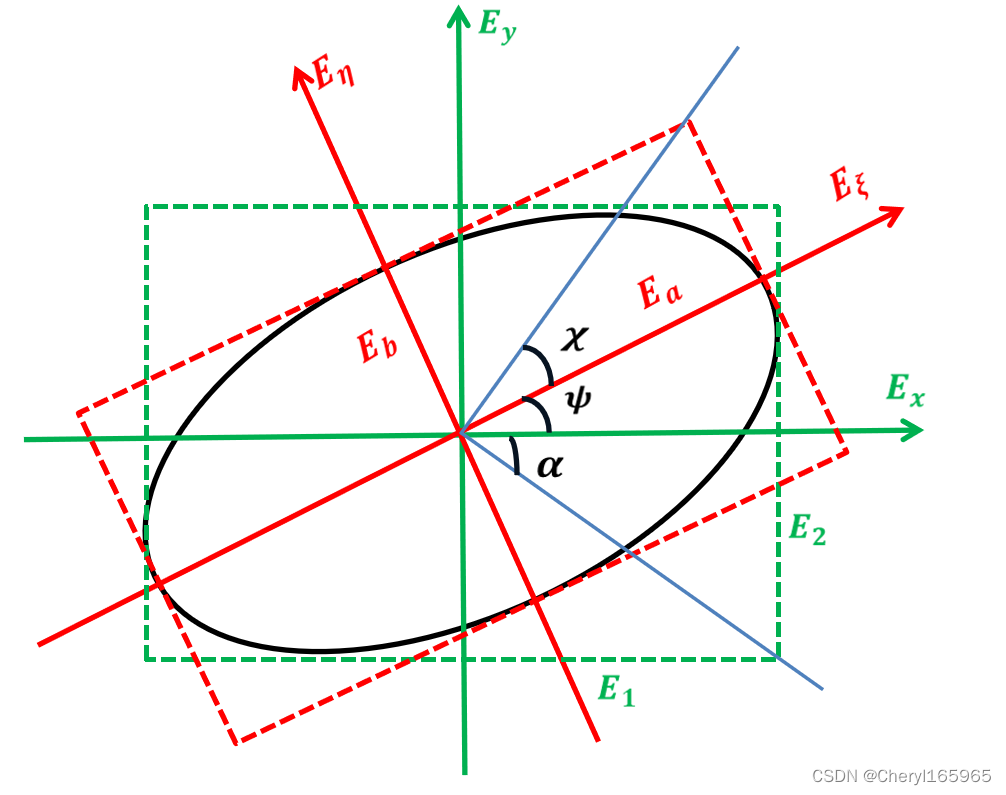
如下图所示为一椭圆偏振波，由屏幕内向屏幕外传播。
该波的瞬时场强可以表示为 $\mathbf{E}={\mathbf{E}}_1+{\mathbf{E}}_2$

${\mathbf{E}}_1(t)={\mathbf{e}}_1{a}_{1}cos(\omega t-{\delta }_1)$
${\mathbf{E}}_2(t)={\mathbf{e}}_2{a}_{2}cos(\omega t-{\delta }_2)$

因此，一旦给出$(a_1,a_2,{\delta }_1,{\delta }_2)$就唯一确定了一支椭圆偏振光及其全部偏振特性：强度${ϵ}^2=({\mathbf{E}}_1+{\mathbf{E}}_2{)}^2\equiv I$，方位角$\psi$，旋向及长短轴比（扁率）

当${\delta }_1={\delta }_2$时，表示线偏振光，偏振方向角(E与x轴夹角) $tg\theta =a_2/a_1$；
当$a_1=a_2$ 且 $\delta ={\delta }_1-{\delta }_2=\pm \pi /2$时，上式为圆偏振，$\pi /2$右旋，$-\pi /2$右旋。

坐标变换，将图中（x，y）转个$\psi$角到新的坐标系$（\eta ,\xi ）$，则

${\mathbf{E}}_{\mathbf{a}}(t)={ϵ}_{0}cos\chi cos(\omega t)$
${\mathbf{E}}_{\mathbf{b}}(t)=-{ϵ}_{0}sin\chi sin(\omega t)$

$({ϵ}_0，\psi ,\chi )$描述了同一组偏振特征，可相互转换。

用$(a_1,a_2,{\delta }_1,{\delta }_2)$描述偏振是非常理所当然的事情，但是实测中是很难测量初相位振幅什么的（至少单镜是这样），因此重新定义四个参量——stokes参量，来描述与$(a_1,a_2,{\delta }_1,{\delta }_2)$等效的偏振特性！

先引入stokes参量的定义，说明它是如何描述偏振状态的，如何引入描述的放在后面。

$I\equiv a_1^2+a_2^2={ϵ}_0^2$
$Q\equiv a_1^2-a_2^2$
$U\equiv 2a_1{a}_{2}cos({\delta }_2-{\delta }_1)$
$V\equiv 2a_1{a}_{2}sin({\delta }_2-{\delta }_1)$

$（I,Q,U,V）$为强度量纲，便于实测。测定出四参量后，反解出$(a_1,a_2,{\delta }_1,{\delta }_2)$，完全定出偏振特性$({ϵ}_0,\psi ,\chi )$

${ϵ}_0=\sqrt{I}$， $sin(2\chi )=V/I$， $tg(2\psi )=U/Q$

$I^2=Q^2+U^2+V^2$

I 代表椭圆偏振强度；
V决定$\chi$的数值，即决定椭圆偏振光的旋转方向和长短轴比；
U,Q 关系椭圆偏振光的长轴方位角$\psi$

知道全部偏振性质，也可以求解出stokes参量

$I={ϵ}_0^2$
$Q=Icos2\chi cos2\psi$
$U=Icos2\chi sin2\psi$
$V=Isin2\psi$

四参量的实测办法-引入

测量方向强度$I(\psi ,\eta )$