本文翻译自https://naokishibuya.medium.com/demystifying-kl-divergence-7ebe4317ee68

        KL散度中的KL全称是Kullback-Leibler，分别表示Solomon Kullback和Richard A.Leibler这两个人。

一、KL散度的定义

        KL散度表明概率分布Q和概率分布P之间的相似性，由交叉熵减去熵得到

        交叉熵和熵的计算如下

        代入到KL散度中，则

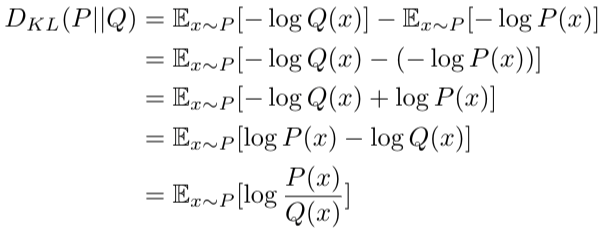
        上式中，期望可以表示成离散的求和，连续的求积分方式

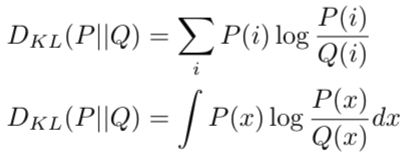
        这种两个概率间的相似性，是否衡量的是这两个概率的距离呢？要回答这个问题，先看KL散度的几个属性。

二、KL散度是非负的

        简单的证明如下：

• 如果P=Q，则

• 否则，则

        这是由于时，交叉熵是大于熵的，因为熵是最小平均编码长度。

三、KL散度是非对称的

        由于交叉熵是非对称的，所以交叉熵减去熵得到的KL散度也是非对称的

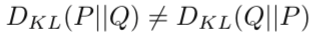
        由于距离指标是对称的，所以KL散度不是个距离衡量指标。通过下面的例子进行一个直观上的解释。假设有下面这样的概率分布P：

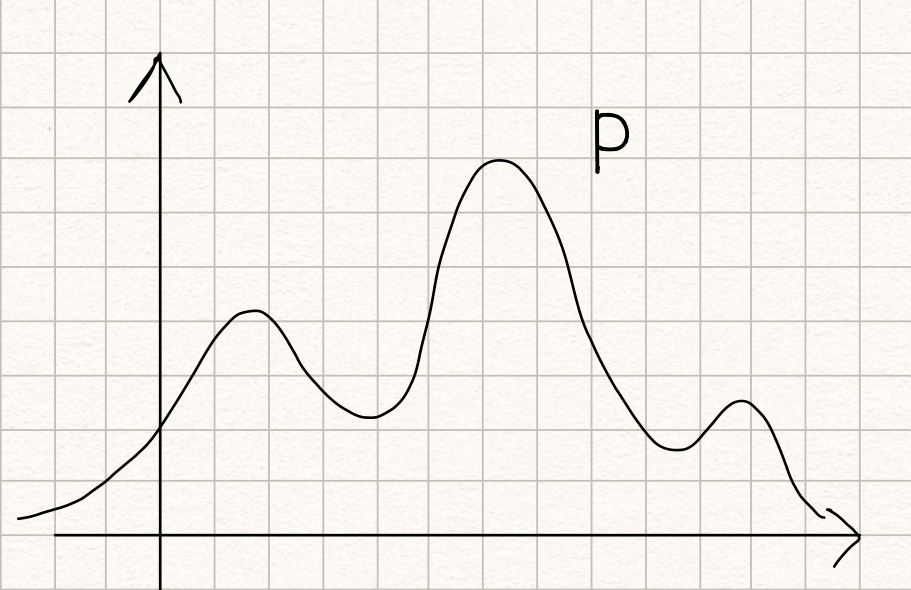
        然后用一个正态分布Q来近似P，如下所示：

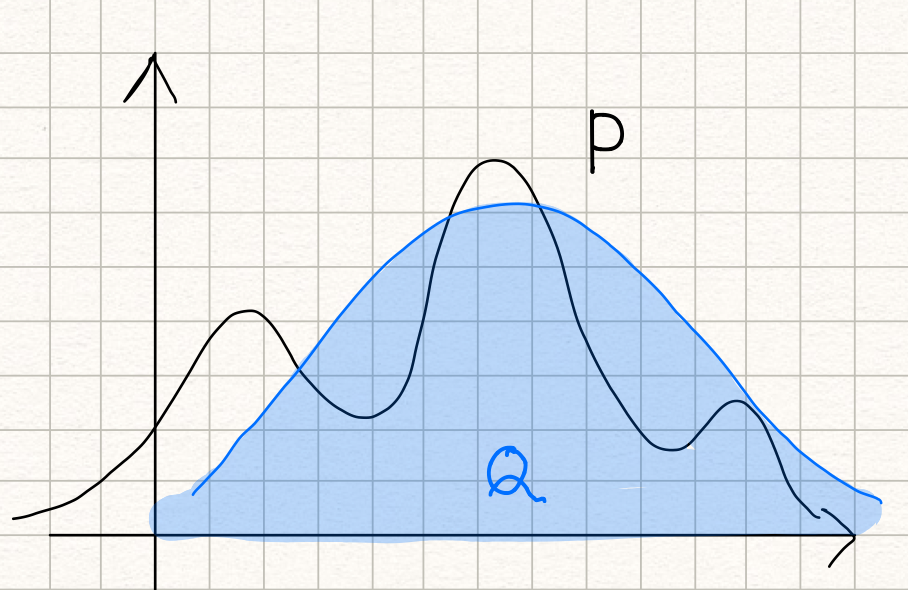
        由此可见，KL散度表示的是用概率分布Q来近似真实概率分布P时存在的误差。

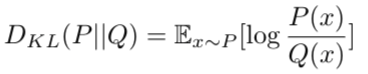
        如果将P和Q做一个交换，用概率分布P来近似概率分布Q，如下所示：

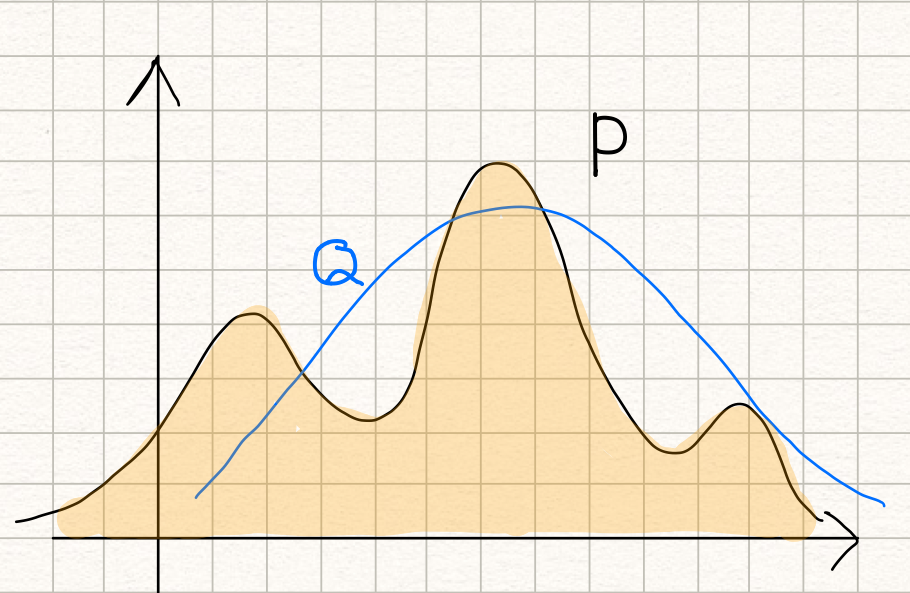
        此时，KL散度表示的是用概率分布P来近似真实概率分布Q时存在的误差。

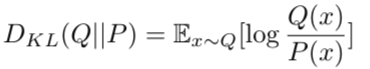
        由此可见，两者虽然表示都是概率分布P与概率分布Q之间的相似误差，但两个KL散度的结果是完全不同。

四、建模真实分布

        通过KL散度，可以用已知的常用分布，如正态分布、二项分布等，来建模真实分布。通过KL散度，可以求解机器学习模型，如得到模型的参数等，来建模机器学习对应的真实分布。

五、变分自编码器

        KL散度在变分自编码器中也有使用，用来让隐变量尽量接近正态分布，从而能从正态分布中抽样得到隐变量。于是，在变分自编码器的损失函数中加入了KL散度。

六、额外的一些数学问题

        1）当p趋于0时，存在如下公式

        如果p>0，q=0，则KL散度为无穷大，因为

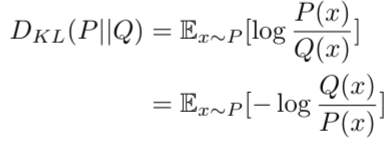
        所以

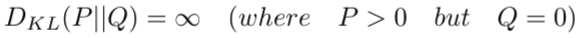
七、似然比

        另外一种从概率分布描述KL散度的方式是如下的似然比：

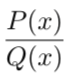
        从前面KL散度的定义中，可以看到这个似然比是KL散度中的一部分，即对数里的部分

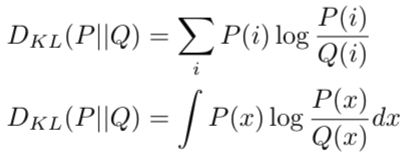
参考

https://naokishibuya.medium.com/demystifying-kl-divergence-7ebe4317ee68
https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence