1 文章信息
文章题为“A Learning Based Intelligent Train RegulationMethod With Dynamic Prediction forthe Metro Passenger Flow”,该文于2023年发表至“IEEE TRANSACTIONS ON INTELLIGENT TRANSPORTATION SYSTEMS”。文章的核心观点是提出了一种基于学习的智能列车调节方法,该方法通过动态预测地铁乘客流来优化列车的运行。
2 摘要
随着城市化的加速,动态乘客流对实际列车运营的影响日益增长。在本文中,我们提出了一种基于学习的智能列车调节方法,该方法具有动态乘客流预测功能。为了捕捉动态地铁乘客流的特征,建立了一个卷积神经网络来实时预测从空间和时间两个维度的乘客流。由于实际乘客流数据的不足限制了预测精度,构建了一个深度卷积生成对抗网络来生成与原始乘客流数据集具有相同分布的数据。然后,考虑到动态乘客流对列车运营的影响和列车容量限制,将动态列车调节问题表述为一个多阶段最优控制问题,目标函数是最小化列车牵引能耗和乘客的总旅行时间。为了在每个决策步骤中有效地获得最优调节策略,提出了一种深度Q网络算法来解决制定的问题,从而避免了由于过度状态空间引起的维数爆炸。数值实验表明了我们提出的算法和模型的高效性和有效性。
3 引言
现有的列车调度方法主要是基于静态乘客流数据设计的,例如假设客流遵循某种固定分布,直接使用某一天的历史乘客流数据。然而,客流的分布具有随机性,在时间和空间上都会出现波动,这可能会降低列车调度方案的性能。因此,有必要设计一种能够适应动态乘客流需求的智能列车调度策略。
当训练数据量足够大时,可利用深度学习模型进行客流预测。然而,由于隐私保护和利益冲突的原因,不同城市轨道交通管理部门的乘客流数据很少共享。因此,可采用数据增强的方法弥补这一缺陷,本文利用GAN来实现数据增强。
文章贡献之处在于:
1、构建CNN网络实时预测乘客到达率和下车率。此外,为了缓解训练数据不足对CNN模型精度的影响,引入了一种基于GAN的数据生成方法来实现数据增强。
2、为了求解具有动态参数更新的非线性最优控制问题,利用预测的实时乘客到达率和下车率来训练基于DQN的算法,以获得理想的调节策略。该算法既避免了状态空间过大带来的维数爆炸,又满足了列车运行调控的高实时性要求。
4 问题定义
设列车集合为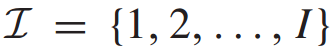 ,车站集合为
,车站集合为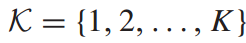 ,假设所有列车在地铁线路上按顺序向一个方向运行,不允许超车和两车平行运行。假设在列车i在车站k停靠期间,到达的乘客会乘坐下一辆列车。此外,所有乘客都应该遵循先进先出的原则。
,假设所有列车在地铁线路上按顺序向一个方向运行,不允许超车和两车平行运行。假设在列车i在车站k停靠期间,到达的乘客会乘坐下一辆列车。此外,所有乘客都应该遵循先进先出的原则。
(1)列车动态运行模型
设列车i到达k站的时间为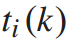 ,列车在k到k+1站的运行时间为
,列车在k到k+1站的运行时间为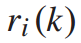 ,列车在k站的停站时间为
,列车在k站的停站时间为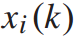 ,其中,停站时间为决策变量,当
,其中,停站时间为决策变量,当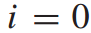 时设
时设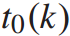 为车站k的开通时间。则
为车站k的开通时间。则
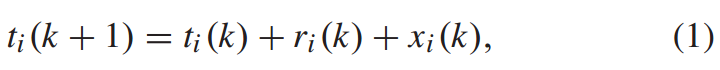
列车停站时间需要满足最大最小的约束,即:
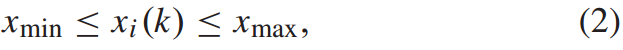
同时,列车在铁路上行驶时,不允许后面的列车超过前面的列车,列车i−1到达时间与列车i到达时间之间的车头距应满足以下约束条件:
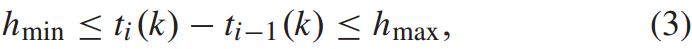
其中,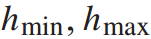 表示列车车头距的最大最小值。
表示列车车头距的最大最小值。
列车在始发站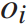 的发车时间为:
的发车时间为:

在前后两辆列车达到k站的时间间隔内,客流人数为:
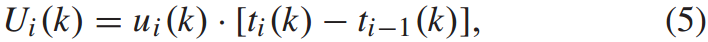
其中,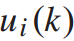 为第i辆列车到达k站时的乘客到达率。
为第i辆列车到达k站时的乘客到达率。
下车率与上车人数成正比,在k站下车i列车的乘客人数为:
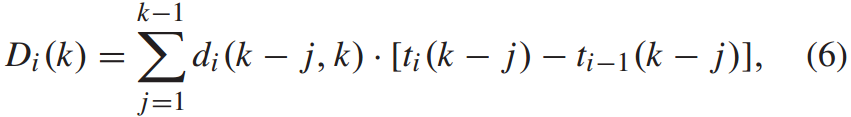
其中,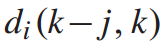 表示在k−j站乘坐列车i并在k站下车的乘客的下车率。
表示在k−j站乘坐列车i并在k站下车的乘客的下车率。
设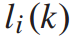 为列车i到达k车站时的可变乘客数,C为列车容量。
为列车i到达k车站时的可变乘客数,C为列车容量。
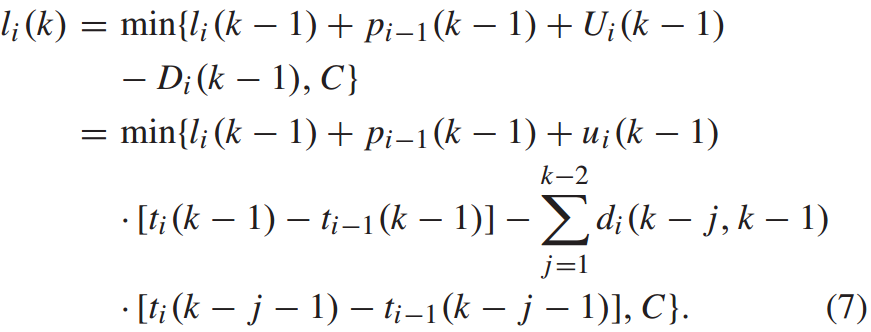
设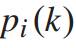 为在k车站未能登上列车i的乘客数:
为在k车站未能登上列车i的乘客数:
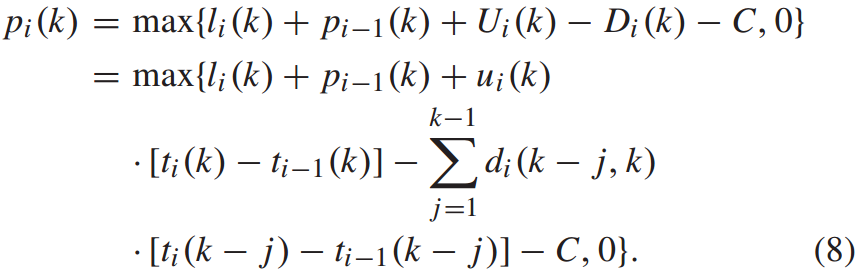
其中,在公式7和公式8中都以逗号分为两部分,公式7中,第一部分表示不计列车运力,列车i到达k站时的理想乘客人数。如果第一部分小于列车的载客量,那么所有到达车站的乘客都可以上车。如果第一部分大于列车容量,则列车只能容纳最大容量。公式8中,第一部分的前四项之和大于列车载客量,则可能有部分乘客需要等待下一辆列车,剩余乘客的数量将等于前四项减去列车载客量。否则,没有乘客留下,则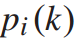 为0。
为0。
(2)动态客流预测模型
文章利用CNN进行动态客流预测,采用单步预测。其过程可描述为:

其中f为卷积神经网络模型,n为时间步,x、y、z为各站历史客流数据,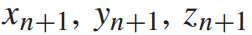 为各站下一时刻客流预测值。
为各站下一时刻客流预测值。
(3)目标函数
文章的目标是最小化列车牵引能耗和乘客总旅行时间。设S为旅客的总出行时间,包括旅客在车时间和在站台等候时间,可表示为:

其中,α1为旅客在车时间权值,α2为旅客等待时间权值。
总旅客在车时间S1由列车运行时间和列车停留时间组成,如下:
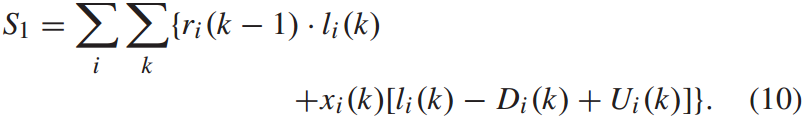
旅客在车总时间包括两个部分。第一部分表示列车在两站之间运行时乘客在列车上的总时间。第二部分表示列车到站时乘客在列车上的总时间,其中乘客人数可以通过列车到站时已经在列车上的乘客人数减去下车的乘客人数加上上车的乘客人数来计算。
乘客在站台的总等候时间S2也由两部分组成。第一部分是列车i和列车i−1到站时间内到达车站的旅客的等待时间,第二部分是被末班车抛下,需要等待下一班车的旅客的等待时间,如下。
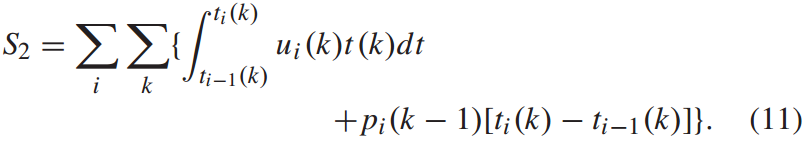
列车牵引能耗可表示为:
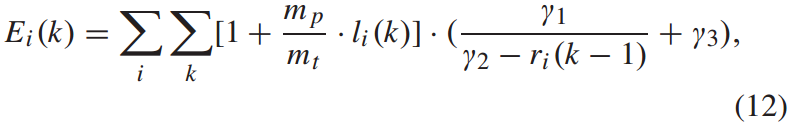
其中,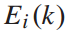 为列车牵引能耗,
为列车牵引能耗,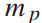 乘客平均重量,
乘客平均重量,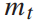 为列车重量,
为列车重量,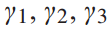 为列车牵引能耗系数。
为列车牵引能耗系数。
综上,目标函数可设为:
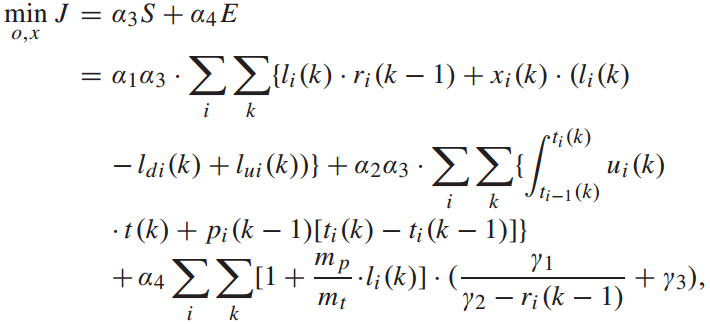
其中,α3为乘客出行时间权重,α4为能耗权重。
(4)优化模型
根据以上描述,优化模型如下:
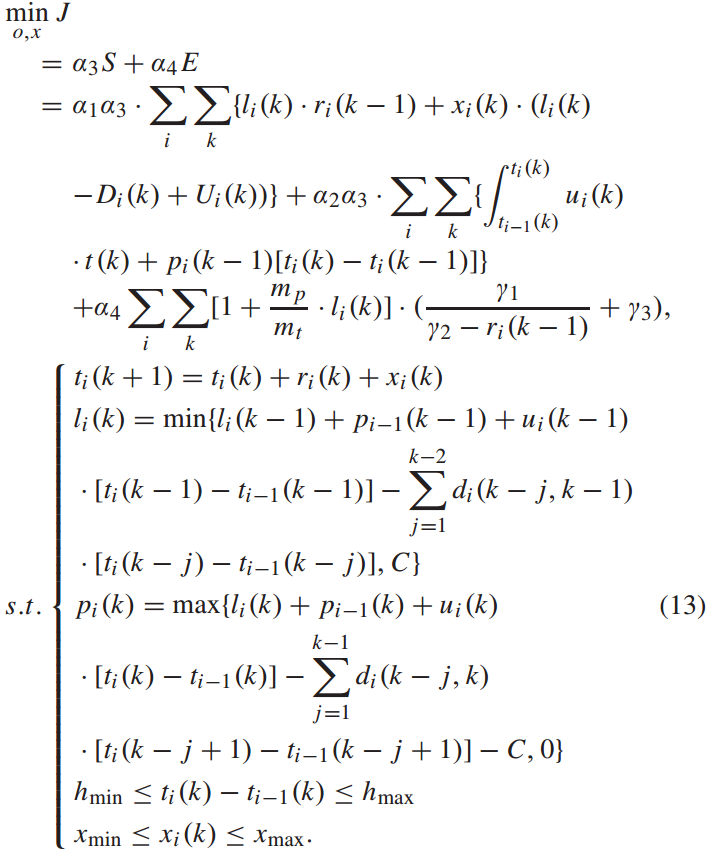
该问题是一个非线性动态规划问题,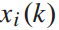 和
和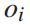 为决策变量,
为决策变量,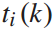 、
、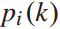 、
、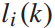 为状态变量,前三个方程是状态转移方程。第五个不等式方程是决策变量
为状态变量,前三个方程是状态转移方程。第五个不等式方程是决策变量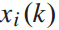 的约束。由公式4可知,列车i在始发站
的约束。由公式4可知,列车i在始发站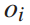 的发车时间与到达时间
的发车时间与到达时间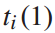 和停站时间
和停站时间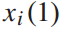 有关,因此,第四个和第五个不等式方程是决策变量
有关,因此,第四个和第五个不等式方程是决策变量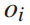 的约束。
的约束。
5 基于GAN数据生成的客流预测方法
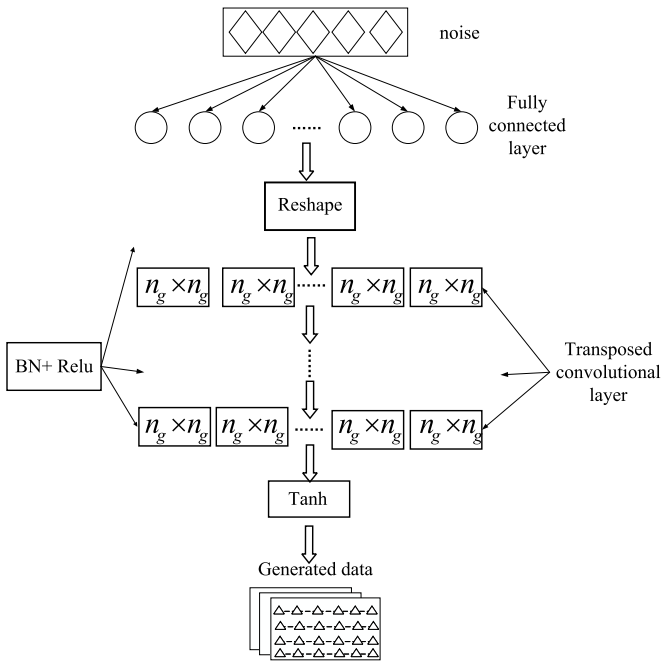
文章提到原始的GAN网络生成的数据质量令人不满意,于是提出了深度卷积生成对抗网络DCGAN,用卷积神经网络代替了生成器和鉴别器,使得生成的样本质量和模型的收敛速度都有了明显的提高。其结构如图所示。文章提到数据量偏少的问题,可经过该网络获得真实的客流数据,弥补该问题。
6 基于卷积神经网络的客流预测
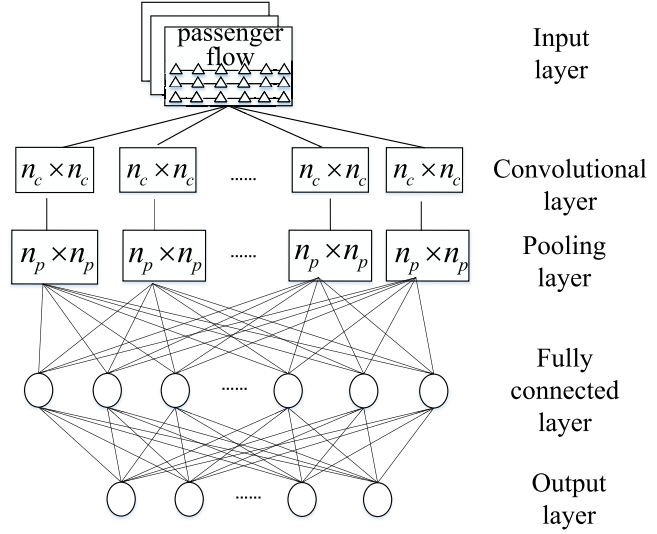
在实验中发现,使用历史客流数据来训练调节模型并不能很好地匹配车站动态客流的特征。因此,引入卷积神经网络来实时预测客流量进而计算乘客到达率和下车率。具体来说,模型使用历史乘客流量数据作为输入,预测接下来时刻的客流量。这些预测的乘客流量数据包括了不同站点的信息,允许模型同时预测多个站点的乘客流量。然后,利用这些预测的乘客流量数据,可以计算出每个站点的乘客到达率(即单位时间内到达的乘客数量)和下车率(即单位时间内离开列车的乘客数量)。这些率随后被用作动态火车调节模型中的参数,以此来优化火车的运行时间表和站台停留时间,减少能耗,并改善乘客的出行体验。下图为模型结构。
7 列车智能调度算法设计
强化学习是一种让计算机通过不断的尝试从错误中学习,最终找到规则并完成目标的方法。在强化学习算法中,决策者与环境相互作用。通过观察环境s的状态,决策者采取行动a,然后环境返回给决策者奖励r和新状态s’,然后决策者根据奖励采取新行动a'。决策者的目标是使回报最大化。
在提出的列车运行实时调整问题中,决策者是每列列车。动作为列车i在始发站的出发时间和列车i在k站的停留时间。由式(4)可知,列车i在始发站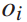 的出发时间与到达时间
的出发时间与到达时间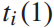 和停留时间
和停留时间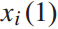 有关。因此,我们将动作
有关。因此,我们将动作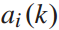 定义为:
定义为:
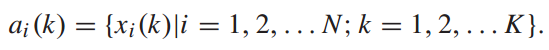
另外,将第i次列车在k站的奖励定义为列车牵引能耗、乘客在车时间和乘客在站台等待时间之和,表示为:
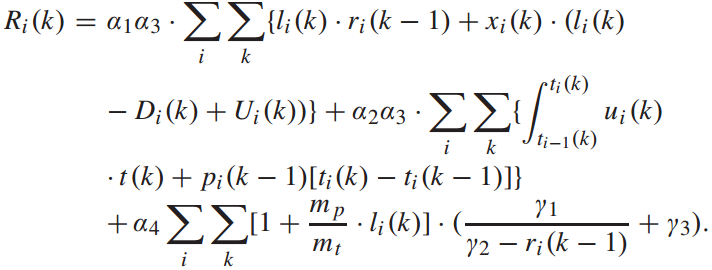
由于模型的目标是使列车牵引能耗和乘客总出行时间最小,所以需要找到一个使所有车站所有列车的总奖励最小的行动策略:
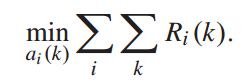
强化学习引入一个价值函数来评估某一行动策略所获得的总收益。价值函数可以根据当前状态的行为策略预测未来累积收益的期望。为了评估每个动作的值,定义动作值函数的Bellman方程:
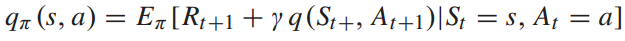
Q学习是一种重要的基于值函数的强化学习方法。它以表格的形式存储每个动作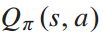 的值函数。Q-learning的迭代实际上是对每个状态-动作的Q值表的更新。当Q表最终收敛时,决策者使用贪心策略根据值函数表选择行动:
的值函数。Q-learning的迭代实际上是对每个状态-动作的Q值表的更新。当Q表最终收敛时,决策者使用贪心策略根据值函数表选择行动:
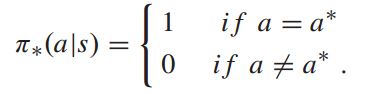
贪心策略是一种确定性策略,它只选择使价值函数最优的行为。如上所述,最优行为是使价值函数最小化。因此,我们让:
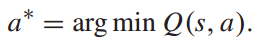
但是,如果状态空间的维数非常大,或者状态空间是连续的,则值函数不能存储在表中。在我们提出的列车运行实时调整优化模型中,状态变量是一个三维向量,表格强化学习方法不再适用。
深度Q网络算法(DQN)将深度学习与Q学习相结合,允许深度神经网络近似Q函数,从而完美地解决了维数过大问题。因此,选择DQN来处理列车运行实时调整模型。DQN的结构如图所示。用来逼近Q函数的神经网络称为Q网络。DQN算法值函数的更新是参数θ的更新。采用随机梯度下降法,使目标Q值与待逼近Q值之间的差值最小,形成为:
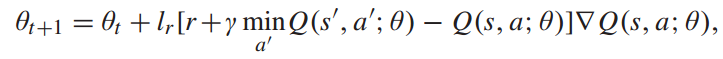
其中,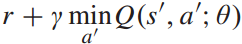 是目标值。
是目标值。
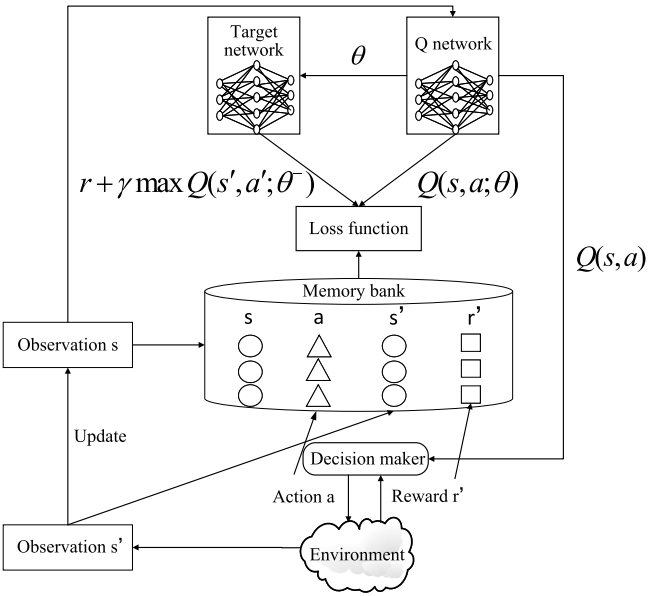
然而,用于计算目标Q值的参数与梯度更新中要逼近的值函数相同,这会导致数据之间的相关性,降低训练的稳定性。因此,提出了一种双重网络结构。设计一个目标网络来计算目标Q值。目标网络的结构与Q网络相同。Q网络的参数θ每步更新一次,目标网络的参数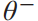 每F步更新一次。当更新目标网络的参数时,Q网络复制它的参数θ到目标网络。然后,将值函数更新为:
每F步更新一次。当更新目标网络的参数时,Q网络复制它的参数θ到目标网络。然后,将值函数更新为:
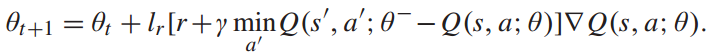
DQN设计了一个重放缓冲区来打破训练数据之间的相关性。决策者按时间顺序将当前状态s、当前动作a、下一个状态s'和奖励r'存储到重放缓冲区中。然后,采用均匀随机抽样的方法从回放缓冲区中提取数据进行神经网络训练,降低了数据之间的相关性,稳定了训练结果。列车运行实时调整DQN的训练如以下算法所示。

根据以上研究,列车运行动态调整过程可归纳为算法3。首先基于DCGAN,生成与原始客流数据分布相同的数据,并将生成的数据作为CNN的训练集。然后将CNN预测的客流数据作为算法2的参数,使用算法2训练DQN。最后,基于训练好的DQN进行列车运行调整。

8 实验
作者做了三组实验,第一组实验验证了所提出的数据增强模型DCGAN的有效性,第二组实验比较了RNN、LSTM、CNN和基于DCGAN的卷积神经网络模型的预测结果,以证明该模型的优越性。最后一组实验将基于经验的DQN方法的结果与设计的基于动态预测客流的DQN方法的结果进行了对比,验证了基于动态预测客流的DQN方法的性能。考虑推文篇幅,主要介绍第三组实验的内容。作者使用具有13个站的北京地铁13号线作为实验对象。
在这组实验中,使用基于经验的方法为方法1、基于固定客流的方法为方法2、基于固定客流的DQN方法为方法3、基于动态客流设计的DQN方法为方法4。
方法1中列车运行时间和停留时间的调度均基于北京地铁13号线的实际运行数据;方法2和方法3中,由于仅以列车停留时间为优化变量,列车运行时间也以实际运行数据为基础,固定的客流参数采用地铁13号线2014年3月平均客流计算。方法4采用本文提出的CNN模型对动态客流参数进行预测。我们首先观察方法3和方法4的值函数的收敛过程。然后,利用本文提出的方法编制列车运行时刻表。最后,比较了四种列车运行方案的目标值、牵引能耗、乘客在车时间和乘客候车时间。
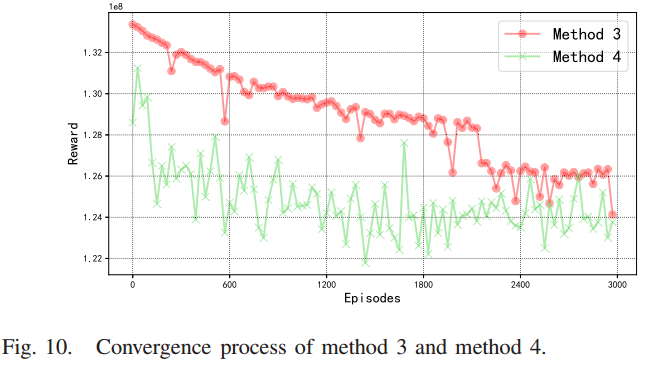
该图显示了方法3和方法4的收敛过程。DQN模型的训练过程是不稳定的。如果迭代次数不够,模型将不能很好地收敛。此外,在迭代开始时,模型波动较大。随着迭代次数的增加,奖励将逐渐收敛,最终在最优奖励附近略有波动。
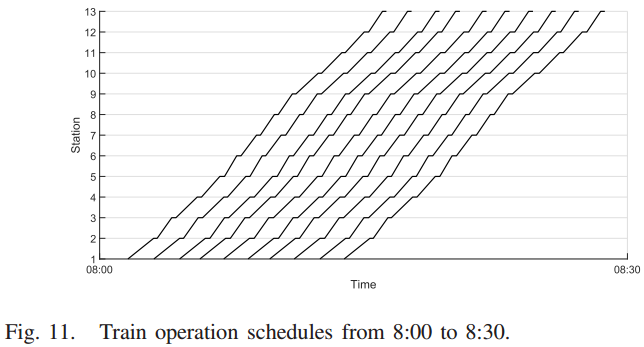
下图为基于方法4绘制的列车运行时刻表。由于每列列车在各站停留时间是一个有待优化的变量,因此列车i与列车i−1在k站到达时间之间的车头距是不同的,这就意味着运行时间是不规律的。
下表给出了四种列车运行调度方法对应的计算结果。比较了三种列车运行方案的目标值、牵引能耗、乘客在车时间、乘客等待时间和决策时间等因素。目标值按式(13)计算,牵引能耗按式(12)计算,旅客在车时间按式(10)计算,旅客候车时间按式(11)计算。
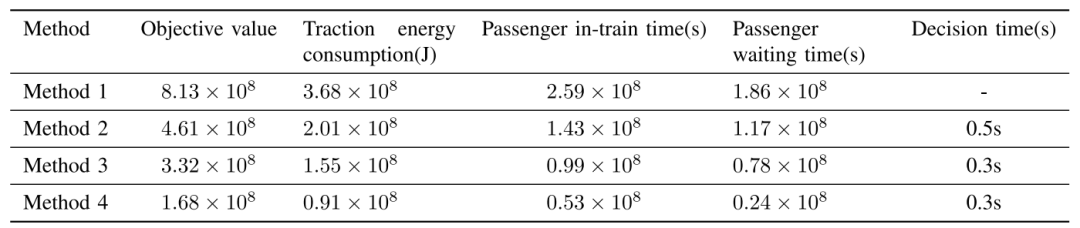
可以看出,采用方法绘制的列车运行时刻表的目标值、牵引能耗、旅客在车时间和旅客候车时间均最高。即根据经验设计列车运行时刻表是不合理和不科学的,这会增加能源消耗,降低服务水平。
通过对比方法2和方法3,可以发现方法2的训练次数要比方法3少得多。这是因为DQN方法需要训练神经网络,这比训练表要困难得多。然而,当比较优化结果时,方法3比方法2要好得多,这是因为使用ADP算法需要离散化训练状态来降低维数,从而降低了模型的精度。DQN模型采用Q神经网络对列车停留时间进行决策,不需要降低列车状态维数。此外,我们还注意了方法的决策时间。可以观察到,当训练完成时,方法3的决策时间也小于方法2,这是因为方法2需要遍历整个表才能找到最优的训练停留时间,而方法3使用Q网络直接输出最优结果。
根据方法3和方法4比较,可以发现使用方法3制定的列车运行计划的确降低了列车牵引能耗和乘客总行程时间,但优化结果也不如方法4,这是由于方法3没有考虑动态客流的影响。采用方法4编制的列车运行时刻表的旅客总行程时间小于方法3,说明本文提出的方法4能更好地适应动态客流。此外,方法4大大降低了列车牵引能耗。并且采用方法4对列车发车时间和停留时间进行调整,可以在节约能源和提高乘客舒适度之间取得平衡。
9 结论
文章首先构建DCGAN模型,以生成足够的客流数据。然后,基于所提出的DCGAN生成的数据进行客流预测。建立了从空间和时间两个维度预测客流的CNN。根据预测的实时乘客上车率和下车率,提出了一种基于DQN的学习算法,计算列车调度策略,动态调整列车发车时间和停留时间,使列车牵引能耗和乘客总旅行时间最小。利用北京地铁13号线的运行数据对该方法进行了验证。仿真结果证明了该方法的有效性。