线性代数入门
线性代数(Linear Algebra)是数学的重要分支之一,广泛应用于工程、计算机科学、物理学、经济学等领域。它主要研究向量、矩阵及其在空间中的变换。对于程序员来说,掌握线性代数的基础知识能够帮助更好地理解数据处理、机器学习等应用中的数学原理。本文将为你介绍线性代数的基本概念和核心内容。
一、基本概念
1. 向量(Vector)
向量是线性代数的核心元素,它可以看作一个有序数列。向量可以用来表示几何中的点、物理中的力等。向量通常用小写字母表示,如 ( \mathbf{v} ) 表示一个向量:
[ \mathbf{v} = \begin{bmatrix} v_1 \ v_2 \ \vdots \ v_n \end{bmatrix} ]
其中,( v_1, v_2, \dots, v_n ) 是向量的分量。向量的维度由其分量的个数决定。例如,三维向量 ( \mathbf{v} = \begin{bmatrix} 1 \ 2 \ 3 \end{bmatrix} ) 有三个分量,属于三维空间。
2. 矩阵(Matrix)
矩阵是一个二维数组,由行(row)和列(column)组成。矩阵可以看作是多个向量的组合,广泛用于线性变换、方程求解等。矩阵通常用大写字母表示,如矩阵 ( A ):
[ A = \begin{bmatrix} a_{11} & a_{12} \ a_{21} & a_{22} \end{bmatrix} ]
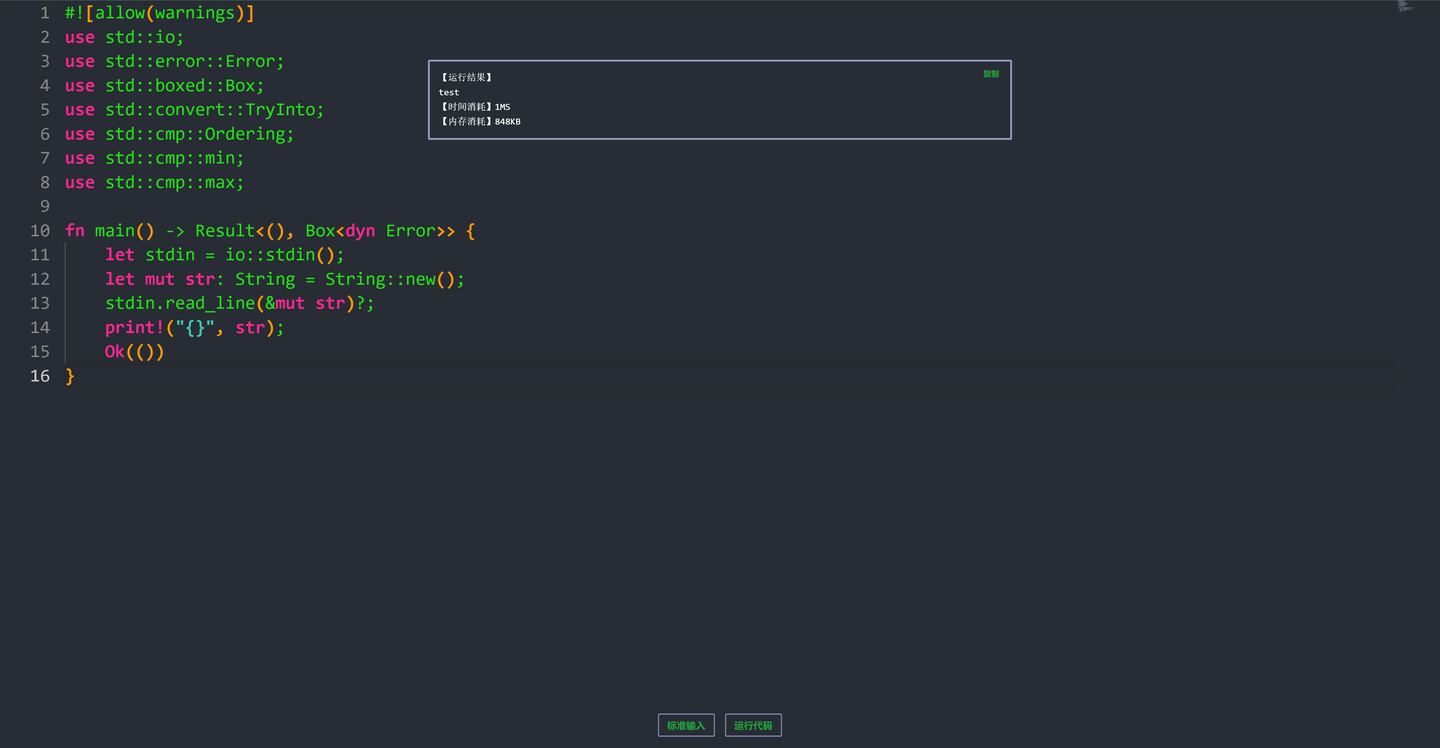
矩阵中的每个元素 ( a_{ij} ) 表示矩阵第 ( i ) 行、第 ( j ) 列的值。例如,矩阵 ( A ) 是一个 ( 2 \times 2 ) 矩阵,因为它有 2 行和 2 列。
3. 标量(Scalar)
标量是一个简单的数,可以是实数或复数。标量用于缩放向量或矩阵中的元素。举例来说,给定一个向量 ( \mathbf{v} = \begin{bmatrix} 2 \ 3 \end{bmatrix} ) 和标量 ( c = 2 ),标量与向量的乘法 ( c\mathbf{v} ) 为:
[ c\mathbf{v} = \begin{bmatrix} 2 \times 2 \ 2 \times 3 \end{bmatrix} = \begin{bmatrix} 4 \ 6 \end{bmatrix} ]
二、线性代数的核心运算
1. 向量加法
向量加法是指两个向量对应分量的逐项相加。假设 ( \mathbf{v_1} ) 和 ( \mathbf{v_2} ) 为两个向量:
[ \mathbf{v_1} = \begin{bmatrix} 1 \ 2 \end{bmatrix}, \mathbf{v_2} = \begin{bmatrix} 3 \ 4 \end{bmatrix} ]
向量加法 ( \mathbf{v_1} + \mathbf{v_2} ) 为:
[ \mathbf{v_1} + \mathbf{v_2} = \begin{bmatrix} 1 + 3 \ 2 + 4 \end{bmatrix} = \begin{bmatrix} 4 \ 6 \end{bmatrix} ]
2. 矩阵乘法
矩阵乘法是线性代数中最重要的运算之一。两个矩阵相乘时,遵循行乘列的规则。假设矩阵 ( A ) 和 ( B ) 为:
[ A = \begin{bmatrix} 1 & 2 \ 3 & 4 \end{bmatrix}, B = \begin{bmatrix} 5 & 6 \ 7 & 8 \end{bmatrix} ]
矩阵 ( A \times B ) 的结果是:
[
A \times B = \begin{bmatrix} 1 \times 5 + 2 \times 7 & 1 \times 6 + 2 \times 8 \ 3 \times 5 + 4 \times 7 & 3 \times 6 + 4 \times 8 \end{bmatrix} = \begin{bmatrix} 19 & 22 \ 43 & 50 \end{bmatrix}
]
3. 点积(Dot Product)
向量的点积是两个向量对应分量的乘积之和。给定两个向量 ( \mathbf{v_1} ) 和 ( \mathbf{v_2} ):
[ \mathbf{v_1} = \begin{bmatrix} 1 \ 2 \end{bmatrix}, \mathbf{v_2} = \begin{bmatrix} 3 \ 4 \end{bmatrix} ]
它们的点积为:
[ \mathbf{v_1} \cdot \mathbf{v_2} = 1 \times 3 + 2 \times 4 = 3 + 8 = 11 ]
点积是计算向量夹角和向量相似度的基础运算。
4. 行列式(Determinant)
行列式是一个与矩阵相关的标量,用于衡量矩阵是否可逆以及线性方程组是否有唯一解。对于一个 ( 2 \times 2 ) 矩阵 ( A ):
[ A = \begin{bmatrix} a & b \ c & d \end{bmatrix} ]
行列式 ( \det(A) ) 的计算公式为:
[ \det(A) = ad - bc ]
如果行列式不为 0,矩阵 ( A ) 是可逆的,否则矩阵不可逆。
三、线性代数的实际应用
1. 计算机图形学
在计算机图形学中,线性代数被广泛用于处理图像和三维模型的变换。通过矩阵的旋转、平移、缩放等操作,可以对三维物体进行各种变换,从而实现复杂的图形渲染和动画。
2. 机器学习
线性代数是机器学习的数学基础。在机器学习中,数据通常以矩阵和向量的形式表示,线性回归、神经网络等算法都依赖矩阵运算来进行模型训练和优化。
3. 物理模拟
物理中的许多模型,如力学系统、电路分析、量子力学等,都是通过线性方程组和矩阵描述的。线性代数提供了有效的工具来解决这些问题。
四、结语
线性代数是现代数学和应用科学的重要组成部分,涉及的概念和运算广泛应用于各个领域。掌握向量、矩阵及其基本运算,是深入学习高级数学、机器学习、物理模拟等领域的基础。希望本文能帮助你快速入门线性代数,为进一步的学习奠定坚实的基础。
推荐几款学习编程的免费平台
免费在线开发平台(https://docs.ltpp.vip/LTPP/)
探索编程世界的新天地,为学生和开发者精心打造的编程平台,现已盛大开启!这个平台汇集了近4000道精心设计的编程题目,覆盖了C、C++、JavaScript、TypeScript、Go、Rust、PHP、Java、Ruby、Python3以及C#等众多编程语言,为您的编程学习之旅提供了一个全面而丰富的实践环境。
在这里,您不仅可以查看自己的代码记录,还能轻松地在云端保存和运行代码,让编程变得更加便捷。平台还提供了私聊和群聊功能,让您可以与同行们无障碍交流,分享文件,共同进步。不仅如此,您还可以通过阅读文章、参与问答板块和在线商店,进一步拓展您的知识边界。
为了提升您的编程技能,平台还设有每日一题、精选题单以及激动人心的编程竞赛,这些都是备考编程考试的绝佳资源。更令人兴奋的是,您还可以自定义系统UI,选择视频或图片作为背景,打造一个完全个性化的编码环境,让您的编程之旅既有趣又充满挑战。
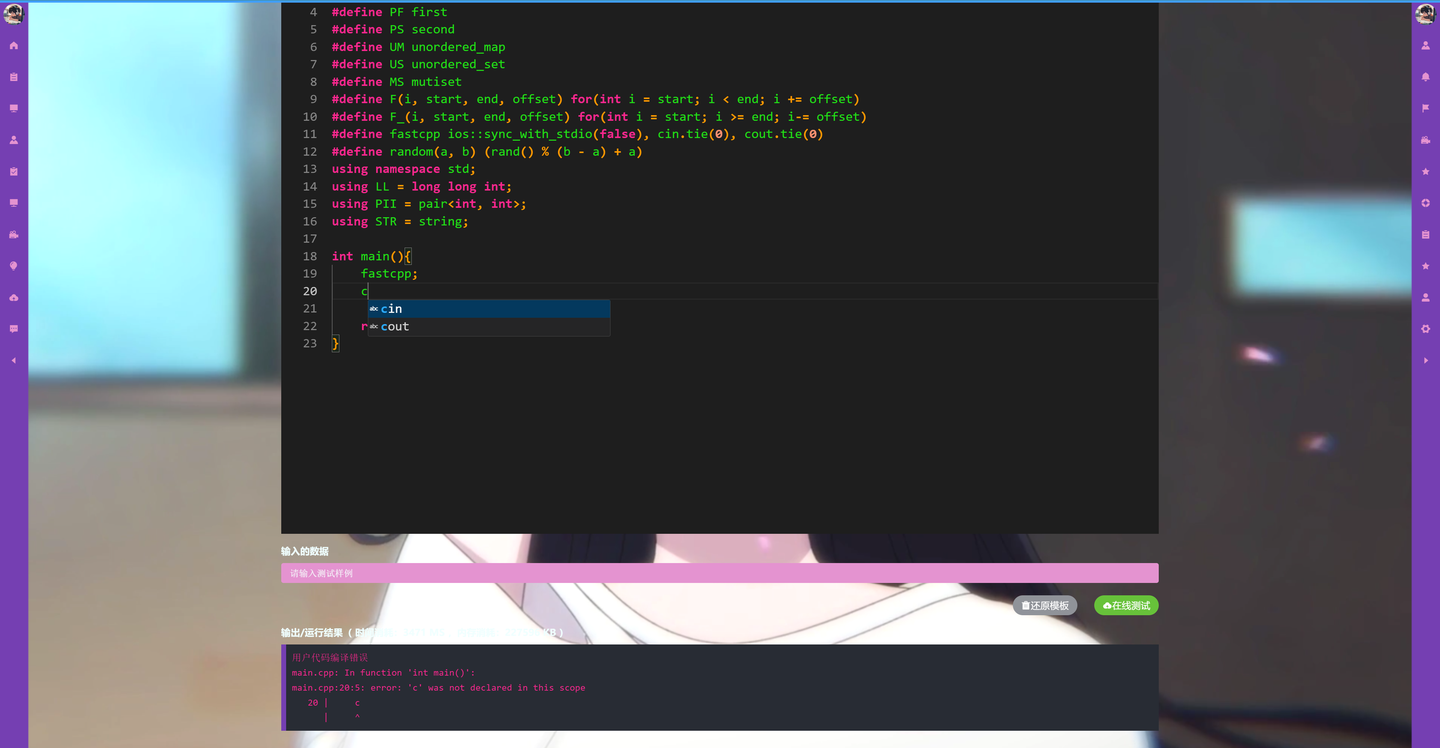
免费公益服务器(https://docs.ltpp.vip/LTPP-SHARE/linux.html)
作为开发者或学生,您是否经常因为搭建和维护编程环境而感到头疼?现在,您不必再为此烦恼,因为一款全新的免费公共服务器已经为您解决了所有问题。这款服务器内置了多种编程语言的编程环境,并且配备了功能强大的在线版VS Code,让您可以随时随地在线编写代码,无需进行任何复杂的配置。
随时随地,云端编码
无论您身在何处,只要有网络连接,就可以通过浏览器访问这款公共服务器,开始您的编程之旅。这种云端编码的便利性,让您的学习或开发工作不再受限于特定的设备或环境。
丰富的编程语言支持
服务器支持包括C、C++、JavaScript、TypeScript、Go、Rust、PHP、Java、Ruby、Python3以及C#等在内的多种主流编程语言,满足不同开发者和学生的需求。无论您是初学者还是资深开发者,都能找到适合自己的编程环境。
在线版VS Code,高效开发
内置的在线版VS Code提供了与本地VS Code相似的编辑体验,包括代码高亮、智能提示、代码调试等功能,让您即使在云端也能享受到高效的开发体验。
数据隐私和安全提醒
虽然服务器是免费的,但为了保护您的数据隐私和安全,我们建议您不要上传任何敏感或重要的数据。这款服务器更适合用于学习和实验,而非存储重要信息。
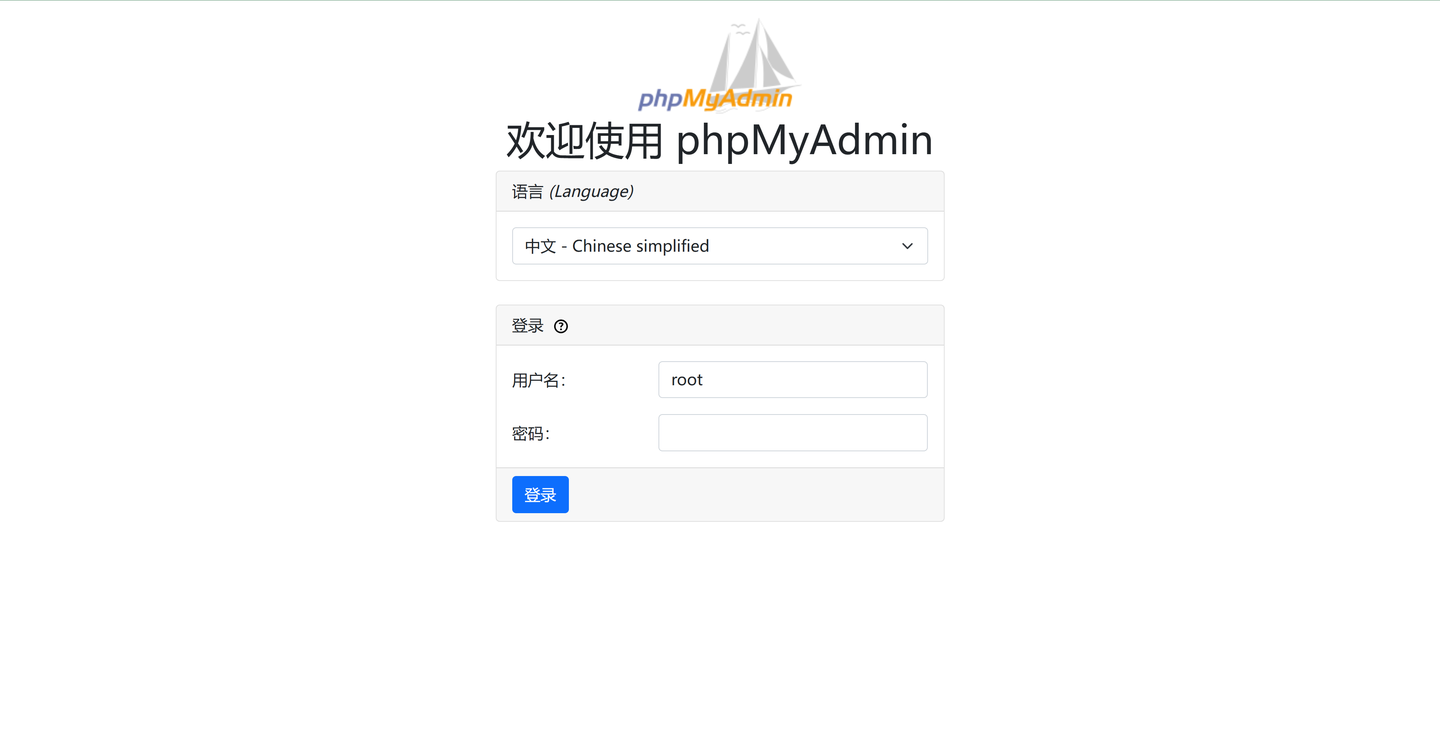
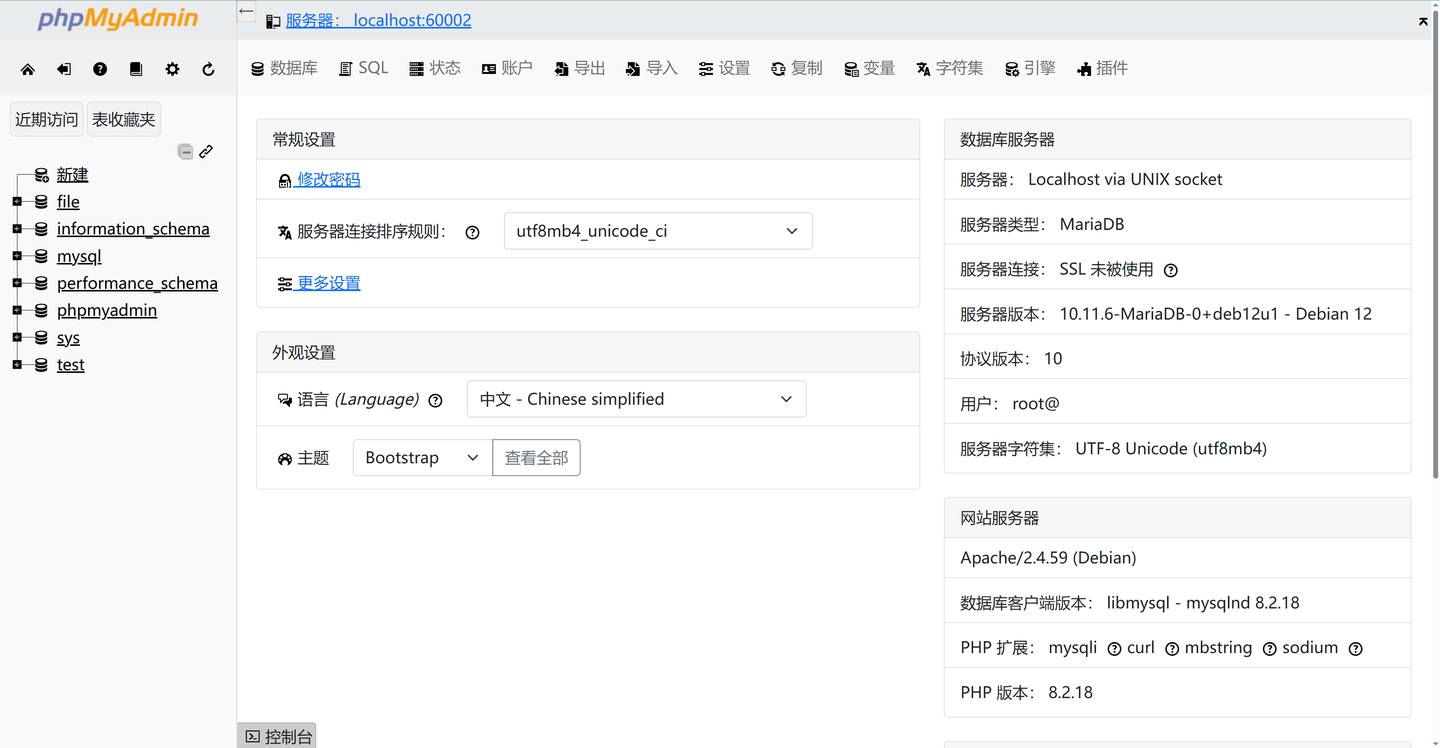
免费公益MYSQL(https://docs.ltpp.vip/LTPP-SHARE/mysql.html)
作为一名开发者或学生,数据库环境的搭建和维护往往是一个复杂且耗时的过程。但不用担心,现在有一款免费的MySQL服务器,专为解决您的烦恼而设计,让数据库的使用变得简单而高效。
性能卓越,满足需求
虽然它是免费的,但性能绝不打折。服务器提供了稳定且高效的数据库服务,能够满足大多数开发和学习场景的需求。
在线phpMyAdmin,管理更便捷
内置的在线phpMyAdmin管理面板,提供了一个直观且功能强大的用户界面,让您可以轻松地查看、编辑和管理数据库。
数据隐私提醒,安全第一
正如您所知,这是一项公共资源,因此我们强烈建议不要上传任何敏感或重要的数据。请将此服务器仅用于学习和实验目的,以确保您的数据安全。
免费在线WEB代码编辑器(https://docs.ltpp.vip/LTPP-WEB-IDE/)
无论你是开发者还是学生,编程环境的搭建和管理可能会占用你宝贵的时间和精力。现在,有一款强大的免费在线代码编辑器,支持多种编程语言,让您可以随时随地编写和运行代码,提升编程效率,专注于创意和开发。
多语言支持,无缝切换
这款在线代码编辑器支持包括C、C++、JavaScript、TypeScript、Go、Rust、PHP、Java、Ruby、Python3以及C#在内的多种编程语言,无论您的项目需要哪种语言,都能在这里找到支持。
在线运行,快速定位问题
您可以在编写代码的同时,即时运行并查看结果,快速定位并解决问题,提高开发效率。
代码高亮与智能提示
编辑器提供代码高亮和智能提示功能,帮助您更快地编写代码,减少错误,提升编码质量。
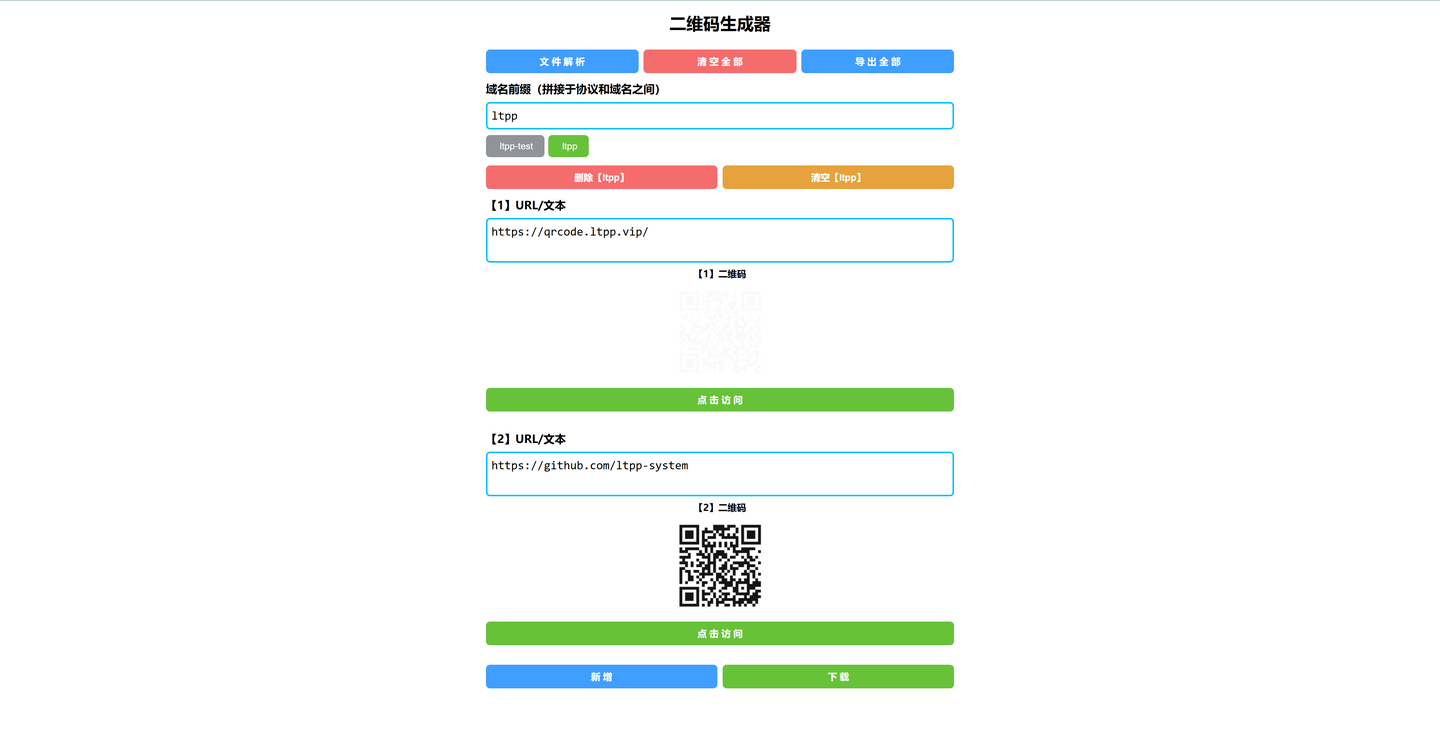
免费二维码生成器(https://docs.ltpp.vip/LTPP-QRCODE/)
二维码(QR Code)是一种二维条码,能够存储更多信息,并且可以通过智能手机等设备快速扫描识别。它广泛应用于各种场景,如:
企业宣传
企业可以通过二维码分享公司网站、产品信息、服务介绍等。
活动推广
活动组织者可以创建二维码,参与者扫描后可以直接访问活动详情、报名链接或获取电子门票。
个人信息分享
个人可以生成包含联系方式、社交媒体链接、个人简历等信息的二维码。
电子商务
商家使用二维码进行商品追踪、促销活动、在线支付等。
教育
教师可以创建二维码,学生扫描后可以直接访问学习资料或在线课程。
交通出行
二维码用于公共交通的票务系统,乘客扫描二维码即可进出站或支付车费。 功能强大的二维码生成器通常具备用户界面友好,操作简单,即使是初学者也能快速上手和生成的二维码可以在各种设备和操作系统上扫描识别的特点。
![[C++] 小游戏 征伐 SLG DNF 0.0.2 版本 zty出品](/images/no-images.jpg)






