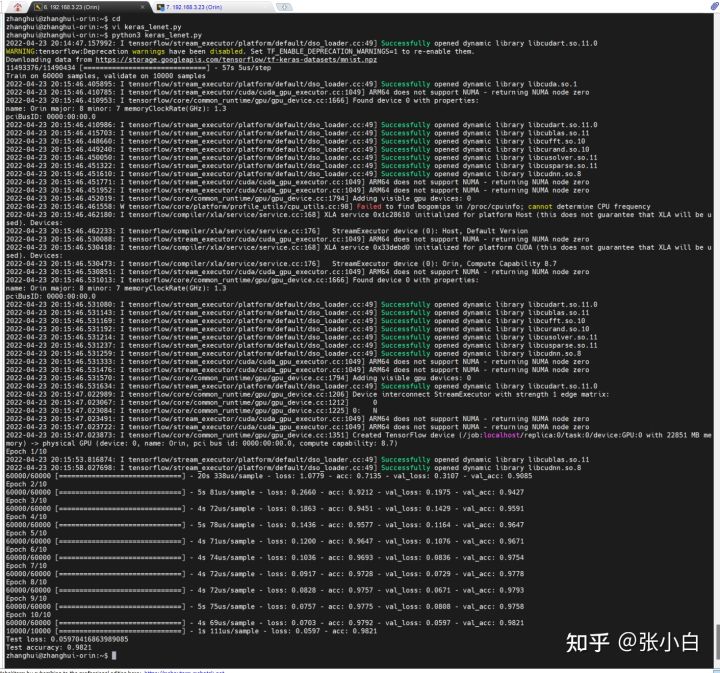
一、前言

Paper：Learning to Enhance Low-Light Image via Zero-Reference Deep Curve Estimation
Code：https://github.com/Li-Chongyi/Zero-DCE_extension

论文贡献：

首次提出不需要成对训练数据的低光增强网络，避免过拟合风险，在不同光照条件下泛化良好；
设计了一种逐像素高阶曲线，通过多次反复迭代可以有效地在宽动态范围中执行亮度映射；
展现了在缺少参考图像的情况下通过无参考损失函数训练图像增强网络的潜力；
所提出的Zero-DCE网络可以在减小计算量的同时保持增强能力，提供了多种选择以平衡增强能力和计算开销。

二、算法理解

2.1 低光增强曲线

受PS中亮度调整曲线的启发，作者尝试设计一种自动将低光图像映射到增强版本的曲线，并且自适应曲线的参数仅与输入的图像有关。既然是拟合曲线，自然而然就能想到使用拟合能力强大的神经网络来解决。作者认为这种曲线应该具备以下特性：

增强图像的每个像素值应落在[0,1]的归一化范围，以避免由溢出截断所导致的信息丢失；
曲线应该是单调的，以保持相邻像素的差异；
形式尽可能简单，在梯度反向传播的过程中可微；

基于以上三个特性，作者设计了如下的二次曲线：

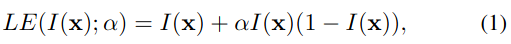
其中 $x$ 表示像素坐标， $\alpha \in[-1,1]$ 是可学习参数，同时控制曲线的级数和曝光水平。每个输入像素需要归一化到[0,1]，然后分别将曲线应用于RGB三个通道而不是只应用于亮度通道，这样做能保留固有的颜色并且能减小过饱和的风险。

对(1)式进行多次迭代能获取式(2)所示的高阶曲线，能够应对更具挑战性的低光场景， $n$ 为迭代次数，文中设为8.

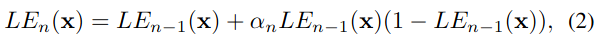
如果单张图像中所有像素都采用一条曲线，相当于全局映射，很容易造成局部过曝或欠曝。如果输入图像的每个像素都对应一条高阶曲线就能解决该问题，并且操作起来也比较简单，如式(3)所示，将系数 $\alpha$ 更改为与输入图像尺寸相同的系数矩阵 $\mathcal{A}$ 即可，因此每个像素都有一个对应的系数。

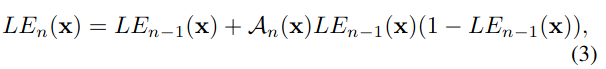
2.2 整体框架

整体框架比较简洁，输入一张RGB图像，经过DCE-Net输出 $3 * n = 3 * 8$ 共24张系数图（RGB共3个通道），然后将每个系数矩阵代入公式中迭代求解最终的增强图像。
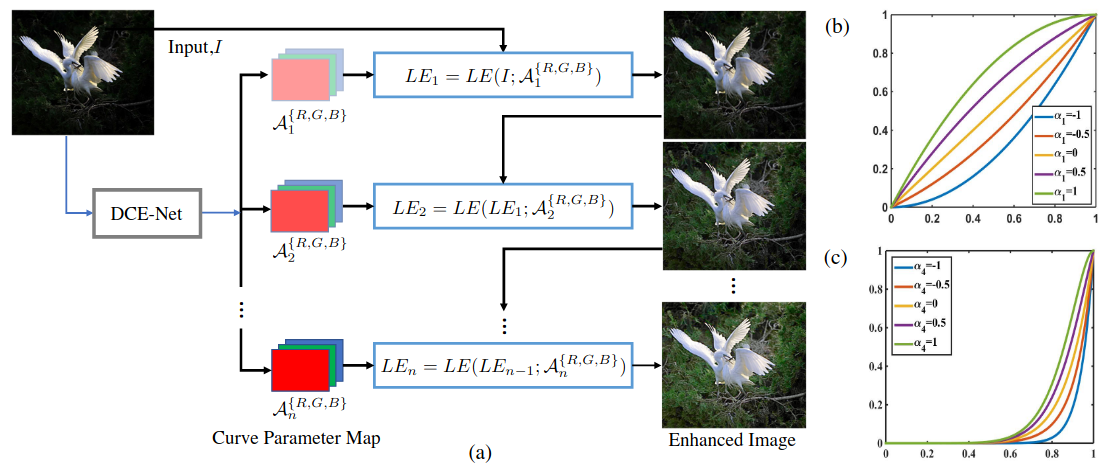
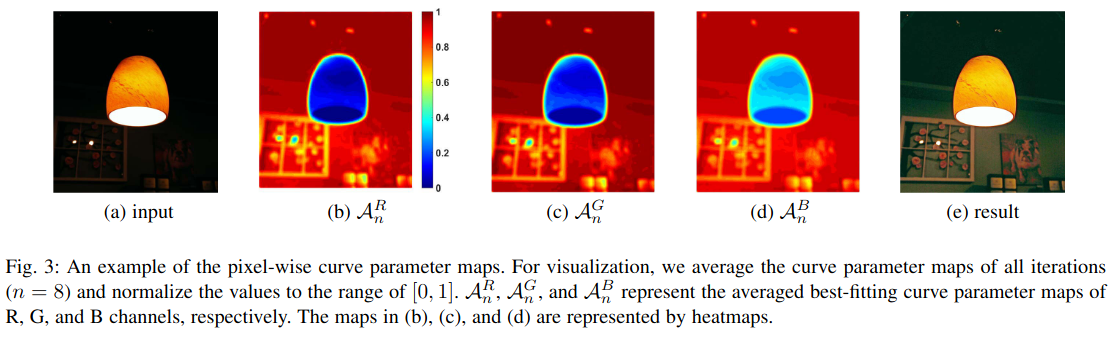
在这里插入图片描述
系数图 $\mathcal{A}$ 的一个示例，可以看到对于RGB任意通道，亮区的值都比较小，暗区的值较大。

2.3 网络结构

网络结构也很简洁，一共只有7个卷积层，加入了跳跃连接，注意最后一个卷积后面跟的是Tanh激活函数，保证输出的系数落入[-1,1]范围。因为迭代8次，RGB三个通道分别应用单独的曲线，所以输出通道为24。
在这里插入图片描述

2.4 损失函数

由于没有参考图像，因此作者从空间一致、曝光控制、色彩恒常、空间连续这四个角度出发，设计了由4个无参考损失函数所组成的总损失函数。

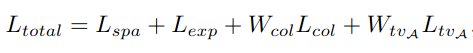
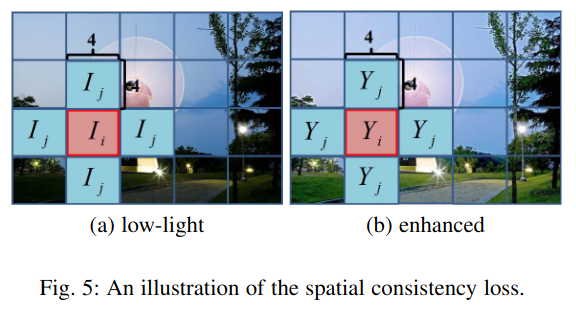
2.4.1 空间一致性

保持原始图像与增强图像相邻区域之间的差异尽可能接近，以确保增强后的图像与增强前在空间上是一致的。
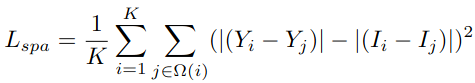
在这里插入图片描述
下图能够很清晰地解释空间一致性损失，将原始图像和增强后的图像划分为若干个大小为4x4的局部区域，对于每一个区域，计算其与上下左右4个邻域的差异，分别为 $I_i-I_j$ 和 $Y_i-Y_j$ ，再计算两者绝对值之差。（作者开源的代码中也写的很清晰，使用的是平均池化和卷积）

在这里插入图片描述

2.4.2 曝光控制

为了避免局部区域过曝或欠曝，将增强图像划分为 $M$ 个大小为16x16的局部区域，将每个局部区域的平均亮度 $Y$ 限制在 $E$ 附近，文中设置 $E = 0.6$
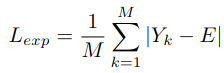
在这里插入图片描述

2.4.3 色彩恒常

根据灰度世界假设，对于一幅有着大量色彩变化的图像，其R,G,B 三个色彩分量的平均值趋于同一灰度值 K。对于增强图像，R、G、B三个通道的均值应该接近，基于此假设，作者设置了颜色恒常损失以保证增强图像的颜色正常。形式比较简单，3个通道两两之间分别求均值的MSE，再求和。
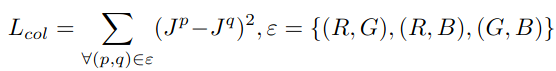
在这里插入图片描述

2.4.4 光照平滑

为了保持相邻像素间的单调性关系，在每个曲线参数图 $\mathcal{A}$ 上添加一个光照平滑损失，也就是常见的总变差损失，通过限制水平和垂直梯度来促使增强后的图像具有空间连续性。

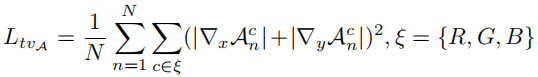
2.5 Zero-DCE++

虽然Zero-DCE的速度已经吊打各种暗光增强算法，但是作者通过调整网络结构提出了一个更轻量的版本Zero-DCE++，仅有10k参数，对于大小为1200×900×3图像，在单个GPU/CPU上的实时推理FPS能够达到1000/11。改进点如下：

将普通卷积替换为深度可分离卷积；
作者发现每个迭代阶段的曲线参数图 $\mathcal{A}$ 在大多数情况下是相似的，因此将参数图的数量由24减少到3，每次迭代复用3张参数图即可应对大多数场景（ $\mathcal{A}_n$ 变为 $\mathcal{A}$ ，每次迭代都使用 $\mathcal{A}$ ）；
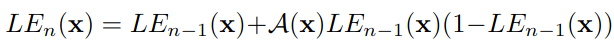
所提出的方法对输入图像的尺寸不敏感，因此可以将降采样后的图像作为网络输入，然后将输出的曲线参数图上采样回原始分辨率进行图像增强。