论文标题：FITS: Modeling Time Series with 10k Parameters

开源代码：https://anonymous.4open.science/r/FITS/README.md

前言

FITS（Frequency Interpolation Time Series Analysis Baseline）这篇文章发表于ICLR2024，也是之前SOTA的线性模型DLinear团队的最新论文。FITS的主要贡献在于基于傅立叶变换和低通滤波，通过在复频域内进行插值来操作时间序列，结合时域和频域优势，适用于边缘计算和实时分析任务，据作者所说，它具有大约10,000个参数。

我个人觉得，大家很要必要研读一下DLinear和FITS这两篇文章，不在于模型，而在于作者讲故事的能力和技巧。如何把一个结构简单的模型，放到一个特定的应用领域（边缘端）讲出来，特别是配合分析。

傅立叶变换

由于这篇文章的核心卖点之一就是进行了傅立叶变换，所以作者在论文中首先回顾了傅立叶变换的基本知识点，涉及时间序列数据从时域到频域的转换。

在傅里叶分析中，复频域是一种信号表示方法，其中每个频率分量都用一个复数来表征。这个复数包含了该频率分量的幅度和相位。频率分量的幅度代表了该分量在原始时域信号中的大小或强度。相对地，相位则表示了该分量引入的时间上的偏移或延迟。数学上，与频率分量相关联的复数可以表示为具有特定幅度和相位的复指数形式：

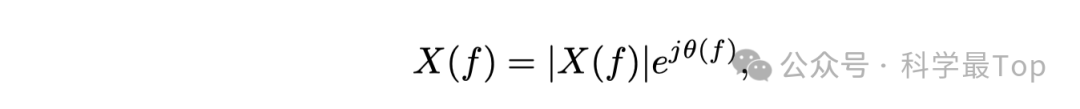
这里，𝑋(𝑓)是与频率分量 𝑓相关联的复数，∣𝑋(𝑓)∣ 是该分量的幅度，𝜃(𝑓) 是该分量的相位，而 𝑒^(𝑗𝜃(𝑓))是一个复指数，其中 𝑗 是虚数单位。如图 1(a) 所示，在复平面上，复指数元素可以被可视化为一个向量，其长度等于幅度 ∣𝑋(𝑓)∣，角度等于相位 𝜃(𝑓)。这个复指数同时包含了幅度和相位信息，使得我们能够全面地理解和分析信号的频率特性。

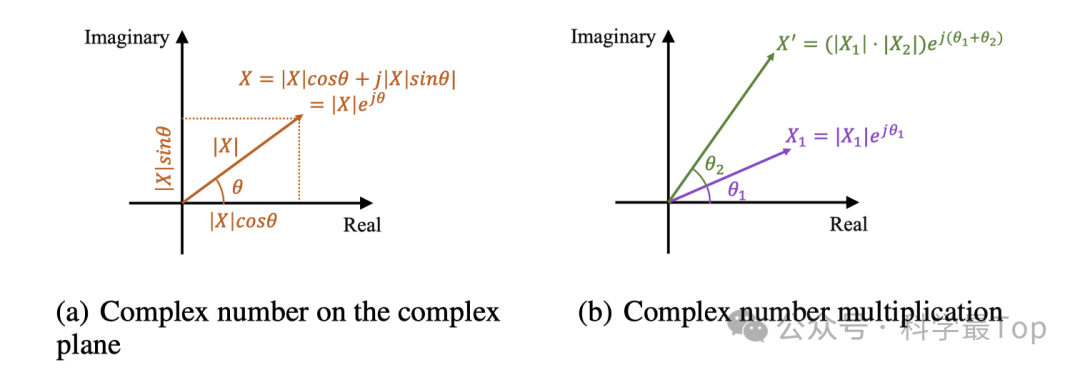
如果用三角函数表示，则如下公式，在这个表示中，cos⁡(𝜃(𝑓))和 sin⁡(𝜃(𝑓))分别是复数在复平面实轴和虚轴上的投影，而 𝑗是虚数单位。

𝑋(𝑓)=∣𝑋(𝑓)∣(cos⁡(𝜃(𝑓))+𝑗sin⁡(𝜃(𝑓)))

得到的复数特征由所有的频率分量组成，幅值最大的频率最能代表原始时域序列的周期。如果对该复数特征的每个频率分量进行复数域上的线性变换，使它和其他复数相乘，则会改变它的相位和幅值，如上图（b）。

FITS模型

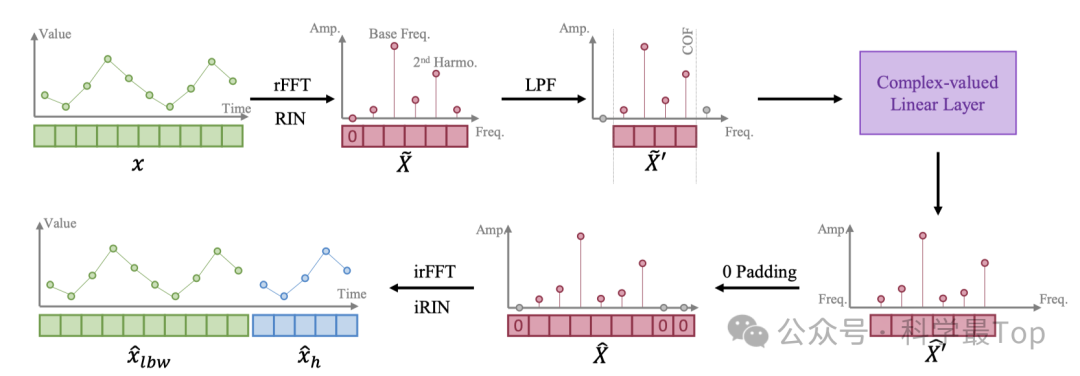
关于模型推荐大家结合代码来看，非常清晰，FITS的流程如图所示：

• 首先对于长度为L的序列，作者首先进行了RIN归一化，目的是为了使序列均值为0，然后使用傅立叶变换rFFT把时域信息转到频域（复数域）。

• 然后，使用低通滤波器（LPF）将高频分量过滤掉，这部分在代码中是通过一个cut_freq参数来确定的。这样的好处在于能够去掉噪声，减少模型参数量。

• 之后，通过图中紫色部分的Complex-valued Linear Layer，这部分是一个上采样（线性层），相当于对频率特征做了线性变换，其长度取决于pred_len和seq_len的比例。

• 最后，将新的频率特征进行零pad，使用傅立叶逆变换irFFT转回时域。

从上面的流程来看，整个FITS的核心就是三部分：傅立叶变换、复频率线性插值和低通滤波。我们着重看一下低通滤波，即到底应该过滤掉多少高频的频域信息。

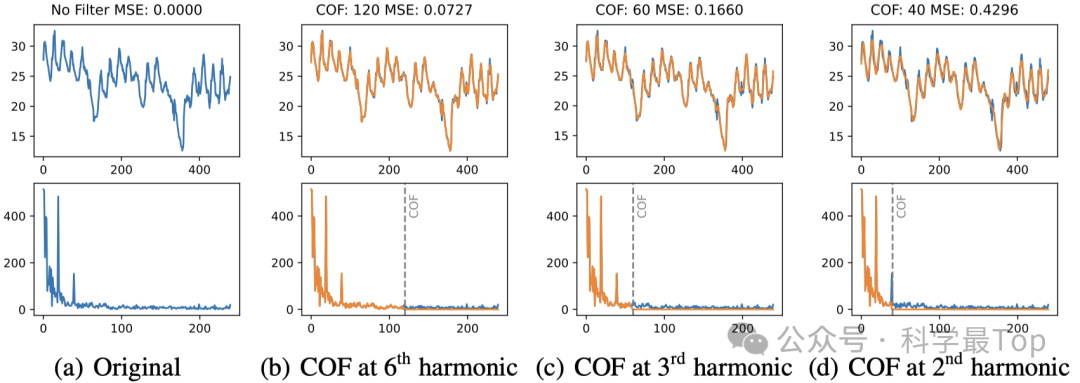
如图所示，即使只保留原始频域表示的四分之一，滤波后的波形也显示出最小的失真。此外，LPF滤除的高频分量通常包含噪声，这些噪声对于有效建模时间序列本质上是不相关的。

如果幅值最大频率为主频率，按照它的整数倍即harmonic分量来截断。

FITS对比试验

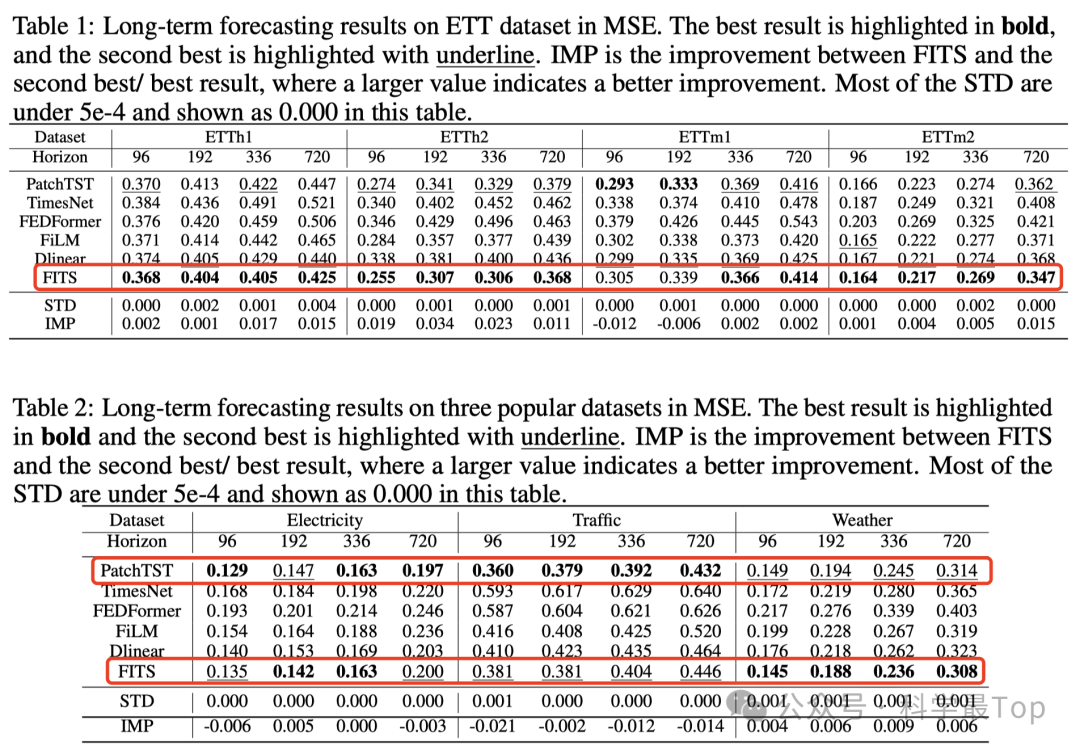
在模型参数量大大减少的情况下，FITS和Patch TST互有胜负，模型算是SOTA了。在比较推理速度，FITS的优势就出来了。

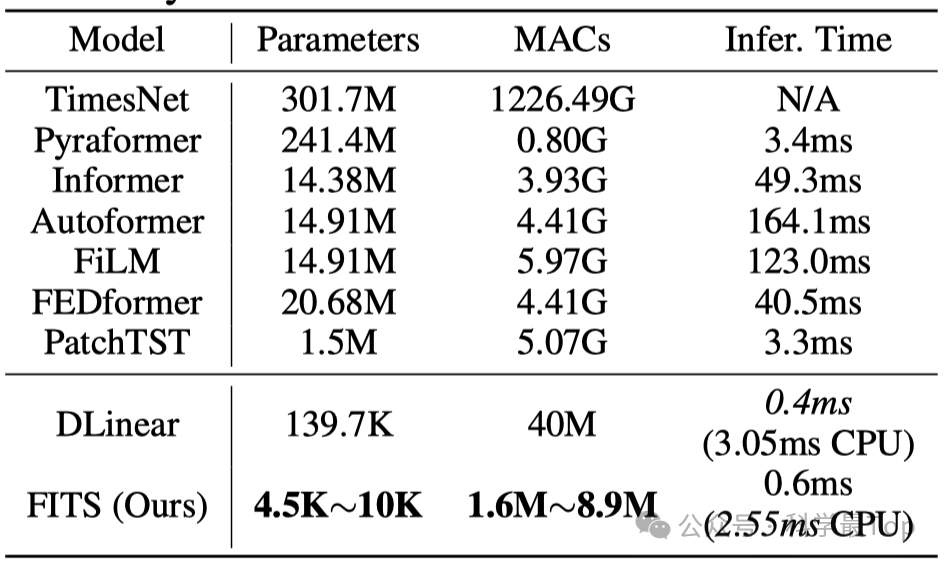
FITS总结

对于我们大多数普通团队来说，时间序列研究想从纯算法的角度SOTA好难😢。这篇文章换了一个赛道，在低参数量、快推理速度的边缘段，做了一个并不复杂的模型，发到了ICLR24，不得不佩服作者讲故事的能力和技巧。

---

大家一定要关注我的公众号【科学最top】，第一时间follow时序高水平论文解读！！！