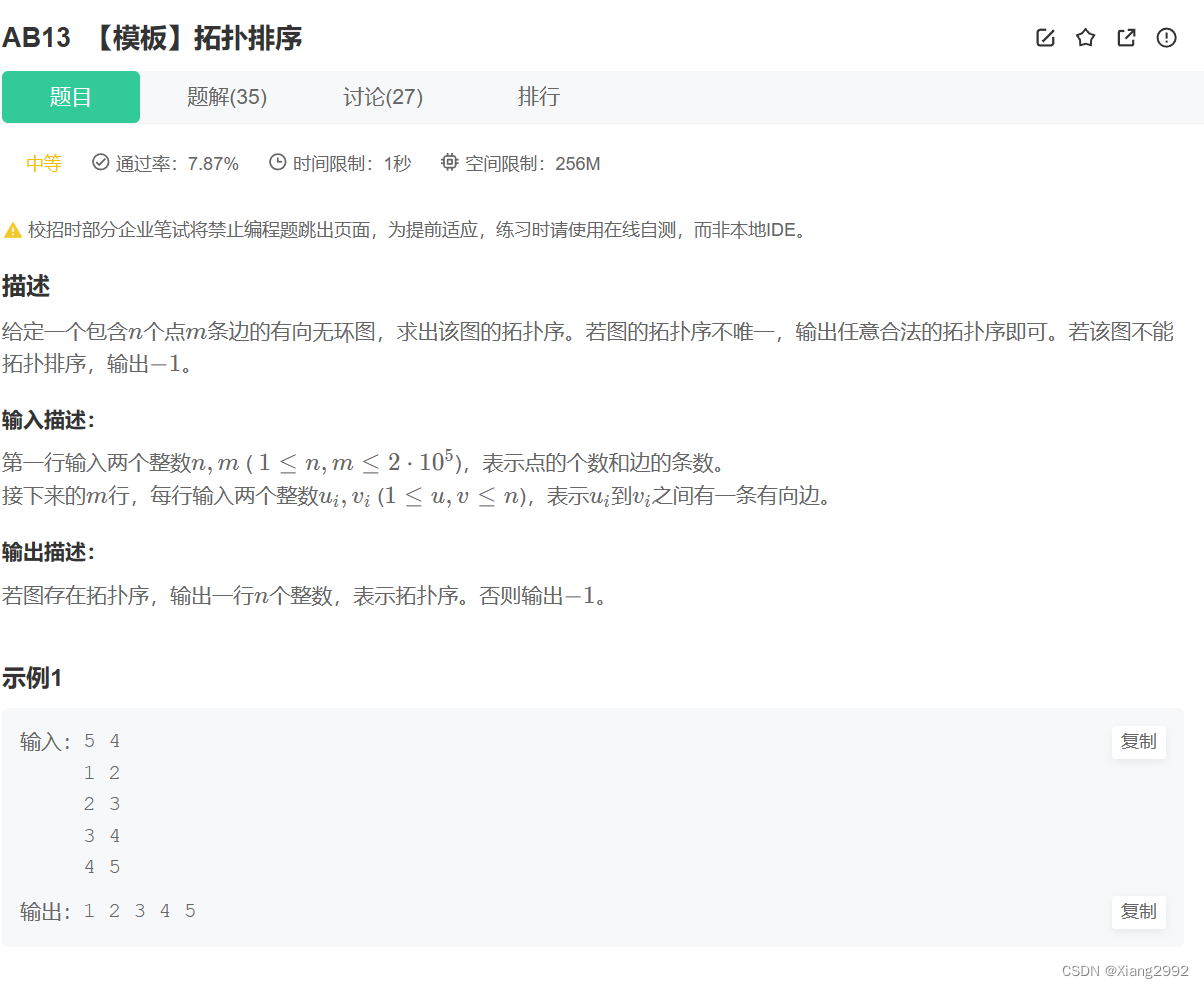
NO.1
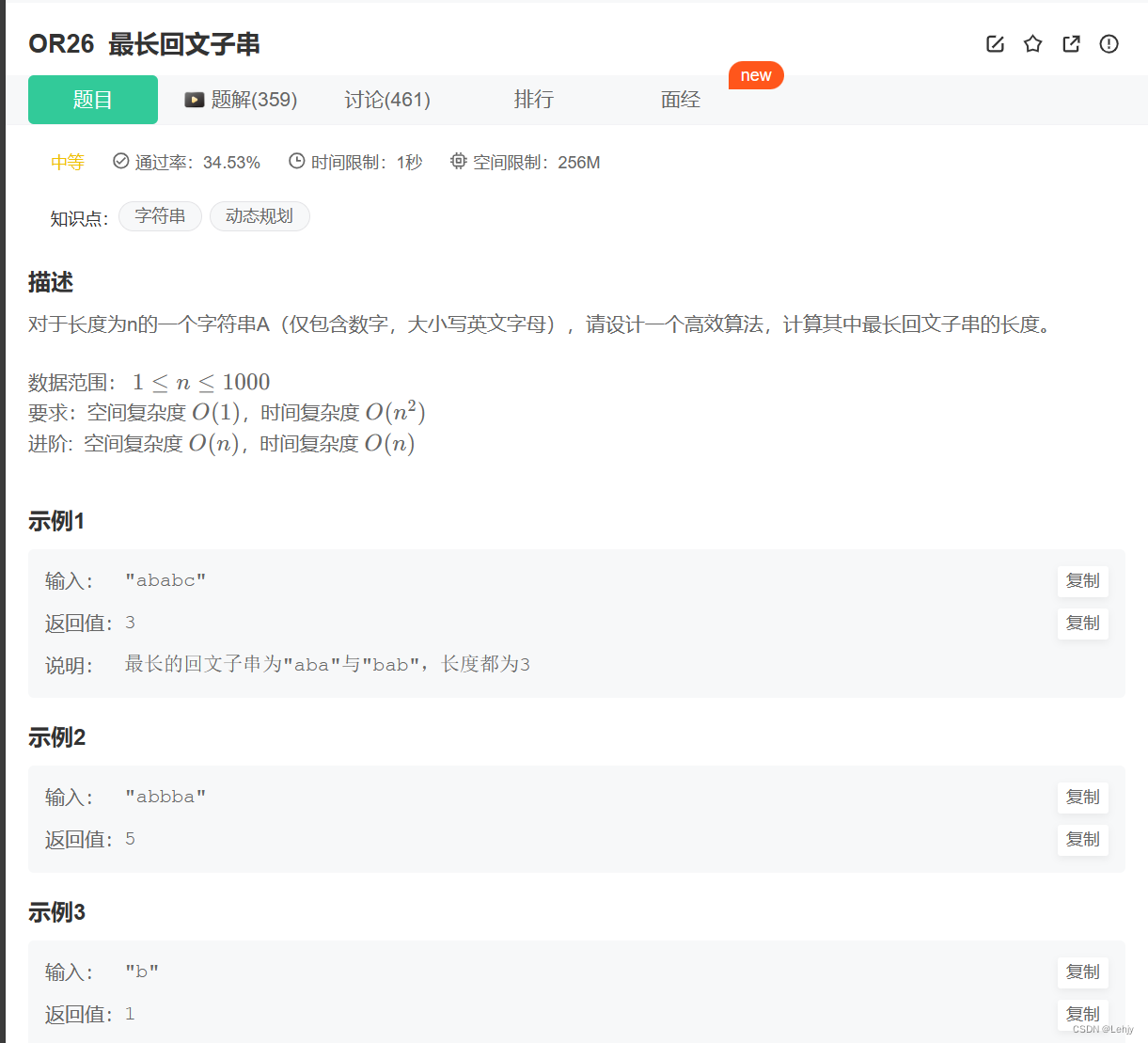
思路:中心扩展。从i位置开始,从i-1为左边和i+1右边进行移动,字符相等就继续移动,直到不等,更新回文串长度,让i为左边,i+1右边再移动,同样字符相等就移动,不等就更新长度。
代码实现:
class Solution {
public:int getLongestPalindrome(string A) {int n=A.size();int ret=0;for(int i=0;i<n;i++){int left=i-1,right=i+1;while(left>=0&&right<n&&A[left]==A[right]){left--;right++;}ret=max(ret,right-left-1);left=i,right=i+1;while(left>=0&&right<n&&A[left]==A[right]){left--;right++;}ret=max(ret,right-left-1);}return ret;}
};
NO.2
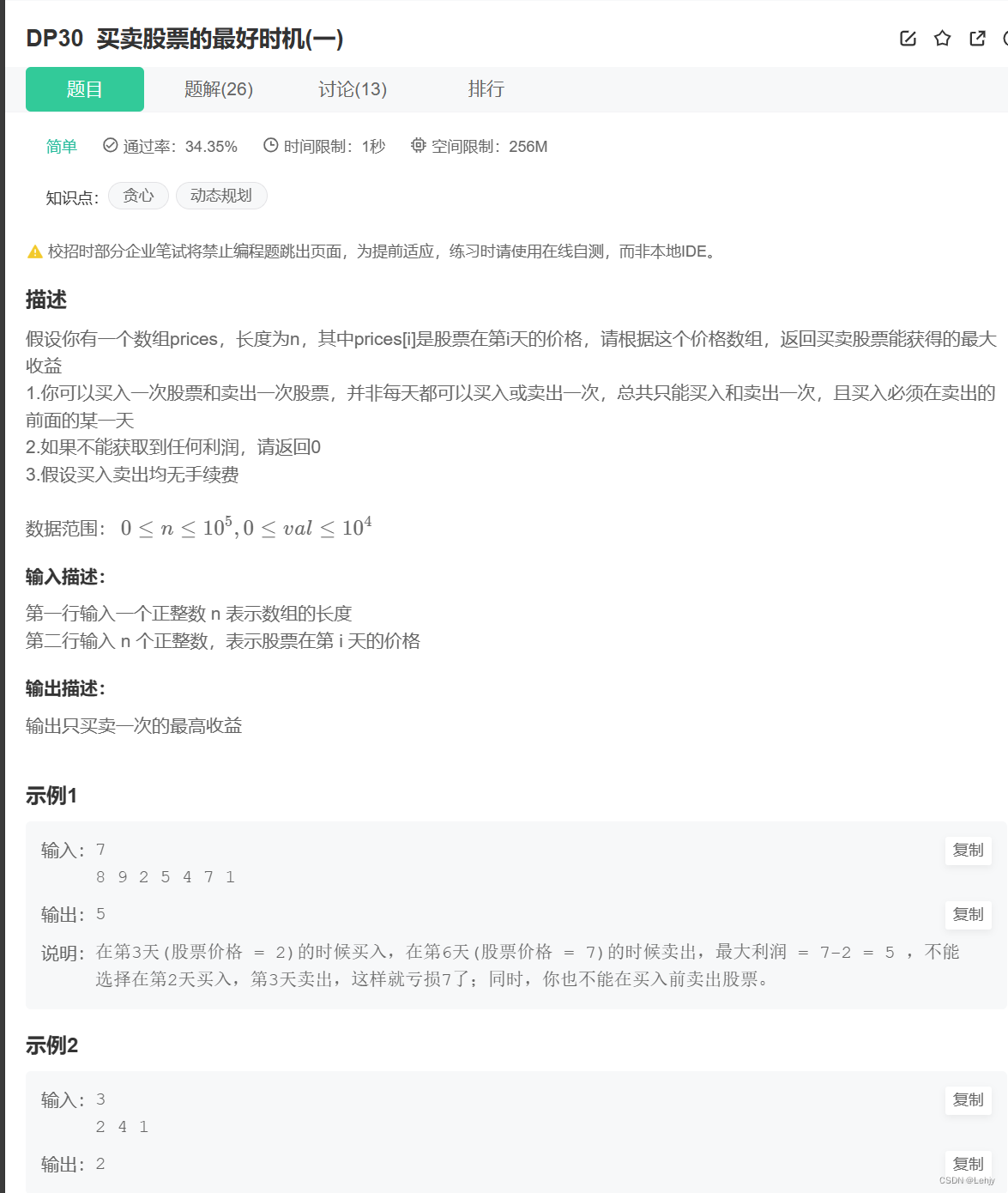
思路:定义一个前驱最小值,最大利润等于当前值减去前去最小值,前驱最小值等于当前值和它前驱最小值的最小值,利用一个循环遍历一遍就可以实现。
代码实现:
#include <iostream>
using namespace std;const int N=1e5+10;
int n;
int arr[N];int main() {cin>>n;for(int i=0;i<n;i++) cin>>arr[i];int ret=0,prevmin=arr[0];for(int i=1;i<n;i++){ret=max(ret,arr[i]-prevmin);prevmin=min(prevmin,arr[i]);}cout<<(ret<0?0:ret)<<endl;}
如果不想最后判断的话,最后调换一下ret和prevmin的最小值的顺序的就可以了。
#include <iostream>
using namespace std;const int N=1e5+10;
int n;
int arr[N];int main() {cin>>n;for(int i=0;i<n;i++) cin>>arr[i];int ret=0,prevmin=arr[0];for(int i=1;i<n;i++){prevmin=min(prevmin,arr[i]);ret=max(ret,arr[i]-prevmin);}cout<<ret<<endl;}
NO.3
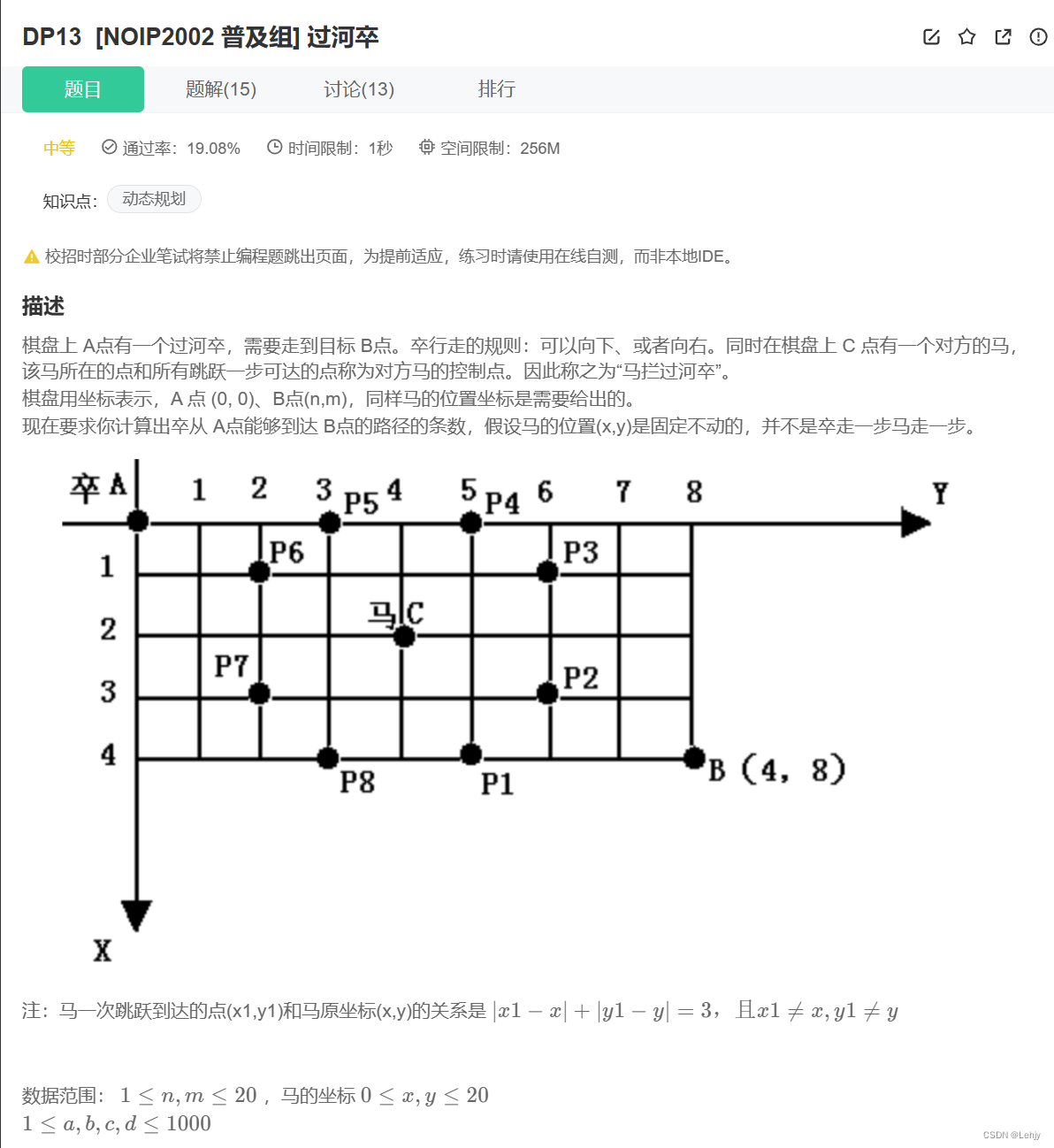
思路:dp路径问题,分情况讨论,如果要走的点为马控制的点或马本身的点,那么dp[i][j]为0,否则dp[i][j]=dp[i][j-1]+dp[i-1][j],因为我们多开辟一行一列,所以初始化初始化的时候先x+1,y+1,保证能够关系映射,并且令dp[0][1]或者是dp[1][0]为1。
#include <iostream>
using namespace std;int n,m,x,y;
long long dp[25][25];int main() {cin>>n>>m>>x>>y;x+=1;y+=1;dp[0][1]=1;for(int i=1;i<=n+1;i++){for(int j=1;j<=m+1;j++){if(i!=x&&j!=y&&abs(i-x)+abs(j-y)==3||(i==x&&j==y)){dp[i][j]=0;}else {dp[i][j]=dp[i][j-1]+dp[i-1][j];}}}cout<<dp[n+1][m+1]<<endl;return 0;
}