《离散数学》是计算机专业的一门十分重要的专业基础课。离散数学作为有力的数学工具对计算机的发展、计算机研究起着重大的作用。目前,计算机科学中普通采用离散数学中的一些基本概念、基本思想和基本方法。通过本课程的学习,掌握数理逻辑、集合论、代数和图论等近代数学分支的最基本知识:培养抽象思维能力及逻辑思维能力。
- (一) 命题逻辑的等值演算与推理演算
- 1.命题逻辑的基本概念、命题逻辑联结词与真值表,重言式
- 2.简单命题的形式化(简单自然语句的形式化)
- 3.等值定理、基本等值公式以及等值演算
- 4.命题公式与真值表的关系、联结词的完备集
- 5.析取范式、合取范式、主析取范式和主合取范式
- 6.命题逻辑的推理规则与推理演算,归结推理证明方法
- 7.命题逻辑公理系统的概念,公理系统的基本结构
- (二) 谓词逻辑的等值演算和推理演算
- 1.谓词、量词的基本概念及表示法
- 2.复杂自然语句的形式化
- 3.否定型等值式、量词分配等值式
- 4.范式、前束范式,Skolem 标准形
- 5.基本推理公式及其证明方法
- 6.谓词逻辑的推理规则与推理演算,归结推理法
- (三) 集合与关系
- 1.集合的概念、性质和基本运算,集合间的关系和特殊集合
- 2.有限集合的基数,包含排斥原理
- 3.集合论公理系统,无穷公理和自然数集合
- 4.二元关系的概念、关系矩阵和关系图
- 5.关系的逆、合成,关系的基本性质,关系的闭包
- 6.等价关系和划分,偏序关系与哈斯图
- 7.任意集合上的函数定义与性质、特殊函数,满射、单射与双射
- 8.集合的势、无限集合的基数
- (四) 图论的基本概念、路与回路
- 1.图的基本概念与性质
- 2.图的代数表示
- 3.途径、路、回路、迹的定义
- 4.欧拉环游(欧拉闭迹)与欧拉迹
- 5.汉密尔顿路与回路
- 6.最短路径
- 7.连通性
- 8.有向图
- (五) 树、平面图与图的着色
- 1.树的定义及等价条件
- 2.支撑树的计数
- 3.森林
- 4.最短树
- 5.平面图与极大平面图
- 6.对偶图
- 7.色数与色多项式
- (六) 代数结构
- 1.代数系统的概念
- 2.同构与同态
- 3.群的基本知识
- 4.循环群、群的同构
- 5.变换群和置换群、Caylay 定理
- 6.陪集和群的陪集分解、Lagrange 定理
- 7.正规子群与商群
- 8.同态、同态基本定理
- 9.环和域的概念
数理逻辑
数理逻辑是研究演绎推理的一门学科,用数学的方法来研究推理的规律统称为数理逻辑。
数理逻辑在问路问题中、排队论问题中的应用有很多。
命题逻辑
命题及其表示法
原子命题(简单命题): 不能再分解为更为简单命题的命题。例如:雪是黑色的。
复合命题: 由联结词、标点符号和原子命题复合而成的命题。例如:如果今天晚上有星星,那么明天就是睛天。
表示命题的符号称为命题标识符。
一个命题标识符如表示确定的命题,就称为命题常量。即命题常元有确定的真值。
如果命题标识符只表示任意命题的位置标志,就称为命题变元。即命题变元的真值待定。只有当用某具体命题带入命题变元后,它才有确定的真值。
当命题变元表示原子命题时,该变元称为原子变元。
例:
A A A:中国的首都在北京
B B B:上海是个美丽的城市
P P P:命题 X X X 和命题 Y Y Y。
其中: A A A 和 B B B 是命题常元, P P P 是命题变元。
命题联结词
在数理逻辑中,复合命题是由原子命题与逻辑联结词组合而成,联结词是复合命题中的重要组成部分。
命题联结词,两个句子真值之间的联结。
为了便于书写和进行推演,必须对联结词作出明确规定并符号化。
否定联结词: ¬ \neg ¬,非
合取联结词: ∧ \land ∧ 与、且
析取联结词: ∨ \lor ∨,或
条件联结词: → \to →,“若…则…”“如果…就."“只有…才…”
等价联结词(双条件联结词): ↔ \leftrightarrow ↔,当且仅当
合取析取老是混怎么办?并析交合,析取就是并集,合取就是交集。
不可兼析取 ∨ ‾ \overline{\lor} ∨ 排斥、异或
与非: ↑ \uparrow ↑
或非 ↓ \downarrow ↓
条件否定 ⟶ c \stackrel{c}{\longrightarrow} ⟶c
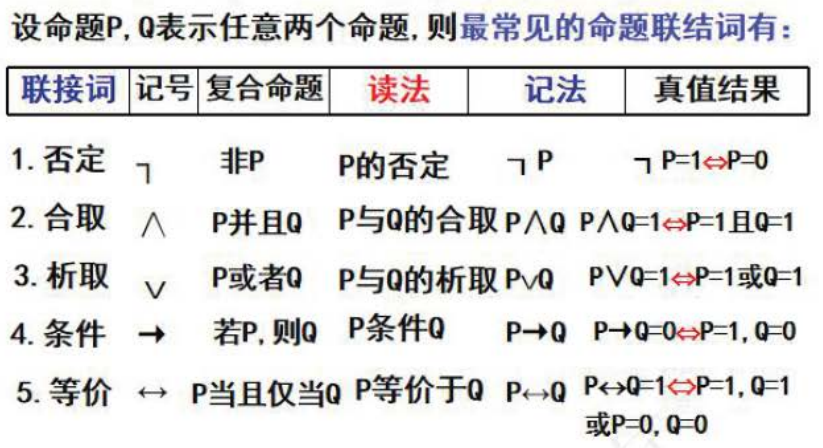
联结词说明
(1) 联结词是句子与句子之间的联结
(2) 联结词是两个句子真值之间的联结,而非句子的具体含义的联结,两个句子之间可以无任何地内在联系
(3) 联结词与自然语言之间的对应并非一一对应:
两个命题变元共能构成 16 16 16 种不等价的命题,而这些情况用 9 9 9 个联结词能够全部表示出来所以 9 9 9 个联结词就足够了
最小联结词组:必须是功能完备的,即任何命题公式都可以由最小联结词组中所包含的联结词来表示。对于最小联结词组,删除其中任何一个联结词就不能把所有的命题表达出来。
命题公式
设 P P P 和 Q Q Q 是任意两个命题,则 ¬ P \neg P ¬P, P ∨ Q P \lor Q P∨Q, ( P ∨ Q ) ∨ ( P → Q ) (P \lor Q) \lor (P \to Q) (P∨Q)∨(P→Q), P ↔ ( Q ∨ ¬ P ) P \leftrightarrow (Q \lor \neg P) P↔(Q∨¬P) 等都是复合命题。
若 P P P 和 Q Q Q 是命题变元,则上述各式均称作命题公式。 P P P 和 Q Q Q 称作命题公式的分量。
必须注意:命题公式是没有真假值的,仅当在一个公式中命题变元用确定的命题代人时,才得到一个命题。这个命题的真值,依赖于代换变元的那些命题的真值。此外,并不是由命题变元,联结词和一些括号组成的字符串都能成为命题公式。
命题公式(propositional formula) 亦称合式公式,是数理逻辑术语,它是按照一定规律形成的符号序列,在命题演算中,公式通常用归纳定义给出,例如,在一个具有五个联结词 ¬ , ∧ , ∨ , → , ↔ \neg,\land,\lor,\to,\leftrightarrow ¬,∧,∨,→,↔ 的系统中,合式公式定义如下:
(1) 单个命题变元本身是一个命题公式;
(2) 如果 A A A 是命题公式,则 ¬ α \neg α ¬α 是命题公式;
(3) 如果 A A A 和 B B B 是命题公式,则 A ∨ B A \lor B A∨B, A ∧ B A \land B A∧B, A → B A \to B A→B, A ↔ B A \leftrightarrow B A↔B 均为命题公式;
(4) 当且仅当有限次的应用 1~3 条所得到的包含命题变元,联结词和括号的符号串是命题公式。
因此,根据上述定义, ¬ p \neg p ¬p, ( p → q ) ∨ ¬ p (p \to q) \lor \neg p (p→q)∨¬p 等是公式,而 p ¬ p \neg p¬, p q → pq \to pq→等都不是公式。
有了联结词的合式公式概念,我们可以把自然语言中的有些语句,翻译成数理逻辑中的符号形式。
命题公式的真值表
设 P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P1,P2,⋯,Pn 是出现在公式 G G G 中的所有命题变元,指定 P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P1,P2,⋯,Pn 一组真值,则这组真值称为 G G G 的一个解释或指派,常记为 I I I。
一般来说,若有 n n n 个命题变元,则应有 2 n 2^n 2n 个不同的指派
将公式 G G G 在其所有可能指派下的真值情况列成表,称为 G G G 的真值表。
(1) 永真公式(重言式):给定一命题公式,若无论对分量作怎样的指派,其对应的真值永为 T T T,则称该命题公式为重言式或永真式。
(2) 永假公式(矛盾式)
(3) 蕴合式: 当且仅当 P → Q P \to Q P→Q 是一个重言式时,我们称“ P P P 蕴合 Q Q Q”,并记作 P ⇒ Q P \Rightarrow Q P⇒Q
重言式
定义: 重言式就是永真公式
定理: 任何两个重言式的合取或析取,仍然是一个重言式。
定理: 一个重言式,对同一分量用任何公式置换,其结果仍为重言式。
定理: 设 A A A, B B B 为两个命题公式, A ⇔ B A \Leftrightarrow B A⇔B 当且仅当 A ↔ B A \leftrightarrow B A↔B 为一重言式。
证明公式为重言式的方法:真值表法和等价公式推导。
例: P ∧ ( P → Q ) ⇒ Q P \land (P \to Q) \Rightarrow Q P∧(P→Q)⇒Q 为重言式
//TODO
蕴合式
若 P → Q P \to Q P→Q 是一个永真式,则称“ P P P 蕴含 Q Q Q”,记为 P ⇒ Q P \Rightarrow Q P⇒Q。
定理: 设 P P P、 Q Q Q 为任意两命题公式, P ⇔ Q P \Leftrightarrow Q P⇔Q 的充分必要条件是 P ⇒ Q P \Rightarrow Q P⇒Q 且 Q ⇒ P Q \Rightarrow P Q⇒P。
蕴合式性质: 设 A , B , C A,B,C A,B,C 为合式公式,若 A ⇒ B A \Rightarrow B A⇒B,且 A A A 为重言式,则 B B B 必是重言式;
蕴合式性质: 若 A ⇒ B A \Rightarrow B A⇒B, B ⇒ C B \Rightarrow C B⇒C 则 A ⇒ C A \Rightarrow C A⇒C。即蕴含关系是传递的。
蕴合式性质: 若 A ⇒ B A \Rightarrow B A⇒B 且 A ⇒ C A \Rightarrow C A⇒C,那么 A ⇒ ( B ∧ C ) A \Rightarrow (B \land C) A⇒(B∧C)。
蕴合式性质: 若 A ⇒ B A \Rightarrow B A⇒B 且 C ⇒ B C \Rightarrow B C⇒B,则 A ∨ C ⇒ B A \lor C \Rightarrow B A∨C⇒B
对 P → Q P \to Q P→Q 来说:
Q → P Q \to P Q→P 称作它的逆换式;
¬ P → ¬ Q \neg P \to \neg Q ¬P→¬Q 称作它的反换式;
¬ Q → ¬ P \neg Q \to \neg P ¬Q→¬P 称作它的逆反式;
有如下关系:
P → Q ⇔ ¬ Q → ¬ P P \to Q \Leftrightarrow \neg Q \to \neg P P→Q⇔¬Q→¬P
Q → P ⇔ ¬ P → ¬ Q Q \to P \Leftrightarrow \neg P \to \neg Q Q→P⇔¬P→¬Q
证明 A ⇒ B A \Rightarrow B A⇒B 的方法:
(1) 用 真值表法 、推导法 证明 A → B ⇔ T A \to B \Leftrightarrow T A→B⇔T (用定义)
(2) 用分析方法证明 A ⇒ B A \Rightarrow B A⇒B,有两种分析法
a. 假设前件 A A A 为真时推出后件 B B B 也为真,则 A ⇒ B A \Rightarrow B A⇒B;
b. 假设后件 B B B 为假时,推出前件 A A A 也为假,则 A ⇒ B A \Rightarrow B A⇒B;

例: P ∧ ( P → Q ) ⇒ Q P \land (P \to Q) \Rightarrow Q P∧(P→Q)⇒Q
//TODO
命题公式的等价公式
设 G G G、 H H H 是公式,如果在任意分量指派下, G G G 与 H H H 的真值相同,则称公式 G G G、 H H H 是等价的,记作 G ⇔ H G \Leftrightarrow H G⇔H。
例: 证明 ¬ P ∧ ¬ Q ⇔ ( P ∨ Q ) \neg P \land \neg Q \Leftrightarrow (P \lor Q) ¬P∧¬Q⇔(P∨Q)
证明两个公式等价的方法:真值表法和等价公式推导。

特别提示:必须牢记这 16 组等值式
命题公式的对偶式
在给定的命题公式 A A A 中,将联结词 ∨ \lor ∨ 换成 ∧ \land ∧, ∧ \land ∧ 换成 ∨ \lor ∨,若有特殊量 T T T 和 F F F,则 T T T 换为 F F F, F F F 换为 T T T,所得公式 A ∗ A^* A∗ 称为公式 A A A 的对偶式。
命题公式的范式
从真值表和对偶律等可以简化或推证一些命题公式。同一命题公式可以由各种相互等价的表达形式,为了把命题公式规范化,下面讨论命题公式的范式问题。
范式的概念
合取范式: 一个命题公式称为合取范式,当且仅当它具有型式: A 1 ∧ A 2 ∧ ⋯ ∧ A n ( n ≥ 1 ) A_1 \land A_2 \land \cdots \land A_n (n \ge 1) A1∧A2∧⋯∧An(n≥1),其中 A 1 , A 2 , ⋯ A n A_1,A_2,\cdots A_n A1,A2,⋯An 都是由命题变元或其否定所组成的析取式(注意这里)。
析取范式: 一个命题公式称为析取范式,当且仅当它具有型式: A 1 ∨ A 2 ∨ ⋯ ∨ A n ( n ≥ 1 ) A_1 \lor A_2 \lor \cdots \lor A_n (n \ge 1) A1∨A2∨⋯∨An(n≥1),其中 A 1 , A 2 , ⋯ A n A_1,A_2, \cdots An A1,A2,⋯An 都是由命题变元或其否定所组成的合取式(注意这里)。
注意:
(1) 析取范式、合取范式仅含联结词 { ¬ , ∧ , ∨ } \{\neg,\land,\lor\} {¬,∧,∨};
(2) 联结词 ¬ \neg ¬ 仅出现在命题变元前;
范式的求解方法
范式存在定理:对于任意命题公式,都存在与其等价的析取范式和合取范式。
求任意命题公式的合取范式或析取范式:
(1) 利用等价公式中的等价式和蕴涵式将公式中的 → \to →、 ↔ \leftrightarrow ↔ 用联结词 ¬ \neg ¬、 ∧ \land ∧ 和 ∨ \lor ∨ 来取代;
(2) 重复使用德·摩根定律将 ¬ \neg ¬ 移到各个命题变元的前端,并消去多余的 ¬ \neg ¬;
(3) 重复利用分配律、结合律,可将公式规约为合取范式(合取式的析取)或析取范式(析取式的合取);
注意:范式的不惟一性。
考虑公式:
( P ∨ Q ) ∧ ( P ∨ R ) (P \lor Q) \land (P \lor R) (P∨Q)∧(P∨R)
其与之等价的析取范式:
P ∨ ( Q ∧ R ) P \lor (Q \land R) P∨(Q∧R)
( P ∧ P ) ∨ ( Q ∧ R ) (P \land P) \lor (Q \land R) (P∧P)∨(Q∧R)
P ∨ ( Q ∨ Q ) ∨ ( Q ∧ R ) P \lor (Q \lor Q) \lor (Q \land R) P∨(Q∨Q)∨(Q∧R)
P ∨ ( P ∧ R ) ∨ ( Q ∧ R ) P \lor (P \land R) \lor (Q \land R) P∨(P∧R)∨(Q∧R)
由此产生了主析取范式和主合取范式的概念。
一个命题公式的主析取范式和主合取范式是唯一的。
主范式之小项和主析取范式
小项: n n n 个命题变元 P 1 P_1 P1、 P 2 P_2 P2、 P 3 P_3 P3、 ⋯ \cdots ⋯、 P n P_n Pn的合取式中,若每个命题变元与其否定不同时存在,但二者之一恰好出现一次且仅一次,则称此合取式为关于 P 1 、 P 2 、 P 3 、 ⋯ 、 P n P_1、P_2、P_3、\cdots、P_n P1、P2、P3、⋯、Pn 的一个小项。
越重合越小。
对于 n n n 个命题变元,可构成 2 n 2^n 2n 个小项。
例:
(1) 一个命题变元 P P P 对应的小项有两个: P P P、 ¬ P \neg P ¬P;
(2) 两个命题变元 P P P、 Q Q Q 对应的小项有四个:
P ∧ Q P \land Q P∧Q、 ¬ P ∧ Q \neg P \land Q ¬P∧Q、 P ∧ Q P \land Q P∧Q、 ¬ P ∧ ¬ Q \neg P \land \neg Q ¬P∧¬Q;
小项(整个合取式为小项)的性质:
没有两个小项等价;
每个小项当其真值指派与对应的编码相同时,真值为 1,其它情况均为 0;
任意两个不同小项的合取($ \land )为永假式 ∗ ∗ ;全体小项的 ∗ ∗ 析取( )为永假式**; 全体小项的**析取( )为永假式∗∗;全体小项的∗∗析取( \lor $)为永真公式;
主析取范式: 给定的析取范式中,每一个合取式都是小项,则称该范式为主析取范式。
对于一个命题公式的主析取范式,如将其命题变元的个数及出现次序固定后,则此公式的主析取范式便是唯一的,因此,给定任两个公式,由主析取范式可以方便地看出两个公式是否等价。
求主析取范式的方法:
(a) 真值表法
定理: 命题公式对应的真值表中真值结果为真的所有的行,找到其每一个分量指派所对应的小项将这些极小项进行析取即可得到相应的主析取范式。
例: 求公式 ( P → Q ) (P \to Q) (P→Q), ( P ∨ Q ) (P \lor Q) (P∨Q) 和 ¬ ( P ∧ Q ) \neg (P \land Q) ¬(P∧Q) 的主析取范式
第一步画图真值表

第二步找到每个公式所有真值为 T 的时候, P P P 和 Q Q Q 的指派。
比如命题公式 ( P → Q ) (P \to Q) (P→Q) 分别在 P = T & Q = T P=T \& Q=T P=T&Q=T, P = F & Q = T P=F \& Q = T P=F&Q=T 和 P = F & Q = F P=F \& Q=F P=F&Q=F 时为 T T T。
则 ( P → Q ) ⇔ ( P ∧ Q ) ∨ ( ¬ P ∧ Q ) ∨ ( ¬ P ∧ ¬ Q ) (P \to Q) \Leftrightarrow (P \land Q) \lor (\neg P \land Q) \lor (\neg P \land \neg Q) (P→Q)⇔(P∧Q)∨(¬P∧Q)∨(¬P∧¬Q)
例: 求公式 ( P → Q ) ↔ R (P \to Q) \leftrightarrow R (P→Q)↔R 的主析取范式
//TODO
(b) 等价公式推导法
(1) 先求出该公式所对应的析取范式;
(2) 去掉重复出现的命题变元、析取范式中的永假式;
(3) 若析取范式的某一个合取式缺少该命题公式中所规定的命题变元,则可用公式: ( P ∨ ¬ P ) ∧ Q ↔ Q (P \lor \neg P) \land Q \leftrightarrow Q (P∨¬P)∧Q↔Q 将命题变元 P P P 补进去,并利用分配律展开;
(4) 将相同的小项合并,同时利用交换律进行顺序调整,由此可转换成标准的主析取范式;
例: 求公式 ( P → Q ) ↔ R (P \to Q) \leftrightarrow R (P→Q)↔R 的主析取范式
//TODO
主范式之大项和主合取范式
大项: 在含有 n n n 个命题变元 P 1 、 P 2 、 P 3 、 ⋯ 、 P n P_1、P_2、P_3、\cdots、P_n P1、P2、P3、⋯、Pn 的析取式中,若每个命题变元与其否定不同时存在但二者之一恰好出现一次且仅一次,则称此析取式为关于 P 1 、 P 2 、 P 3 、 ⋯ 、 P n P_1、P_2、P_3、\cdots、P_n P1、P2、P3、⋯、Pn 的一个大项。
对于 n n n 个命题变元,可构成 2 n 2^n 2n 个大项。
越
例:
(1) 一个命题变元 P P P,对应的极大项有两项: P 、 ¬ P P、\neg P P、¬P;
(2) 两个命题变元 P 、 Q P、Q P、Q 对应的极大项有四项: P ∨ Q 、 ¬ P ∨ Q 、 P ∨ ¬ Q 、 ¬ P ∨ ¬ Q P \lor Q、\neg P \lor Q、P \lor \neg Q、\neg P \lor \neg Q P∨Q、¬P∨Q、P∨¬Q、¬P∨¬Q;
大项的性质:
(1) 没有两个大项等价;
(2) 每个大项当其真值指派与对应的编码相同时,真值为 0,其它情况均为 1;
(3) 任意两个不同大项的析取为永真式;
(4) 所有大项的合取为永假公式;
主合取范式: 给定的合取范式中,每一个析取式都是大项,则称该范式为主合取范式。
求主合取范式的方法:
(a) 真值表法
公式对应的真值表中真值结果为假的所有的行,找到其每一个解释所对应的大项,将这些大项进行合取即可得到相应的主合取范式。
例: 求公式 ( P → Q ) ↔ R (P \to Q) \leftrightarrow R (P→Q)↔R 的主合取范式
//TODO
(b) 等价公式推导法
(1) 先求出该公式所对应的合取范式;
(2) 去掉重复出现的命题变元、合取范式中的永真式;
(3) 若合取范式的某一个析取式缺少该命题公式中所规定的命题变元,则可用公式: ( P ∧ ¬ P ) ∨ Q ↔ Q (P \land \neg P) \lor Q \leftrightarrow Q (P∧¬P)∨Q↔Q 将命题变元 P P P 补进去,并利用分配律展开;
(4) 相同的小项合并,同时利用交换律进行顺序调整,由此可转换成标准的主合取范式;
例: 求公式 ( P → Q ) ↔ R (P \to Q) \leftrightarrow R (P→Q)↔R 的主合取范式
//TODO
主析取范式和主合取范式之间的转换

范式的作用
- 判断公式类型
- 判断公式是否等价
- 判断公式为真或为假的分量指派
命题演算中的推理规则
设 A , C A,C A,C 是两个命题公式。当且仅当 A → C A \to C A→C 为重言式,即 A ⇒ C A \Rightarrow C A⇒C,称 C C C 是 A A A 的有效结论,或 C C C 可由 A A A 逻辑推出。
推广:设 H 1 , ⋯ , H n , C H_1,\cdots,H_n,C H1,⋯,Hn,C 是命题公式。当且仅当公式 H 1 ∧ ⋯ ∧ H n ⇒ C H_1 \land \cdots \land H_n \Rightarrow C H1∧⋯∧Hn⇒C,称 C C C 是一组前提 H 1 , ⋯ , H n H_1,\cdots,H_n H1,⋯,Hn 的有效结论。
判别有效结论的过程就是论证过程,论证方法千变万化,但基本方法是真值表法、直接证法和间接证法。
判断有效结论的常用方法:
- 真值表法: 仅适用于命题变元少的情况。
- 直接证法:由一组前提,利用一些公认的推理规则,根据已知的等价或蕴含公式,推演得到有效的结论。P规则,T规则
- 间接证法: (1) 反证法(归缪法) (2) CP 规则
- 利用定义: A ⇒ B A \Rightarrow B A⇒B 当且仅当 A → B A \to B A→B 为重言式
谓词逻辑
命题逻辑能够解决的问题是有局限性的。只能进行命题间关系的推理,无法解决与命题的结构和成分有关的推理问题。
谓词逻辑这类推理中,各命题之间的逻辑关系不是体现在原子命题之间,而是体现在构成原子命题的内部成分之间。对此,命题逻辑将无能为力。
命题逻辑只考虑逻辑连接词的逻辑特性不考虑命题本身,谓词逻辑既考虑连接词的逻辑特性,还深入分析到命题内部考虑谓词及其量词的逻辑特性。
命题逻辑显然可以看作谓词逻辑的一个子集。 因为谓词逻辑中一般是允许出现 0 元谓词的。全部由 0 元谓词的构成的公式就是命题逻辑公式了。
当论域为一个大小确定的有限集时,一个谓词公式可以等价地转化成一个命题逻辑公式。
一阶谓词逻辑是命题逻辑的推广,二阶谓词逻辑是一阶谓词逻辑的推广。
谓词的概念与表示
命题是具有真假意义的陈述句,从语法上分析,一个陈述句由主语和谓语两部分组成。
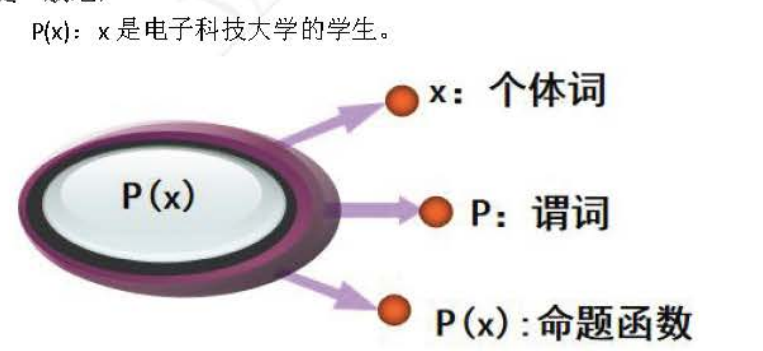
这个图很好的展示了,原子命题,个体词,谓词和命题函数之间的关系。
个体(客体): 不依赖于人的主观而客观存在的实体,可以是具体的物体,也可以是抽象概念。
个体常元: 具体的事务,用a,b,c表示
个体变元: 抽象的事物,用x,y,z表示
个体域(论域): 一个客体变元的取值范围;有限个体域,如 { a , b , c } , { 1 , 2 } \{a,b,c\},\{1,2\} {a,b,c},{1,2},无限个体域,如 N , Z , R , ⋯ N,Z,R,\cdots N,Z,R,⋯;全总个体域,由宇宙间一切事物组成。
谓词: 表示个体词性质或相互之间关系的词,一元谓词( n = 1 n=1 n=1)表示性质,如: F ( x ) F(x) F(x): x x x 具有性质 F F F;多元谓词( n ≥ 2 n \ge 2 n≥2)表示事物之间的关系,如 L ( x , y ) L(x,y) L(x,y): x x x 与 y y y 有关系 L L L。
一般用大写字母表示谓词,用小写字母表示客体名称。
用谓词表达命题,必须包括客体和谓词字母两个部分。
单独一个谓词不是完整命题,把谓词字母后填上客体所得的式子称为谓词填式。谓词和谓词填式是两个不同的概念。
一般地说, n n n 元谓词需要 n n n 个客体名称插入到固定地位置上,如果 A A A 为 n n n 元谓词, a 1 , a 2 , ⋯ , a n a_1,a_2,\cdots,a_n a1,a2,⋯,an 是客体的名称,则 A ( a 1 , a 2 , ⋯ , a n ) A(a_1,a_2,\cdots,a_n) A(a1,a2,⋯,an) 就可成为一个命题(一个谓词填式可以成为一个命题)。
单纯的谓词或单纯的个体词都无法构成一个完整的逻辑含义,只有将它们结合起来时才能构成一个独立的逻辑断言。
例: 他是三好学生,哥白尼指出地球绕着太阳转。
“是三好学生”,“指出”,是谓词,分别用大写字母 A A A 和 B B B 表示;
客体名称"他"和哥白尼和地球绕着太阳转分别用小写字母a,b,c表示。
则, A ( a ) A(a) A(a),B(b,c) 是谓词填式,这样的谓词填式可能是一个命题。
命题函数
由一个谓词,一些客体变元组成的表达式称为简单命题函数。
由一个或 n n n 个简单命题函数以及逻辑联结词组合而成的表达式称为复合命题函数。
例: L ( x , y ) L(x,y) L(x,y) 表示 x x x 小于 y y y,那么, L ( x , y ) L(x,y) L(x,y) 是一个命题函数而不是一个命题。当 x , y x,y x,y取定一个值时,如 L ( 2 , 3 ) L(2,3) L(2,3) 表示一个真命题, L ( 3 , 2 ) L(3,2) L(3,2) 表示一个假命题。
逻辑联结词在复合命题函数中与命题演算中的解释完全相同。
例: 设 S ( x ) S(x) S(x) 表示 x x x 学习好, W ( x ) W(x) W(x)表示 x x x 工作好,则 ¬ S ( x ) \neg S(x) ¬S(x) 表示 x x x 学习不好, ¬ W ( x ) \neg W(x) ¬W(x) 表示 x x x 工作不好,当 x x x 指人时是命题, x x x 指数时不是命题(不能确定真值)。
命题函数中客体变元的论域的量词
例: ( P ( X Y ) P ( Y Z ) ) P ( X , Z ) (P(XY) P(YZ)) P(X,Z) (P(XY)P(YZ))P(X,Z)
若 P ( x , y ) P(x,y) P(x,y) 解释为“ X X X 小于 Y Y Y”,当 X , Y , Z X,Y,Z X,Y,Z 都在实数域中取值时,为永真式。
若 P ( x , y ) P(x,y) P(x,y) 解释为“ X X X 为 Y Y Y 的儿子”,当 X , Y , Z X,Y,Z X,Y,Z 都指人为永假式。
若 P ( x , y ) P(x,y) P(x,y) 解释为“ X X X 距 Y 10 Y 10 Y10米”,当 X , Y , Z X,Y,Z X,Y,Z 表示地面上的房子,则该式可能为 T T T,也可能为 F F F,由 X , Y , Z X,Y,Z X,Y,Z 的具体位置而定。
命题函数确定为命题与客体变元的个体域有关。
**个体域:**在命题函数中,客体变元的论述范围称作个体域。
**全总个体域;**个体域可以是有限的,也可以是无限的,把各种个体域综合在一起作为论述范围的域称全总个体域。
全称量词: ( ∀ x ) (\forall x) (∀x),所有的 x x x;任意的 x x x;一切的 x x x;每一个 x x x;等等。
存在量词: ( ∃ x ) (\exist x) (∃x),有些 x x x;至少有一个 x x x;某一些 x x x;存在 x x x;等等。
谓词逻辑符号化的两条规则
注意:题目中没给个体域,一律用全总个体域
引入特性谓词 F ( x ) F(x) F(x): x x x 为人;
默认情况下,所有命题函数的个体域全部统一使用全总个体域,然后客体变元的变化范围用特性谓词(一元谓词表性质)加以限制。这种特性谓词在加入到命题函数中时必定遵循如下原则:
(1) 对于全称量词( ∀ \forall ∀),刻划其对应个体域范围的特性谓词作为蕴涵式之前件加入。
(2) 对于存在量词( ∃ x \exist x ∃x),刻划其对应个体域范围的特性谓词作为合取式之合取项加入。
例:
(1) 所有的人都要死。
(2) 有的人活到百岁以上。
现将这两个命题符号化,在符号之前必须明确个体域
第一种情况:考虑个体域 D D D 为人类集合。
(1) 命题符号化为 ∀ x F ( x ) \forall x F(x) ∀xF(x),其中 F ( x ) F(x) F(x): x x x 是要死的,命题为真。
(2) 命题符号化为 ∃ x G ( x ) \exist xG(x) ∃xG(x),其中 G ( x ) G(x) G(x): x x x 活到百岁以上,命题为真。
第二种情况:考虑个体 D D D 为全总个体域(所有个体域的综合)。则
(1) ∀ x F ( x ) \forall x F(x) ∀xF(x) 表示宇宙间一切事物都是要死的,这与原命题不符;
(2) ∃ x G ( x ) \exist xG(x) ∃xG(x) 表示在宇宙间一切事物中存在百岁以上的,不符合题意;
引进一个特性谓词 M ( X ) M(X) M(X): X X X 是人,有了特性谓词后,符号化为:
( ∀ x ) ( M ( x ) → F ( x ) ) (\forall x)(M(x) \to F(x)) (∀x)(M(x)→F(x))
( ∃ x ) ( M ( x ) ∧ G ( x ) ) (\exist x)(M(x) \land G(x)) (∃x)(M(x)∧G(x))
例: 在一阶逻辑中将下面命题符号化
(1) 人都爱美
(2) 有人用左手写字
个体域分别为
(a) D D D 为人类集合
(b) D D D 为全总个体域
解:
(a)
(1) ∀ x G ( x ) \forall xG(x) ∀xG(x), G ( x ) G(x) G(x): x x x 爱美
(2) ∃ x G ( x ) \exist xG(x) ∃xG(x), G ( x ) G(x) G(x): x x x 用左手写字
(b)
F ( x ) F(x) F(x): x x x 为人(特性谓词), G ( x ) G(x) G(x): x x x 爱美
(1) ∀ x ( F ( x ) → G ( x ) ) \forall x(F(x) \to G(x)) ∀x(F(x)→G(x))
(1) ∃ x ( F ( x ) ∧ G ( x ) ) \exist x (F(x) \land G(x)) ∃x(F(x)∧G(x))
谓词公式
原子谓词公式 = 命题变元 + 客体变元
谓词公式 = 原子谓词公式 x n + 逻辑联结词 + 量词;
谓词公式中的变元的约束
指导变元(作用变元)
作用域(辖域)
自由变元
n − k n-k n−k 元谓词
约束变元的换名
自由变元的代入
给定 α \alpha α 为一个谓词公式,其中有一部分公式形式为 ( ∀ x ) P ( x ) (\forall x)P(x) (∀x)P(x) 或 ( ∃ x ) P ( x ) (\exist x) P(x) (∃x)P(x)。这里 ∀ \forall ∀, ∃ \exist ∃ 后面所跟的 x x x 叫做量词的指导变元或作用变元( ∀ x V ( x ) \forall x V(x) ∀xV(x) 中的第一个 x x x 是指导变元或作用变元), P ( x ) P(x) P(x) 叫做相应量词的作用域或辖。在作用域中 x x x 的一切出现,称为 x x x 在 α \alpha α 中的约束出现。 x x x 亦称为被相应量词中的指导变元所约束。在 α \alpha α 中除去约束变元以外所出现的变元称作自由变元。自由变元是不受约束的变元,虽然它有时也在量词的作用域中出现(比如 ( ∀ x ) P ( x , y ) (\forall x) P(x,y) (∀x)P(x,y) 中的 y y y),但它不受相应量词中指导变元的约束,故我们可把自由变元看作是公式中的参数。
从约束变元的概念可以看出, P ( x 1 , x 2 , ⋯ , x n ) P(x_1,x_2,\cdots,x_n) P(x1,x2,⋯,xn) 是 n n n 元谓词,它有 n n n 个相互独立的自由变元,若对其中 k k k 个变元进行约束,则成为 n − k n-k n−k 元谓词,因此,谓词公式中如果没有自由变元出现,则该式就成为一个命题。例如, ( ∀ x ) P ( x , y , z ) (\forall x)P(x,y,z) (∀x)P(x,y,z) 是二元谓词。 ( ∃ y ) ( ∀ x ) P ( x , y , z ) (\exist y)(\forall x) P(x,y,z) (∃y)(∀x)P(x,y,z) 是一元谓词。
为了避免由于变元的约束与自由同时出现,引起概念上的混乱,故可对约束变元进行换名。使得一个变元在一个公式中只呈一种形式出现,即呈自由出现或呈约束出现。
采用如下二规则:
约束变元的换名
对公式 α \alpha α 中的约束变元更改名称符号,这种遵守一定规则的更改,称为约束变元的换名。其规则为:
(1) 对于约束变元可以换名,其更改的变元名称范围是量词中的指导变元,以及该量词作用域中所出现的该变元,在公式的其余部分不变。
(2) 换名时一定要更改为作用域中没有出现的变元名称。
将量词辖域中出现的某约束出现的个体变项及对应的指导变项改成另一个在辖域中未曾出现的个体变项,其余不变。
自由变元的代入
对于公式中的自由变元,也允许更改,这种更改叫做代入。自由变元的代入,亦需遵守一定的规则,这个规则叫做自由变元的代人规则,现说明如下:
(1) 对于谓词公式中的自由变元,可以作代入,代入时需对公式中出现该自由变元的每一处进行。
(2) 用以代入的变元与原公式中所有变元的名称不能相同。
将某自由变项用与公式中所有个体变项不同的变项符号代替且处处代替。如果谓词公式(例如 F ( x ) F(x) F(x))前,没有全称量词或者存在量词的约束,可以把 x x x 换成另一个字母,和其他谓词公式中的 x x x 区分开。
谓词公式的等价关系和蕴含关系
[定义] 若两个谓词公式 A A A 和 B B B 有共同的论域 E E E,且在任何解释下 A A A 与 B B B 有相同的真值,则称谓词公式 A A A 与 B B B 在 E E E 上等价,记作作 A ⇔ B A \Leftrightarrow B A⇔B 或 A ≡ B A \equiv B A≡B。
谓词公式是永真的;
谓词公式是不可满足的;
谓词公式是可满足的;
[定义] 若两个谓词公式 A A A 和 B B B 有相同的论域,且在任何解释下 A → B A \to B A→B 为 1 1 1,则称谓词公式 A A A 蕴含 B B B,记作 A ⇒ B A \Rightarrow B A⇒B。
量词转化律
¬ ∀ x A ( x ) ⇔ ∃ x ¬ A ( x ) ¬ ∃ x A ( x ) ⇔ ∀ x ¬ A ( x ) \begin{align*} \neg \forall x A(x) \Leftrightarrow \exist x \neg A(x) \\ \neg \exist x A(x) \Leftrightarrow \forall x \neg A(x) \end{align*} ¬∀xA(x)⇔∃x¬A(x)¬∃xA(x)⇔∀x¬A(x)
(1) 不是对于所有的 x x x 都 A ( x ) A(x) A(x) 等价于存在 x x x 不 A ( x ) A(x) A(x);
(2) 不存在 x x x A ( x ) A(x) A(x) 等价于对于所有的 x x x 不 A ( x ) A(x) A(x);
(3) 出现在量词之前的否定,不是否定该量词,而是否定被量化了的整个命题。
量词辖域扩张及收缩律
设命题 P P P 中不出现约束变元 x x x,则有:
∀ x A ( x ) ∨ P ⇔ ∀ x ( A ( x ) ∨ P ) ∀ x A ( x ) ∧ P ⇔ ∀ x ( A ( x ) ∧ P ) ∃ x A ( x ) ∨ P ⇔ ∃ x ( A ( x ) ∨ P ) ∃ x A ( x ) ∧ P ⇔ ∃ x ( A ( x ) ∧ P ) \begin{align*} \forall x A(x) \lor P \Leftrightarrow \forall x (A(x) \lor P) \\ \forall x A(x) \land P \Leftrightarrow \forall x (A(x) \land P) \\ \exist x A(x) \lor P \Leftrightarrow \exist x (A(x) \lor P) \\ \exist x A(x) \land P \Leftrightarrow \exist x (A(x) \land P) \end{align*} ∀xA(x)∨P⇔∀x(A(x)∨P)∀xA(x)∧P⇔∀x(A(x)∧P)∃xA(x)∨P⇔∃x(A(x)∨P)∃xA(x)∧P⇔∃x(A(x)∧P)
当谓词的变元与量词的指导变元不相同时,亦能有上述类似的公式(将上式中的 P P P 变为 P ( y ) P(y) P(y))。
量词分配律(★★★★★)
量词对各个联结词的分配律。
对任意谓词公式 A ( x ) A(x) A(x) 和 B ( x ) B(x) B(x) 有:
逻辑等价:
( ∀ x ) ( A ( x ) ∧ B ( x ) ) ⇔ ( ∀ x ) A ( x ) ∧ ( ∀ x ) B ( x ) ( ∃ x ) ( A ( x ) ∨ B ( x ) ) ⇔ ( ∃ x ) A ( x ) ∨ ( ∃ x ) B ( x ) (\forall x)(A(x) \land B(x)) \Leftrightarrow (\forall x)A(x) \land (\forall x)B(x) \\ (\exists{x})(A(x)∨B(x)) \Leftrightarrow (\exists{x})A(x)∨(\exists{x})B(x)\\ (∀x)(A(x)∧B(x))⇔(∀x)A(x)∧(∀x)B(x)(∃x)(A(x)∨B(x))⇔(∃x)A(x)∨(∃x)B(x)
逻辑蕴含:
设 P P P, Q Q Q 是谓词公式,若 P → Q P \to Q P→Q 为永真式,则 P P P 永真蕴含 Q Q Q,记为 P ⇒ Q P \Rightarrow Q P⇒Q。
( ∀ x ) A ( x ) ∨ ( ∀ x ) B ( x ) ⇒ ( ∀ x ) ( A ( x ) ∨ B ( x ) ) ( ∃ x ) ( A ( x ) ∧ B ( x ) ) ⇒ ( ∃ x ) A ( x ) ∧ ( ∃ x ) B ( x ) ∃ x ( A ( x ) → B ( x ) ) ⇒ ∀ x A ( x ) → ∃ x B ( x ) (\forall x)A(x) \lor (\forall x)B(x) \Rightarrow (\forall x)(A(x) \lor B(x)) \\ (\exists{x})(A(x) \land B(x)) \Rightarrow (\exists{x})A(x) \land (\exists{x})B(x) \\ \exist x(A(x) \to B(x)) \Rightarrow \forall x A(x) \to \exist x B(x) (∀x)A(x)∨(∀x)B(x)⇒(∀x)(A(x)∨B(x))(∃x)(A(x)∧B(x))⇒(∃x)A(x)∧(∃x)B(x)∃x(A(x)→B(x))⇒∀xA(x)→∃xB(x)
多个量词的使用
( ∀ x ) ( ∀ y ) A ( x , y ) ⇔ ( ∀ y ) ( ∀ x ) A ( x , y ) ( ∃ x ) ( ∃ y ) A ( x , y ) ⇔ ( ∃ y ) ( ∃ x ) A ( x , y ) \begin{align*} (\forall x)(\forall y)A(x,y) \Leftrightarrow (\forall y)(\forall x)A(x,y) \\ (\exist x)(\exist y)A(x,y) \Leftrightarrow (\exist y)(\exist x)A(x,y) \end{align*} (∀x)(∀y)A(x,y)⇔(∀y)(∀x)A(x,y)(∃x)(∃y)A(x,y)⇔(∃y)(∃x)A(x,y)
( ∀ x ) ( ∀ y ) A ( x , y ) ⇒ ( ∃ y ) ( ∀ x ) A ( x , y ) ( ∀ y ) ( ∀ x ) A ( x , y ) ⇒ ( ∃ x ) ( ∀ y ) A ( x , y ) ( ∀ x ) ( ∃ y ) A ( x , y ) ⇒ ( ∃ y ) ( ∃ x ) A ( x , y ) ( ∀ y ) ( ∃ x ) A ( x , y ) ⇒ ( ∃ x ) ( ∃ y ) A ( x , y ) ( ∃ y ) ( ∀ x ) A ( x , y ) ⇒ ( ∀ x ) ( ∃ y ) A ( x , y ) ( ∃ x ) ( ∀ y ) A ( x , y ) ⇒ ( ∀ y ) ( ∃ x ) A ( x , y ) \begin{align*} (\forall x)(\forall y)A(x,y) \Rightarrow (\exist y)(\forall x)A(x,y) \\ (\forall y)(\forall x)A(x,y) \Rightarrow (\exist x)(\forall y)A(x,y) \\ (\forall x)(\exist y)A(x,y) \Rightarrow (\exist y)(\exist x)A(x,y) \\ (\forall y)(\exist x)A(x,y) \Rightarrow (\exist x)(\exist y)A(x,y) \\ (\exist y)(\forall x)A(x,y) \Rightarrow (\forall x)(\exist y)A(x,y) \\ (\exist x)(\forall y)A(x,y) \Rightarrow (\forall y)(\exist x)A(x,y) \end{align*} (∀x)(∀y)A(x,y)⇒(∃y)(∀x)A(x,y)(∀y)(∀x)A(x,y)⇒(∃x)(∀y)A(x,y)(∀x)(∃y)A(x,y)⇒(∃y)(∃x)A(x,y)(∀y)(∃x)A(x,y)⇒(∃x)(∃y)A(x,y)(∃y)(∀x)A(x,y)⇒(∀x)(∃y)A(x,y)(∃x)(∀y)A(x,y)⇒(∀y)(∃x)A(x,y)
一句话总结:前四个是大范围推小范围。全称量词和存在量词在公式中出现的次序,不能随意更换,后不同约束变元的存在(存在量词)和所有(全称量词)可以交换。
例: 利用谓词之间的等价关系证明下列公式之间的关系: ( ∀ x ) P ( x ) → Q ( x ) ⇔ ( ∃ y ) ( P ( y ) → Q ( x ) ) (\forall x) P(x) \to Q(x) \Leftrightarrow (\exist y)(P(y) \to Q(x)) (∀x)P(x)→Q(x)⇔(∃y)(P(y)→Q(x))
( ∀ x ) P ( x ) → Q ( x ) ⇔ ¬ ( ∀ x ) P ( x ) ∨ Q ( x ) ⇔ ( ∃ x ) ¬ P ( x ) ∨ Q ( x ) ⇔ ( ∃ y ) ¬ P ( y ) ∨ Q ( x ) ⇔ ( ∃ y ) ( ¬ P ( y ) ∨ Q ( x ) ) ⇔ ( ∃ y ) ( P ( y ) → Q ( x ) ) \begin{align*} &(\forall x)P(x) \to Q(x) \\ \Leftrightarrow &\neg (\forall x) P(x) \lor Q(x) \tag{蕴含等值式} \\ \Leftrightarrow &(\exist x) \neg P(x) \lor Q(x) \tag{量词否定律} \\ \Leftrightarrow &(\exist y) \neg P(y) \lor Q(x) \tag{换名规则} \\ \Leftrightarrow &(\exist y) (\neg P(y) \lor Q(x)) \tag{量词辖域扩张及收缩律} \\ \Leftrightarrow &(\exist y) (P(y) \to Q(x)) \tag{???} \end{align*} ⇔⇔⇔⇔⇔(∀x)P(x)→Q(x)¬(∀x)P(x)∨Q(x)(∃x)¬P(x)∨Q(x)(∃y)¬P(y)∨Q(x)(∃y)(¬P(y)∨Q(x))(∃y)(P(y)→Q(x))(蕴含等值式)(量词否定律)(换名规则)(量词辖域扩张及收缩律)(???)
谓词公式的标准型——前束范式
如果公式中的一切量词都位于该公式的最前端(不含否定词)且这些量词的辖域都延伸到公式的末端,称公式是一个前束范式。
例: 求下列公式的前束范式
(1) ¬ ∃ x ( M ( x ) ∧ F ( x ) ) \neg \exist x (M(x) \land F(x)) ¬∃x(M(x)∧F(x))
解:
¬ ∃ x ( M ( x ) ∧ F ( x ) ) ⇔ ∀ x ( ¬ M ( x ) ∨ ¬ F ( x ) ) ⇔ ∀ x ( M ( x ) → ¬ F ( x ) ) \begin{align*} &\neg \exist x (M(x) \land F(x)) \\ \Leftrightarrow &\forall x (\neg M(x) \lor \neg F(x)) \tag{量词否定等值式}\\ \Leftrightarrow &\forall x (M(x) \to \neg F(x)) \tag{???} \end{align*} ⇔⇔¬∃x(M(x)∧F(x))∀x(¬M(x)∨¬F(x))∀x(M(x)→¬F(x))(量词否定等值式)(???)
后两步结果都是前束范式,说明谓词公式的前束范式不惟一。
(2) ∀ x F ( x ) ∧ ¬ ∃ x G ( x ) \forall x F(x) \land \neg \exist xG(x) ∀xF(x)∧¬∃xG(x)

谓词逻辑中的任一公式都可化为与之等价的前束范式,但其前束范式并不唯一。
求谓词公式的前束范式:
求解过程总结:把各个子式之前的量词换成一个,然后用量词的分配律合起来;
设 G G G 是任一公式,通过下述步骤可将其转化为与之等价的前束范式:
(1) 消去多余的量词;
(2) 约束变元的换名和自由变元的代入;
(3) 消去公式中包含的联结词 → \to →, ⇔ \Leftrightarrow ⇔;
(4) 反复运用德摩根定律,直接将 ¬ \neg ¬ 内移到原子谓词公式的前端;
(5) 使用谓词的等价公式将所有量词提到公式的最前端;
例: 求 ¬ ( ( ∀ x ) ( ∃ y ) P ( a , x , y ) → ( ∃ x ) ( ¬ ( ∀ y ) Q ( y , b ) → R ( x ) ) ) \neg ((\forall x)(\exist y)P(a,x,y) \to (\exist x)(\neg (\forall y)Q(y,b) \to R(x))) ¬((∀x)(∃y)P(a,x,y)→(∃x)(¬(∀y)Q(y,b)→R(x))) 的前束范式。
解:
(1) 消去联结词 → , ⇔ \to,\Leftrightarrow →,⇔,得: ¬ ( ¬ ( ∀ x ) ( ∃ y ) P ( a , x , y ) ∨ ( ∃ x ) ( ¬ ¬ ( ∀ y ) Q ( y , b ) ∨ R ( x ) ) ) \neg (\neg (\forall x) (\exist y) P(a,x,y) \lor (\exist x)(\neg \neg (\forall y) Q(y,b) \lor R(x))) ¬(¬(∀x)(∃y)P(a,x,y)∨(∃x)(¬¬(∀y)Q(y,b)∨R(x)))。
(2) 内移,得: ( ∀ x ) ( ∃ y ) P ( a , x , y ) ∧ ¬ ( ∃ x ) ( ( ∀ y ) Q ( y , b ) ∨ R ( x ) ) ⇔ ( ∀ x ) ( ∃ y ) P ( a , x , y ) ∧ ( ∀ x ) ( ( ∃ y ) ¬ Q ( y , b ) ∧ ¬ R ( x ) ) (\forall x) (\exist y) P(a, x, y) \land \neg (\exist x) ((\forall y) Q(y, b) \lor R(x)) \Leftrightarrow (\forall x) (\exist y) P(a,x,y) \land (\forall x)((\exist y) \neg Q(y,b) \land \neg R(x)) (∀x)(∃y)P(a,x,y)∧¬(∃x)((∀y)Q(y,b)∨R(x))⇔(∀x)(∃y)P(a,x,y)∧(∀x)((∃y)¬Q(y,b)∧¬R(x))
(3) 量词左移,得:
( ∀ x ) ( ( ∃ y ) P ( a , x , y ) ∧ ( ∃ y ) ¬ Q ( y , b ) ∧ ¬ R ( x ) ) ⇔ ( ∀ x ) ( ( ∃ y ) P ( a , x , y ) ∧ ( ∃ z ) ¬ Q ( z , b ) ∧ ¬ R ( x ) ) ⇔ ( ∀ x ) ( ∃ y ) ( ∃ z ) ( P ( a , x , y ) ∧ ¬ Q ( z , b ) ∧ ¬ R ( x ) ) ⇔ ( ∀ x ) ( ∃ y ) ( ∃ z ) S ( a , b , x , y , z ) \begin{align*} &(\forall x)((\exist y) P(a,x,y) \land (\exist y) \neg Q(y, b) \land \neg R(x)) \\ \Leftrightarrow &(\forall x)((\exist y) P(a,x,y) \land (\exist z) \neg Q(z,b) \land \neg R(x)) \\ \Leftrightarrow &(\forall x)(\exist y)(\exist z)(P(a,x,y) \land \neg Q(z,b) \land \neg R(x)) \\ \Leftrightarrow &(\forall x)(\exist y)(\exist z)S(a,b,x,y,z) \end{align*} ⇔⇔⇔(∀x)((∃y)P(a,x,y)∧(∃y)¬Q(y,b)∧¬R(x))(∀x)((∃y)P(a,x,y)∧(∃z)¬Q(z,b)∧¬R(x))(∀x)(∃y)(∃z)(P(a,x,y)∧¬Q(z,b)∧¬R(x))(∀x)(∃y)(∃z)S(a,b,x,y,z)
即: ( ∀ x ) ( ∃ y ) ( ∃ z ) S ( a , b , x , y , z ) (\forall x)(\exist y)(\exist z)S(a,b,x,y,z) (∀x)(∃y)(∃z)S(a,b,x,y,z) 为原式的前束范式,这里 S ( a , b , x , y , z ) S(a,b,x,y,z) S(a,b,x,y,z) 是原公式的母式。
谓词演算的推理理论
设 H 1 , H 2 , ⋯ , H m ( m > 1 ) H_1,H_2,\cdots,H_m(m>1) H1,H2,⋯,Hm(m>1) 和 C C C 都是谓词公式。若 ( H 1 ∧ H 2 ∧ ⋯ H m ) → C (H_1 \land H_2 \land \cdots H_m) \to C (H1∧H2∧⋯Hm)→C 为永真式,即 H 1 ∧ H 2 ∧ ⋯ H m ⇒ C H_1 \land H_2 \land \cdots H_m \Rightarrow C H1∧H2∧⋯Hm⇒C。则称由前提 H 1 , H 2 , ⋯ , H m ( m > 1 ) H_1,H_2,\cdots,H_m(m>1) H1,H2,⋯,Hm(m>1) 推出结论 C C C 的推理正确(有效)。
C C C 称为前提 H 1 , H 2 , ⋯ , H m ( m > 1 ) H_1,H_2,\cdots,H_m(m>1) H1,H2,⋯,Hm(m>1) 的有效结论或逻辑结果。
H 1 , H 2 , ⋯ , H m ( m > 1 ) → C H_1,H_2,\cdots,H_m(m>1) \to C H1,H2,⋯,Hm(m>1)→C 称为由前提 H 1 , H 2 , ⋯ , H m ( m > 1 ) H_1,H_2,\cdots,H_m(m>1) H1,H2,⋯,Hm(m>1) 推出结论 C C C 的推理的形式结构。
谓词逻辑中常用的推理规则其来源可分为两类:
(一) 命题逻辑中的所有推理规则
如规则 P P P, T T T 及 C P CP CP 规则,反证法等亦可在谓词演算的推理中应用,只是应将各规则中的命题公式理解为谓词公式。
谓词演算的推理方法可视为命题演算推理方法的扩张。
(二) 谓词逻辑中特有的推理规则
(1) 谓词演算中与量词有关的基本的永真蕴含式和逻辑等价式;
(2) 量词的消去或添加规则
在谓词演算的推理中,某些前提或结论会受到量词的限制,为了使用命题演算中的等价式和蕴含式,必须有消去或添加量词的规则。
量词的消去或添加规则
全称指定规则( U S US US 规则)
∀ x A ( x ) ⇒ A ( y ) ∀ x A ( x ) ⇒ A ( c ) \begin{gather} \forall x A(x) \Rightarrow A(y) \tag{1}\\ \forall x A(x) \Rightarrow A(c) \tag{2} \end{gather} ∀xA(x)⇒A(y)∀xA(x)⇒A(c)(1)(2)
如果个体域 D D D 中所有的个体都具有性质 A A A,则 D D D 中每一个个体 (个体常元、个体变元) 都具有性质 A A A。
两式成立的条件是:
(1) x x x 是 A ( x ) A(x) A(x) 中自由出现的个体变元。
(2) 在 (1) 式中, y y y 为任意的不在 A ( x ) A(x) A(x) 中约束出现的个体变元,特别地, y y y 可取 x x x。
(3) 在 (2) 式中, c c c 为任意的个体常元。
例: 设个体域 D D D 为实数集,谓词 F ( x , y ) F(x,y) F(x,y): x > y x>y x>y。则 ∀ x ∃ y F ( x , y ) \forall x \exist y F(x,y) ∀x∃yF(x,y): 对任意的实数 x x x,都存在实数 y y y,使 x > y x>y x>y。(真命题)
则下列推理正确的是:()
(1) ∀ x ∃ y F ( x , y ) ⇒ ∃ y F ( c , y ) \forall x \exist yF(x,y) \Rightarrow \exist y F(c,y) ∀x∃yF(x,y)⇒∃yF(c,y)
(2) ∀ x ∃ y F ( x , y ) ⇒ ∃ y F ( x , y ) \forall x \exist yF(x,y) \Rightarrow \exist y F(x,y) ∀x∃yF(x,y)⇒∃yF(x,y)
(3) ∀ x ∃ y F ( x , y ) ⇒ ∃ y F ( y , y ) \forall x \exist yF(x,y) \Rightarrow \exist y F(y,y) ∀x∃yF(x,y)⇒∃yF(y,y)
(4) ∀ x ∃ y F ( x , y ) ⇒ ∃ y F ( z , y ) \forall x \exist yF(x,y) \Rightarrow \exist y F(z,y) ∀x∃yF(x,y)⇒∃yF(z,y)
答案: 1 , 2 , 4 1,2,4 1,2,4正确, 3 3 3 出错的原因是 y y y 已在 ∃ y F ( x , y ) \exist y F(x,y) ∃yF(x,y) 中约束出现。
全称推广规则(UG 规则)
A ( y ) ⇒ ∀ A ( x ) A(y) \Rightarrow \forall A(x) A(y)⇒∀A(x)
如果个体域 D D D 中每一个个体都具有性质 A A A,则 D D D 中所有的个体都具有该性质 A A A 。
该式成立的条件是
(1) y y y 是 A ( y ) A(y) A(y) 中自由个体变元,且 y y y 取个体域 D D D 中的任何值时
A ( y ) A(y) A(y) 均为真。
(2) 取代 y y y 的 x x x 不能是 A ( y ) A(y) A(y) 中的约束变元,否则也会产生错误。
注:使用本规则时,事先必须已经验证了对个体域中的每在个 x x x, A ( x ) A(x) A(x) 都为真。
存在指定规则( E S ES ES 规则)
∃ x A ( x ) ⇒ A ( c ) \exist x A(x) \Rightarrow A(c) ∃xA(x)⇒A(c)
如果个体域 D D D 中存在具有性质 A A A 的个体,则 D D D 中必有某一个个体 c c c (个体常元) 具有该性质 A A A。
该式成立的条件是:
(1) x x x 是 A ( x ) A(x) A(x) 中自由出现的个体变元。
(2) c c c 是使 A ( c ) A(c) A(c) 为真的特定的个体常元,且此 c c c 在该推导前(包括在 A ( x ) A(x) A(x)中) 从未使用过。
(3) 若 A ( x ) A(x) A(x) 中除自由出现的 x x x 以外,还有其他自由个体变元时,不能使用此规则。
例: 设个体域 D D D 为整数集,谓词 F ( x ) : x F(x):x F(x):x 是奇数, G ( x ) : x G(x):x G(x):x 是偶数。
推理过程如下:
(1) ∃ x F ( x ) ⇒ F ( c ) \exist x F(x) \Rightarrow F(c) ∃xF(x)⇒F(c)
(2) ∃ x G ( x ) ⇒ G ( c ) \exist x G(x) \Rightarrow G(c) ∃xG(x)⇒G(c)
则 ∃ x F ( x ) \exist xF(x) ∃xF(x), ∃ x G ( x ) \exist x G(x) ∃xG(x) 都是真命题,但 F ( c ) ∧ G ( c ) F(c) \land G(c) F(c)∧G(c) 假,出错原因: (2) 中的 c c c 已在 (1) 被指定了,已是一个特定的值。(2) 应改为: ∃ x G ( x ) ⇒ G ( d ) \exist x G(x) \Rightarrow G(d) ∃xG(x)⇒G(d), F ( c ) ∧ G ( d ) F(c) \land G(d) F(c)∧G(d) 真。
例: ∃ x F ( x , y ) ⇒ F ( c , y ) \exist x F(x,y) \Rightarrow F(c,y) ∃xF(x,y)⇒F(c,y),出错原因: c c c 的确定还与 y y y 有关。应改为: ∃ x F ( x , y ) ⇒ F ( c y , y ) \exist x F(x,y) \Rightarrow F(c_y, y) ∃xF(x,y)⇒F(cy,y)。
存在推广规则( E G EG EG 规则)
A ( c ) ⇒ ∃ x A ( x ) A(c) \Rightarrow \exist x A(x) A(c)⇒∃xA(x)
A ( y ) ⇒ ∃ x A ( x ) A(y) \Rightarrow \exist x A(x) A(y)⇒∃xA(x)
如果个体域 D D D 中某个个体 (个体常元、个体变元)具有性质 A A A,则 D D D 中存在着具有该性质 A A A 的个体。
两式成立的条件是
(1) c c c 是使 A ( c ) A(c) A(c) 为真的特定的个体常元。
(2) y y y 是使 A ( y ) A(y) A(y) 为真的自由个体变元。
(3) 取代 c c c 或 y y y 的 x x x 不能在 A ( c ) A(c) A(c) 或 A ( y ) A(y) A(y) 中出现过。
例: 设个体域 D D D 为实数集
(a) 谓词 F ( x , y ) F(x,y) F(x,y): x > y x>y x>y
则下列推理正确的是:
(1) ∃ x F ( x , y ) ⇒ ∀ z ∃ x F ( x , z ) \exist x F(x,y) \Rightarrow \forall z \exist x F(x,z) ∃xF(x,y)⇒∀z∃xF(x,z)
(2) ∃ x F ( x , y ) ⇒ ∀ x ∃ x F ( x , x ) \exist x F(x,y) \Rightarrow \forall x \exist x F(x,x) ∃xF(x,y)⇒∀x∃xF(x,x)
1对2错
(b) 谓词 F ( x , y ) F(x,y) F(x,y): x ∗ y = 0 x*y=0 x∗y=0
则下列推理正确的是:
(1) ∀ x F ( x , 0 ) ⇒ ∃ x ∀ x F ( x , x ) \forall x F(x,0) \Rightarrow \exist x \forall x F(x,x) ∀xF(x,0)⇒∃x∀xF(x,x)
(2) ∀ x F ( x , 0 ) ⇒ ∃ z ∀ x F ( x , z ) \forall x F(x,0) \Rightarrow \exist z \forall x F(x,z) ∀xF(x,0)⇒∃z∀xF(x,z)
1错2对
使用时的注意事项:
(1) 量词的消去或添加规则只对前束范式(即辖域为整个公式)的量词成立,不能对出现在公式中间的量词使用它们。
(2) 使用时,要严格按照限制条件去使用,并从整体上考虑个体常元和个体变元符号的选择。
(3) 用 y y y 或 c c c 取代 A ( x ) A(x) A(x) 中自由出现的 x x x 时,一定要在 x x x 自由出现的每一处都取代。
数理逻辑总结
命题公式中的命题变元的最小粒度是命题。命题公式中的命题变元之间,可以通过下面的联结词来联结。
否定联结词: ¬ \neg ¬,非
合取联结词: ∧ \land ∧ 与、且
析取联结词: ∨ \lor ∨,或
条件联结词: → \to →,“若…则…”“如果…就."“只有…才…”
等价联结词(双条件联结词): ↔ \leftrightarrow ↔,当且仅当
并析交合。
命题公式的等价: ⇔ \Leftrightarrow ⇔
命题公式的蕴含: ⇒ \Rightarrow ⇒
谓词公式的等价: ⇔ \Leftrightarrow ⇔
谓词公式的蕴含: ⇒ \Rightarrow ⇒
分析一个命题中的谓词可以构成一个命题函数,函数的参数是客体。
命题公式没有真值但是有真值表。
- 什么时候翻译成命题公式?
- 什么时候翻译成命题函数?
- 谓词逻辑翻译技巧:主系表中的系表是谓词,表性质;主谓宾中的谓语是谓词,表主和宾的关系。