上图代码是出自雷神之锤3计算一个正实数的算术平方根的倒数的算法，一般我们去计算一个数的平方根采用最好的方法是牛顿迭代法

不会牛顿迭代法，可以去看下这位大哥的帖子

www.cnblogs.com/houkai/p/3332520.html

比如我们要求 x 的平方根倒数，就可以构造一个关于y的函数      

把这个函数代入牛顿迭代公式里面就可以求出迭代形式

                                

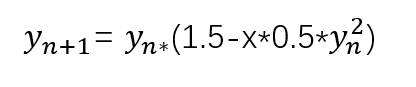
这就是第 5、6、11 行代码的由来，我们知道通过上图公式一直迭代计算下去，这个函数在处有收敛，此时 y  的值即为所求

 牛顿迭代法计算平方根的倒数，如果迭代次数过多，会影响计算机性能，那么能不能在这个收敛值的附近先找出一个预解值出来，从而快速计算到收敛值，减少迭代次数减少计算量？这个思想从而就引出了这个神迹代码，也就是整个代码的核心思想，这个预解值就是用第8、9、10这三行代码计算出来

 第8行代码：先将要求的浮点数转换成浮点数二进制表示法下的整数，不会浮点数二进制表示法可以去看看这位大哥的帖子 

blog.csdn.net/wangshuaiwsws95/article/details/105874684

第9行代码：将转换成整数的值除以2，也就是 i>>1 往右移动一位，再用0x5f3759df这个常数去减它

第10行代码：将第9行代码求出来的整数值强制转换成浮点数，这样就得到了一个预解值，牛顿迭代一次精度可到小数点后三位。

非常神奇！

大家对这个代码的理解基本上来自维基百科上的解释！可以去看这位大哥的帖子

blog.csdn.net/weixin_43899202/article/details/120540104

本人从另外一个角度来考虑了这个问题：

按照浮点数二进制表示法，一个任意大于0（小于等于0在计算机中不能开根号）能存储在32位的浮点数转换成二进制整数时，至少是   这个数，第9行代码明显是一个一次函数，浮点数曲线函数转换成二进制整数时，把这条曲线放大了很多倍，当成一条直线去计算，当然这种放大并不是线性的放大。

一条曲线无限放大就是一条模糊直线，可以通过最小二乘法去计算这条模糊直线的解析式，早就有的数学模型，也就是古人说的天圆地方，地球是平的

 这个幂函数在浮点数二进制表示成整数后，把这个曲线函数放大后转换成了一次函数y=-0.5x+0x5f3759df，计算完成再缩回去，把32位二进制整数再变回浮点数。

浮点数转二进制整数、二进制整数转浮点数  ：这种转换关系应该就是函数与反函数的转换关系。

                                                             最小二乘法公式：

                                                      

 

                                       有了上面这个思路 于是我在找了一串数

总共45组浮点数转换成二进制整数表示，再代入最小二乘法公式中求得直线方程为

不可能再将整数转成浮点数再去计算，所以舍去一些精度，斜率值定在0.5，常数值1597492524比0X5f3759df精度要差一些

其实没有绝对精度的常数值，斜率不变，只动常数值，直线会左移或者右移，只要不太偏离这条模糊直线，在某些数值区域总有精度你比我高，或者我比你高，看谁高的区域多些，就认为哪个常数值比较好！

当我去掉   这组数时，斜率值是-0.500001819，此时常数值是1597292554.53

当我再去掉  这组数时，斜率值是-0.49999941，此时常数值是1597289491.83

因此我认为最佳值应该在 1597289491.83-1597292554.53之间，

依据斜率值与常数值的线性关系计算，最佳常数值应该是1597289588转换成16进制0x5F34B474

穷举了下0x5f3759df和0x5f34b474 在1-1000000之间，看谁的精度次数高，代码如下

 明显0x5f34b474精度要高出一倍多

至于0x5f3759df 这个神秘常数的由来，我也搞不清楚！

大家可以依据此方法去计算64位浮点下计算平方根倒数的常数或者开平方根、立方根等一些曲线函数的计算常数！

计算要用EXCEL去算，计算数值太大，C语言64位整数装不下！

由于芯片技术的发展，SIMD等矢量指令集的出现，此计算方法已成为时代的产物，但是前辈大佬的脑洞大开，为我们展示了数学之美！！！！！！！,向发明此算法的大佬致敬！！！！！！！！