信号处理中简单实用的方法—

数字滤波器的输出有瞬态效应，即当取有限长的信号时对信号的截断，会使输出信号的前端产生失真；当通过零相位滤波器时，由于信号通过滤波器二次，会使输出信号的两端都产生失真。有些文献报道为改善滤波器输出的失真，则在原始信号滤波前进行延拓。在希尔伯特变换和EMD变换中也有端点效应，也有文献提出先进行延拓后再作变换。下面将介绍如何用自回归模型的方法进行数据延拓。

1.求自回归系数1
名称：lpc
功能：求一数据序列的自回归系数
调用格式：
ar=lpc(x,p)

说明：x是数据序列；p是计算自回归的阶数；ar是自回归系数，或称为预测系数。函数
1pc是MATLAB自带的。本函数是按上述的莱文逊-杜宾算法计算出自回归系数。

2.求自回归系数2
名称：arburg
功能：求一数据序列的自回归系数
调用格式：
ar =arburg(x,p)

说明：x是数据序列；p是计算自回归的阶数；ar是自回归系数。函数arburg也是MATLAB自带的。本函数是按burg算法计算出自回归系数[5]，由于在burg算法中计算前向和后向误差，所以比莱文逊一杜宾算法有更高的精度。

3.前向预测
名称：for_predict
功能：求一数据序列的前向预测数据
调用格式：
y=for_predictm(x,N,p)

说明：x是数据序列；N是往前预测的样点数；P是计算自回归的阶数；y是预测出N个样点值。前向预测函数、后向预测函数以及前向-后向预测函数都是宋知用老师自编的。程序如下：

function y=for_predictm(x,N,p)
x=x(:);                 % 把x转为列序列
M=length(x);            % x长度
L=M-p;                  % 设置前向预测位置
ar=arburg(x,p);         % 计算自回归求得ar
xx=x(L+1:L+p);          % 准备前向预测的序列
for i=1:N               % 朝前预测得N个数xx(p+i)=0;          % 初始化for k=1:p           % 按式(4-6-3)累加xx(p+i)=xx(p+i)-xx(p+i-k)*ar(k+1);end
end
y=xx(p+1:p+N);          % 得前向预测的序列

4.后向预测
名称：back_predict
功能：求一数据序列的后向预测数据
调用格式：
y=back_predictm(x,M,p)

说明：x是数据序列；M是往后预测的样点数；P是计算自回归的阶数；y是预测出M个样点值。程序如下：

function y=back_predictm(x,M,p)
x=x(:);                 % 把x转为列序列
ar1=arburg(x,p);        % 计算自回归求得ar
yy=zeros(M,1);          % 初始化
yy=[yy; x(1:p)];        % 准备后向预测的序列
for l=1 : M             % 朝后预测得M个数for k=1 : p         % 按式(4-6-27)累加yy(M+1-l)=yy(M+1-l)-yy(M+1-l+k)*ar1(k+1);endyy(M+1-l)=real(yy(M+1-l));
end
y=yy(1:M);              % 得后向预测的序列

5.前向-后向预测
名称：forback_predict
功能：求一数据序列的前向和后向的预测数据序列
调用格式：
x=forback_predictm(y,L,p)

说明：y是数据序列；L是往前预测及往后预测的样点数；p是计算自回归的阶数；x是前向预测出L个样点值、后向预测出L个样点值与数据y一起合并成的列向数据序列。程序如下：

function x=forback_predictm(y,L,p)
y=y(:);                      % 把y转为列序列
u1=back_predictm(y,L,p);     % 计算后向延拓序列
u2=for_predictm(y,L,p);      % 计算前向延拓序列
x=[u1; y; u2];               % 把前后向预测与y合并成新序列

一、消除信号经零相位滤波后两端的瞬态效应

前面已经说明了滤波后的数据一般都会在输出信号的初始端有瞬态效应，而零相位滤波是正向和反向两次通过滤波器，所以在输出信号的两端都会有瞬态效应。下面利用对信号两端延拓，消除这瞬态效应的影响。

案例1、有一个信号由直流分量与3个交流分量组成：x(n)=100+10sin（2πf1t)+10sin(2πf2t)+10sin（2πf3t),f1=0.001Hz为低频信号，f2=5Hz和f3=50Hz为工频信号，采样频率fs=1000Hz，样点数为1000。设计一个巴特沃斯带通滤波器，通过零相位滤波得到5Hz的信号分量，并将不用延拓和用延拓两种方法的滤波器输出与原信号进行对比。程序如下：

clear all; clc; close allN = 1000;                    % 数据长度
Fs = 1000;                   % 采样频率
t = (0:N-1)/Fs;              % 时间刻度
% 滤波器设计
fp=[3 15];                   % 滤波器通带阻带参数设定
fs = [0.5 30];
rp = 1.5;                    % 通带波纹
rs = 20;                     % 阻带衰减
wp = fp*2/Fs;                % 归一化频率
ws = fs*2/Fs;
[n,wn]=buttord(wp,ws,rp,rs); % 计算滤波器阶数
[b,a] = butter(n,wn);        % 计算滤波器系数
[h,w] = freqz(b,a,1000,Fs);  % 求滤波器响应
h = 20*log10(abs(h));        % 计算滤波器幅值响应 %信号的产生
f1 = 0.001;                  % 分量1,准直流
f2 = 5;                      % 分量2,有用信号
f3 = 50;                     % 分量3,工频干扰
x1 = 100+10*sin(2*pi*f1*t);  % 产生3个分量的信号
x2 = 10*sin(2*pi*f2*t);
x3 = 10*sin(2*pi*f3*t);
xn = x1+x2+x3;               % 合并为信号xn
y1=filtfilt(b,a,xn);         % 做零相位带通滤波
Segma1=var(y1-x2);           % 计算方差
L=400;                       % 设置延拓长度
yn=forback_predictm(xn,L,10);% 前后向延拓
ynt = filtfilt(b,a,yn);      % 做零相位带通滤波
y2 = ynt((L+1):(L+N));       % 消去延拓部分
Segma2=var(y2'-x2);          % 计算方差
fprintf('Segma1=%5.4f   Segma2=%5.4f\n',Segma1,Segma2);
% 作图
figure(1)
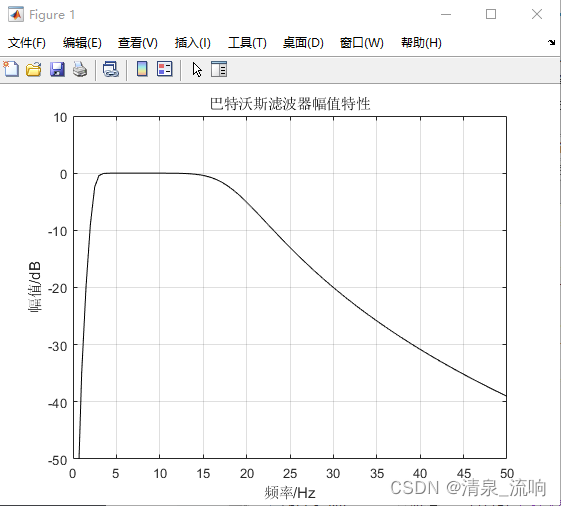
plot(w,h,'k');
grid; axis([0 50 -50 10]);
title('巴特沃斯滤波器幅值特性')
ylabel('幅值/dB');xlabel('频率/Hz');
set(gcf,'color','w');
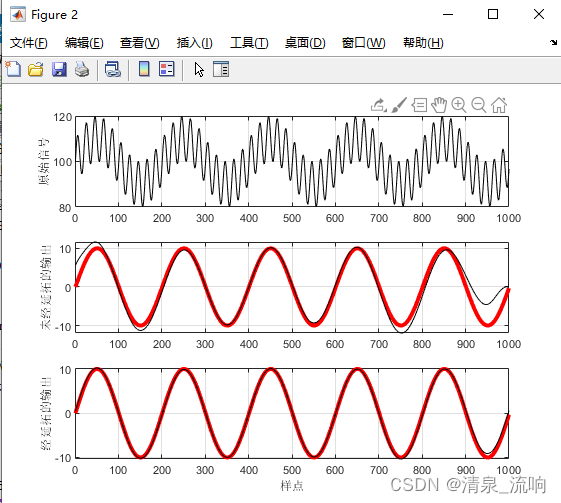
figure(2)
n=1:N;
subplot 311; plot(n,xn,'k'); 
grid; ylabel('原始信号')
subplot 312; plot(n,x2,'r','linewidth',3); hold on;
plot(n,y1,'k'); grid;
ylabel('未经延拓的输出')
subplot 313; plot(n,x2,'r','linewidth',3); hold on;
plot(n,y2,'k'); grid;   xlabel('样点')
ylabel('经延拓的输出')
set(gcf,'color','w');

运行结果如下：

①在本程序中，延拓长度取为L=400样点。延拓长度主要是和提取的频率有关，对延拓长度L和阶数p值都要取适当的值。
②为了比较没经过延拓及经过延拓在零相位滤波后有什么差别，在这两种情形中的滤波输出都计算了与原始数据差值的方差值。
③在延拓时把数据变长了，在滤波器输出中要把延拓部分消除，恢复数据原始的长度。

从图中可看出，数据未经延拓通过零相位滤波器输出的波形两端与原始数据波形有明显偏差，而数据经延拓后通过零相位滤波器输出的波形与原始数据波形基本重合在一起。计算出的方差值如下：数据未经延拓的输出方差Segmal=3.4332，数据经延拓的输出方差Segma2=0.0927。由此可知，经延拓后滤波使误差要小许多。

二、消除希尔伯特变换的端点效应

在希尔伯特变换后，波形两端也经常会发生失真现象，通过端点延拓可以解决这一问题，下面将介绍端点延拓在希尔伯特变换中的应用。

案例2、信号x由两个频率的正弦组成，求x的希尔伯特变换，比较没有延拓和有延拓的结果。采样频率为1000Hz，数据长1000，信号的两个频率为f1=5Hz和f2=50 Hz。程序如下：

clear all; clc; close all;Fs=1000;                     % 采样频率
N=251;                       % 样点数
t=(0:N-1)/Fs;                % 时间刻度f1=10; f2=21;                % 信号频率f1和f2
L=20;                        % 延拓长度
ys=sin(2*pi*f1*t)+sin(2*pi*f2*t);  % 正弦信号
yc=cos(2*pi*f1*t)+cos(2*pi*f2*t);  % 余弦信号
x1=forback_predictm(ys,L,4);        % 延拓
hys=hilbert(ys);             % 求没有延拓时的希尔伯特变换
hx1=hilbert(x1);             % 求延拓后序列的希尔伯特变换
hys1=hx1(L+1:L+N);           % 消去延拓的增长
% 作图
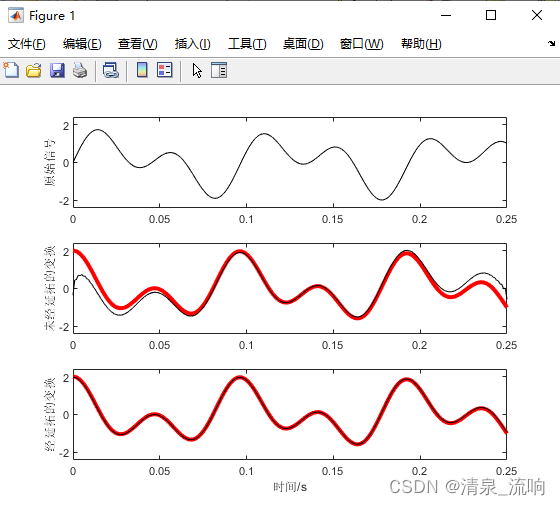
subplot 311; plot(t,ys,'k'); 
axis([0 max(t) -2.4 2.4]); ylabel('原始信号')
subplot 312; plot(t,yc,'r','linewidth',3); hold on
plot(t,-imag(hys),'k'); axis([0 max(t) -2.4 2.4]);
ylabel('未经延拓的变换')
subplot 313; plot(t,yc,'r','linewidth',3); hold on
plot(t,-imag(hys1),'k'); axis([0 max(t) -2.4 2.4]);
ylabel('经延拓的变换'); xlabel('时间/s')
set(gcf,'color','w');

运行结果如下：