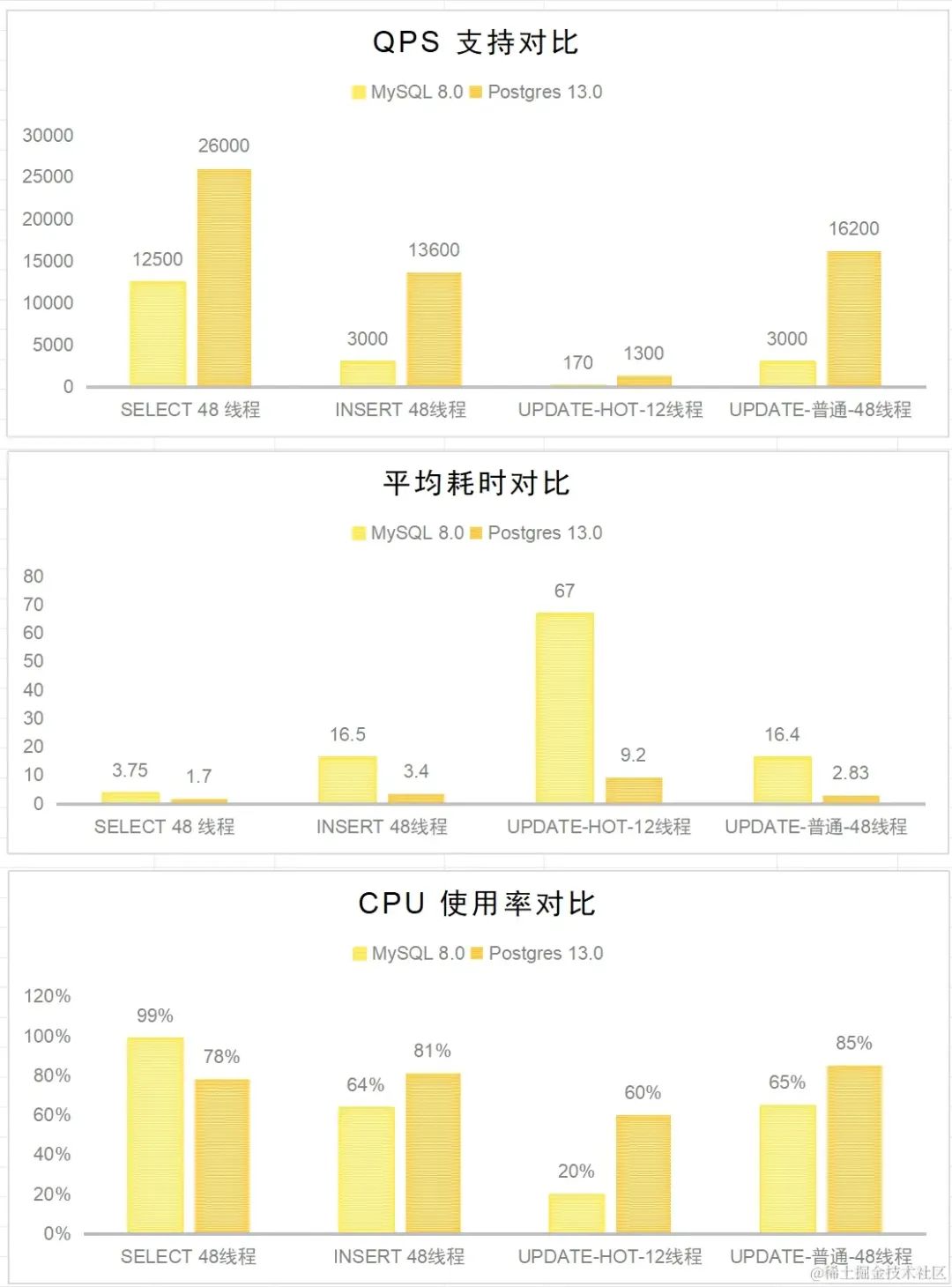
题目描述

编程计算由"1"围成的下列图形的面积。面积计算方法是统计"1"所围成的闭合曲线中"0"点的数目。如图所示，在10*10的二维数组中，"1"围住了15个点，因此面积为15。

提示：queue

输入

测试次数t

每组测试数据格式为：

数组大小m,n

一个由0和1组成的m*n的二维数组

输入样例：

2
10 10
0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 1 0 0 0
0 0 0 0 1 0 0 1 0 0
0 0 0 0 0 1 0 0 1 0
0 0 1 0 0 0 1 0 1 0
0 1 0 1 0 1 0 0 1 0
0 1 0 0 1 1 0 1 1 0
0 0 1 0 0 0 0 1 0 0
0 0 0 1 1 1 1 1 0 0
0 0 0 0 0 0 0 0 0 0
5 8
0 1 1 0 0 1 1 0
1 0 1 0 1 0 0 1
0 1 0 1 0 0 1 0
0 1 0 0 1 1 1 0
0 0 0 0 0 0 0 0

输出

对每个二维数组，输出符号"1"围住的"0"的个数，即围成的面积。假设一定有1组成的闭合曲线，但不唯一。

输出样例：

15
5

代码

#include <iostream>
#include <queue>
using namespace std;class List{
public:int m,n;int **matrix,**flag;  //matrix矩阵， flag标志是否入过队List(){cin >> m >> n;matrix = new int*[m+2];  //将原本的矩阵周围新增一圈行列，防止路径被边缘的1堵死flag = new int*[m+2];for(int i = 0; i < m+2; i++){matrix[i] = new int[n+2];flag[i] = new int[n+2];for(int j = 0; j < n+2; j++){if(i == 0 || i == m+1 || j == 0 || j == n+1){matrix[i][j] = 0;  //边缘一圈的赋值0}else{cin >> matrix[i][j];}flag[i][j] = 0;  //初始化}}}void BFS(){  //用广度优先搜索遍历矩阵中不被包围的0，将其改为1，即将矩阵中所有不被1包围的0改成1queue<int> queX,queY;  //queX存储横坐标，queY存储纵坐标int x,y;queX.push(0);queY.push(0);flag[0][0] = 1;while(!queX.empty()){  //即队列非空时x = queX.front();y = queY.front();matrix[x][y] = 1;queX.pop();queY.pop();if(x+1 < m+2){  //对当前队首元素构成的坐标按照上下左右的顺序广度搜索if(matrix[x+1][y] == 0 && flag[x+1][y] == 0){  //此句一定要和上面的if分开queX.push(x+1);queY.push(y);flag[x+1][y] = 1;}}if(x-1 >= 0){if(matrix[x-1][y] == 0 && flag[x-1][y] == 0){queX.push(x-1);queY.push(y);flag[x-1][y] = 1;}}if(y+1 < n+2){if(matrix[x][y+1] == 0 && flag[x][y+1] == 0){queX.push(x);queY.push(y+1);flag[x][y+1] = 1;}}if(y-1 >= 0){if(matrix[x][y-1] == 0 && flag[x][y-1] == 0){queX.push(x);queY.push(y-1);flag[x][y-1] = 1;}}}}int getRes(){  //遍历矩阵，累加为0的元素个数int sum=0;for(int i = 1; i < m+1; i++){for(int j = 1; j < n+1; j++){if(matrix[i][j] == 0){sum++;}}}return sum;}
};int main()
{int t,res;cin >> t;while(t--){List list;list.BFS();res = list.getRes();cout << res << endl;}return 0;
}