
- 博主简介:努力学习的22级计算机科学与技术本科生一枚🌸
- 博主主页: @Yaoyao2024
- 每日一言🌼: 勇敢的人,不是不落泪的人,而是愿意含着泪继续奔跑的人。
——《朗读者》

0、声明
本系列博客文章是博主本人根据吴恩达老师2022年的机器学习课程所学而写,主要包括老师的核心讲义和自己的理解。在上完课后对课程内容进行回顾和整合,从而加深自己对知识的理解,也方便自己以及后续的同学们复习和回顾。
- 课程地址👉🏻2022吴恩达机器学习Deeplearning.ai课程
- 课程资料和代码(jupyter notebook)👉🏻2022-Machine-Learning-Specialization
由于课程使用英文授课,所以博客中的表达也会用到英文,会用到中文辅助理解。
🌸Machine learning specialization课程共分为三部分
- 第一部分:Supervised Machine Learning: Regression and Classification
- 第二部分:Advanced Learning Algorithms(Neural networks、Decision Trees)
- 第三部分:Unsupervised Learning: Recommenders, Reinforcement Learning
💐最后,感谢吴恩达老师Andrew Ng的无私奉献,和视频搬运同学以及课程资料整合同学的无私付出。Cheers!🍻
前言
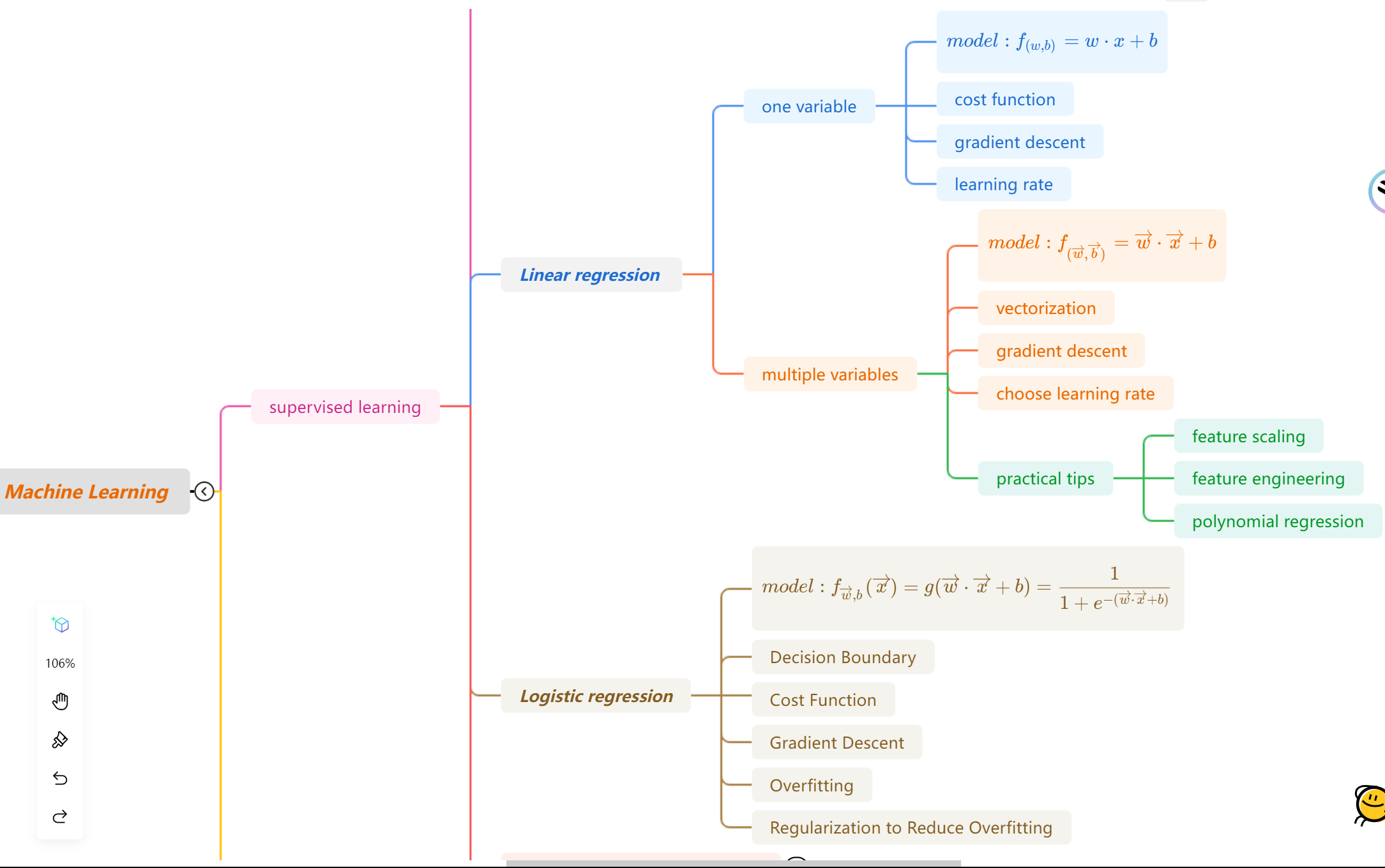
🪧在前两章中,我们学习了线性回归模型(单变量、多变量)。线性回归模型主要是解决回归任务。我们知道,监督学习(Supervised Learning)中,还有一个重要的任务:分类(classification) 。分类问题的主要思路和模型训练过程和回归任务类似。但是在模型的选择和算法思想上还是有一些不同的。我们下面会从线性回归模型引入,介绍适用于分类任务的模型:逻辑回归模型(logistic regression model).并介绍基于它的代价函数、梯度下降。此外还会引入及存在于回归任务又存在于分类任务中的两个概念:过拟合(Overfitting)、正则化(Regularization)。
💁🏻♀️接下来让我们开始吧!💐🚂🚂🚂
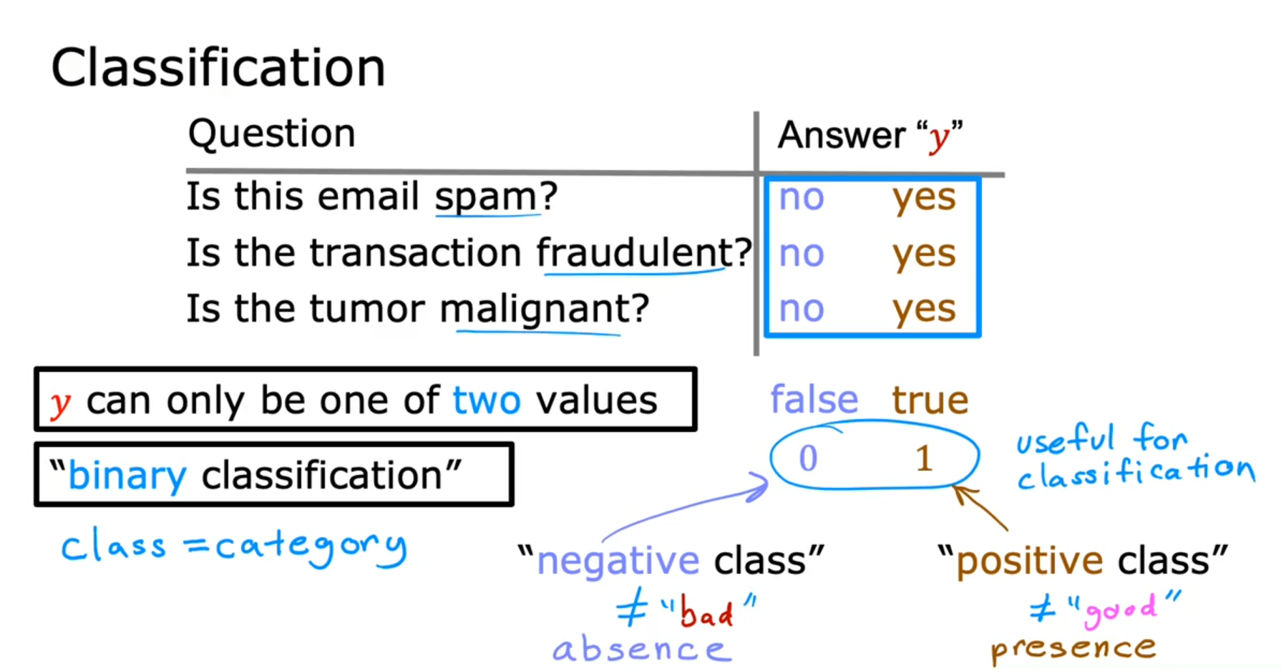
一、分类问题引入
下面图中展示的是二分类问题。可以看到,数据的形式和线性回归模型很类似。不同点就在于目标值y是离散的两个值,而非连续。
如果借用回归模型的思想,我们其实也可以拟合一个线性函数:
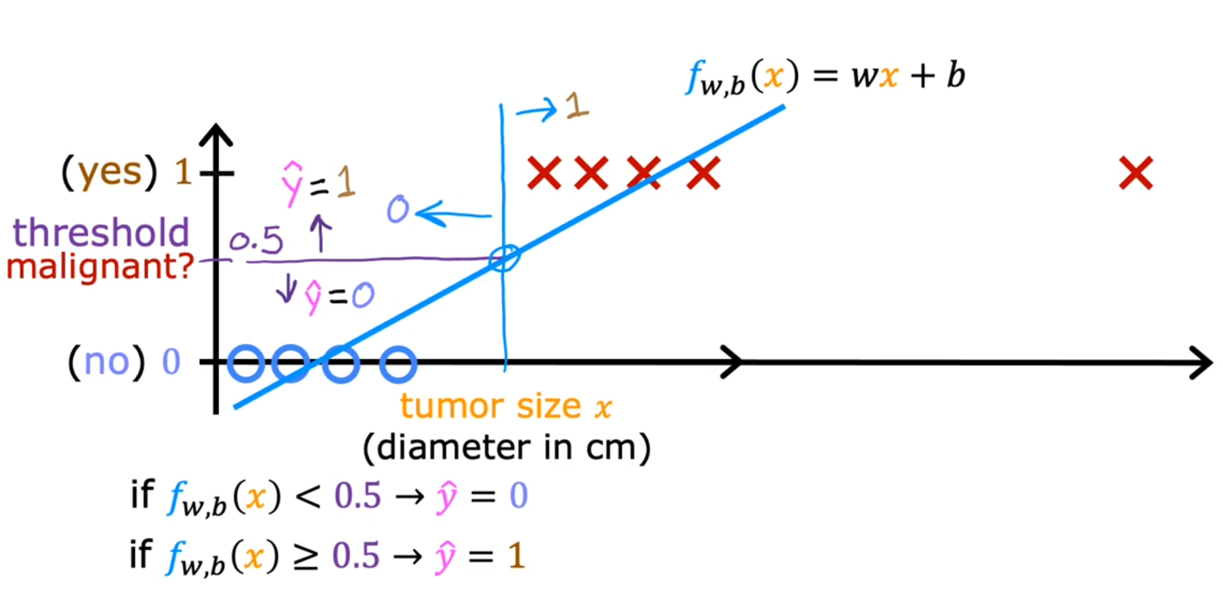
上图可以看出:线性回归模型+阈值,似乎就能解决分类问题。但真的如此吗?
下图可以看到,当增加数据时,模型按照线性回归模型的训练方法,会有所改变。但是改变之后模型更加糟糕。
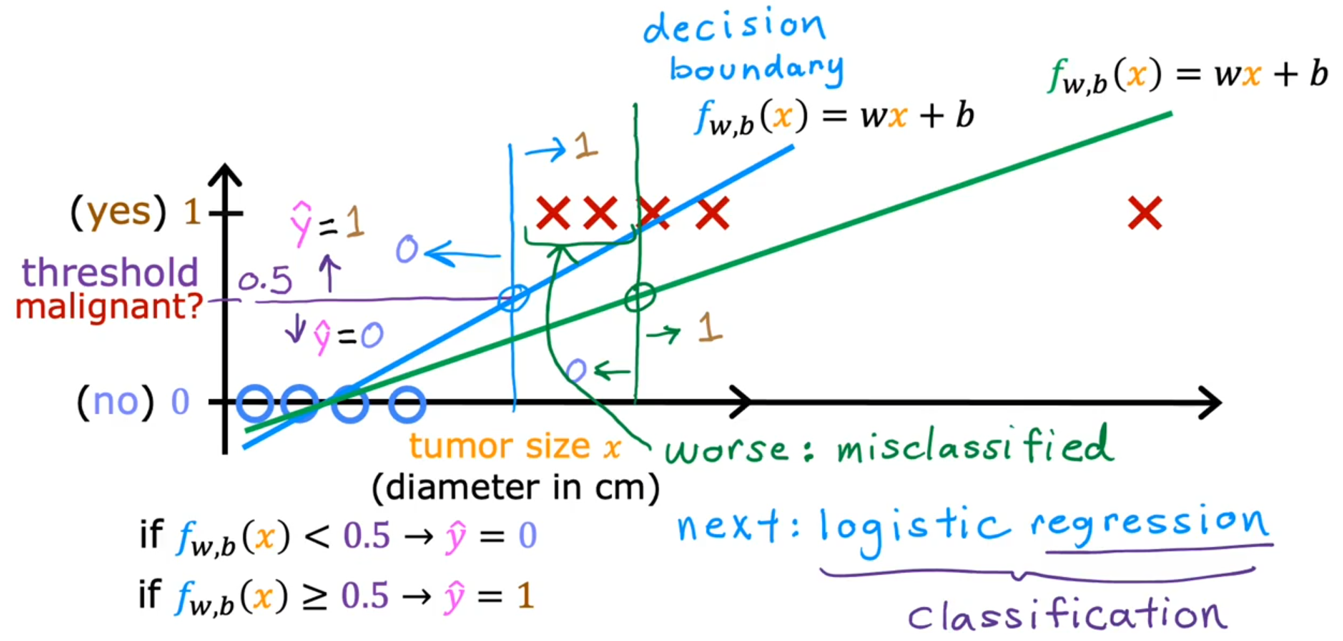
💁🏻♀️总结:分类问题肯定不是简单的线性回归+阈值分割。
二、逻辑回归模型
于是,提出了逻辑回归模型。核心思想还是:回归+阈值分割。
在这个模型中的一个关键是: 逻辑函数(logistic function):Sigmoid 函数
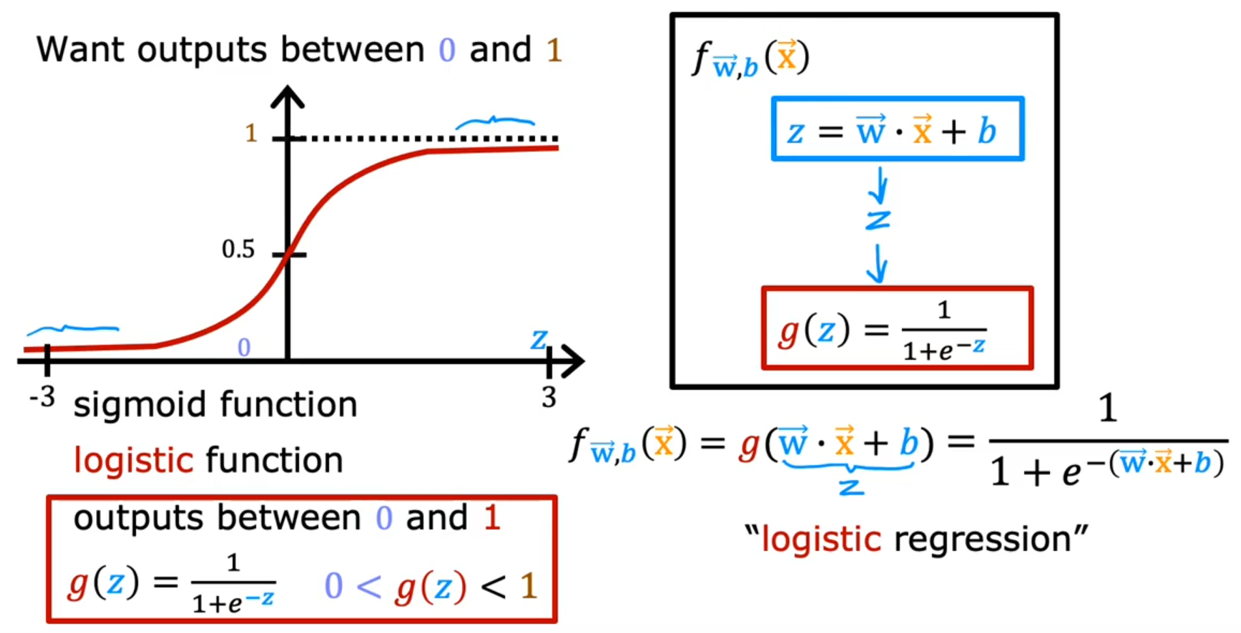
上图可以看到,对比线性回归模型,Sigmod函数套在线性回归函数的外面,作用像是把线性函数掰弯然后再捋平后。将取值范围从(-∞ ~ +∞)映射到(0~1)。更好的表示了分类问题中,对分类类别的可能性预测——概率。
下图展示了对逻辑回归模型中输出变量的解释。可以看到,输出值就是类别为1时,在给定输入变量和参数的情况下的概率。

2.1:决策边界(Decision Boundary)
下图是是逻辑回归模型的具体步骤,可以看到。首先是预测回归模型的值(类别为1的概率),再进行阈值分割(阈值为0.5)。也印证了前面说的,分类问题的本质还是回归+阈值分割。
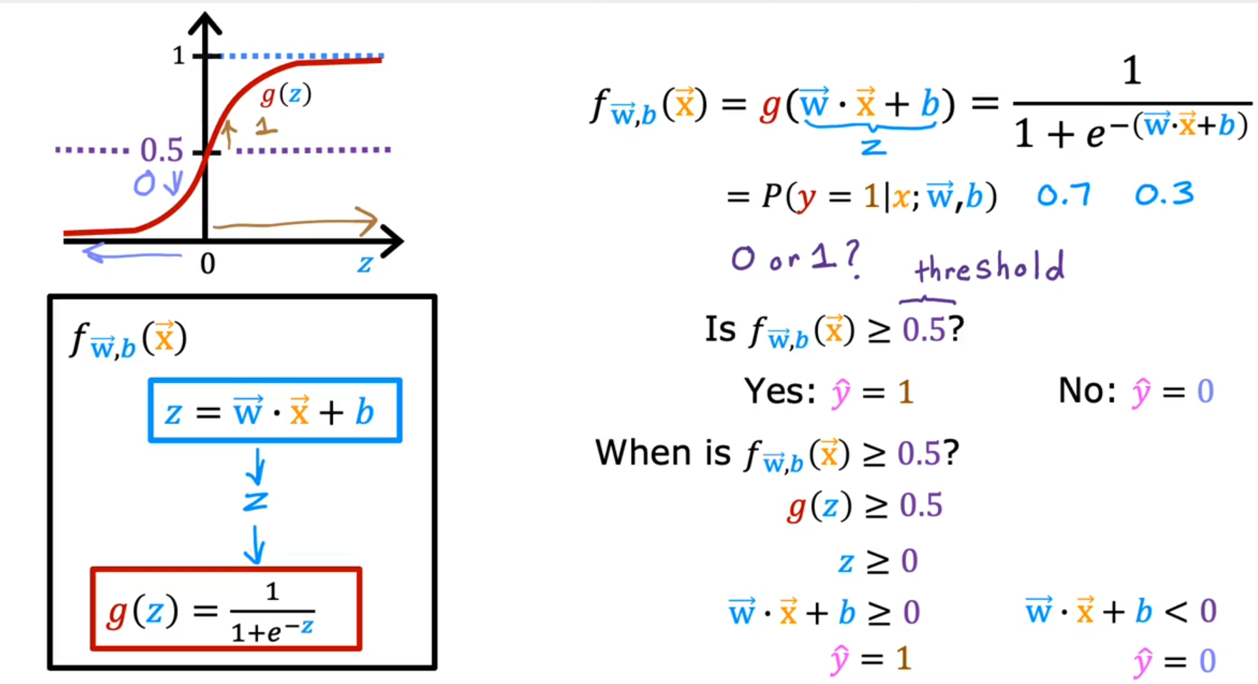
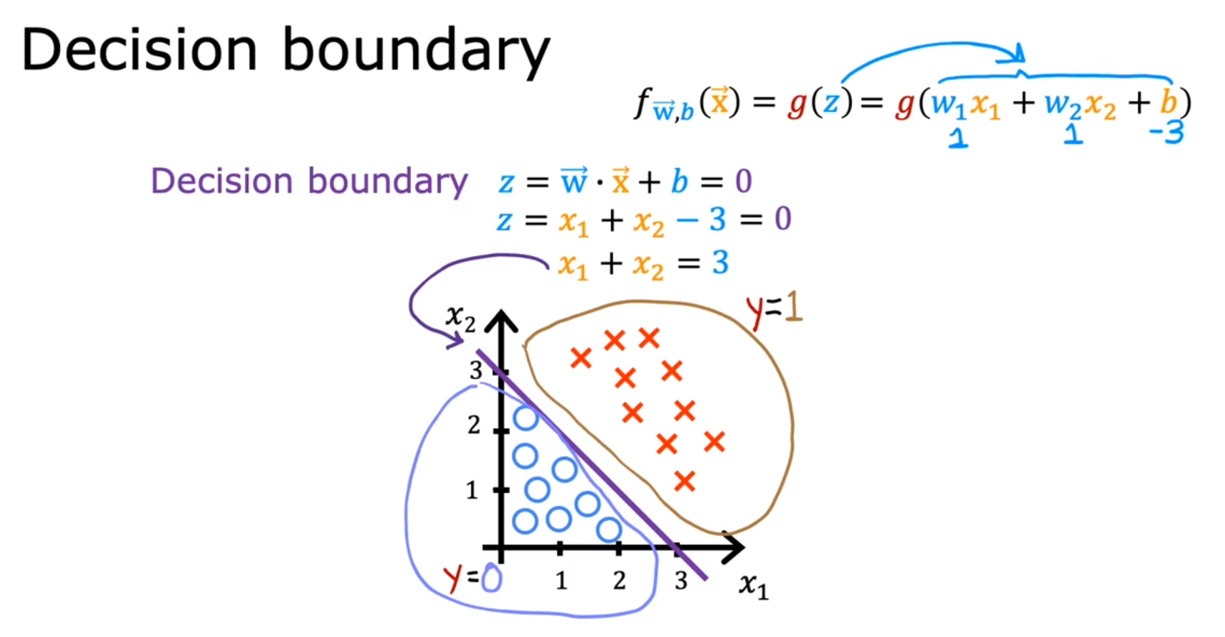
由上图也可知,在逻辑回归模型中,阈值0.5的取得是当z=0时。当回归函数z=0时,映射到嵌套的回归函数中,对应的就是:决策边界(Decision Boundary).
就像下面这样:当回归函数z >= 0,也就是在决策边界“之上”时,代表类别为1.
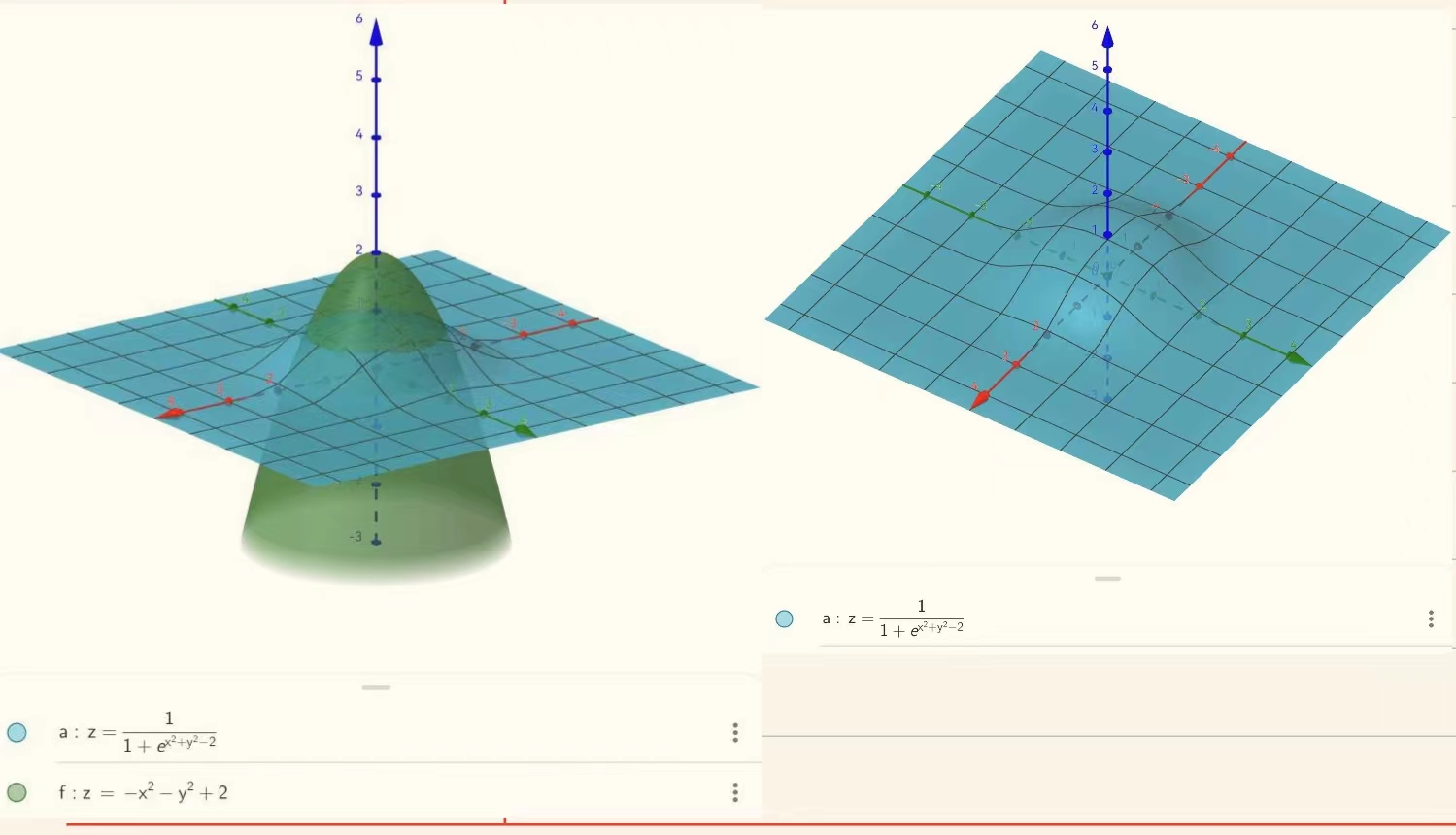
下面是非线性的回归函数z展示。绿色的部分就是回归边界,绿色部分>=0时表示类别为1
2.2:损失函数(loss) & 代价函数(cost)
在前一章中训练线性回归模型时我们学过均方误差代价函数,它是衡量训练集中样本数据的真实目标值和对应的预测值之间的拟合程度的。
线性回归模型中运用的代价函数是 基于距离度量的。即把目标数据和预测数据映射到距离度量的特征空间中(如欧氏空间,汉明空间等),将映射后的样本数据看作是空间中的点,再运用损失函数(loss function)来度量两点之间的距离。这个举例也代表这两个点的拟合程度。 将目标值和预测值映射,放到特征空间的两点中,运用损失函数度量样本真实目标值和模型预测值之间的距离。特征空间中两个点度量的距离越小,模型预测性能越好。
上面提到的损失函数(loss function),函数形式和代价函数形式一致。损失函数的定义就是针对单个样本来说的,求单个样本的目标值和预测值之间的距离。而代价函数(成本函数)是针对整个样本集来说的,可以理解为整个样本集的损失函数的累加和再平均。
💁🏻♀️ 选择损失函数的两个关键点:
- 整体的代价函数是凸的(保证能够正确的进行梯度下降,得到理想参数值)
- 满足损失函数的定义:
- 预测值接近真实值,loss➡∞
- 预测值远离真实值,loss➡0
基于距离的均方误差损失函数并不适用于分类问题的逻辑回归模型。如下图,因为用它求出来的代价函数不满足整个代价函数是凸的:

在分类任务中逻辑回归模型是运用 基于概率分布度量的损失函数: 交叉熵损失函数
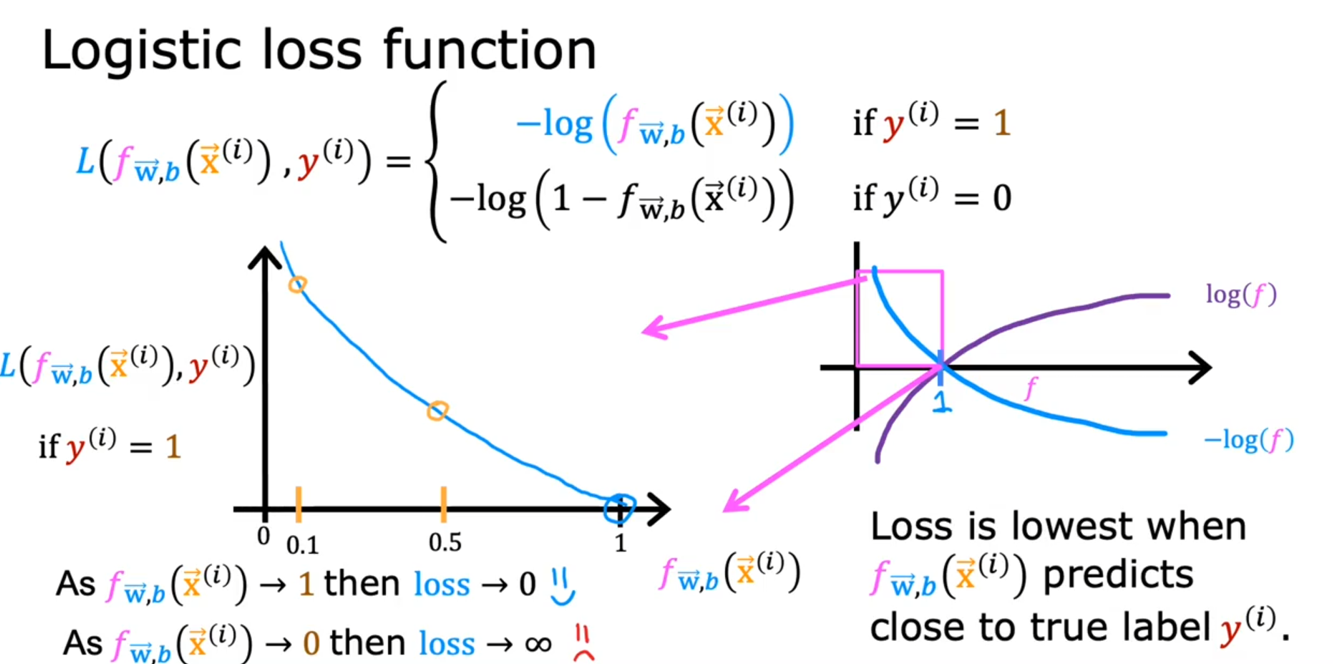
ps:背后是使用概率论中的最大似然估计求得的,这里可以不用管这个背后的原理。
也可以像下面这样直接写成一个式子:
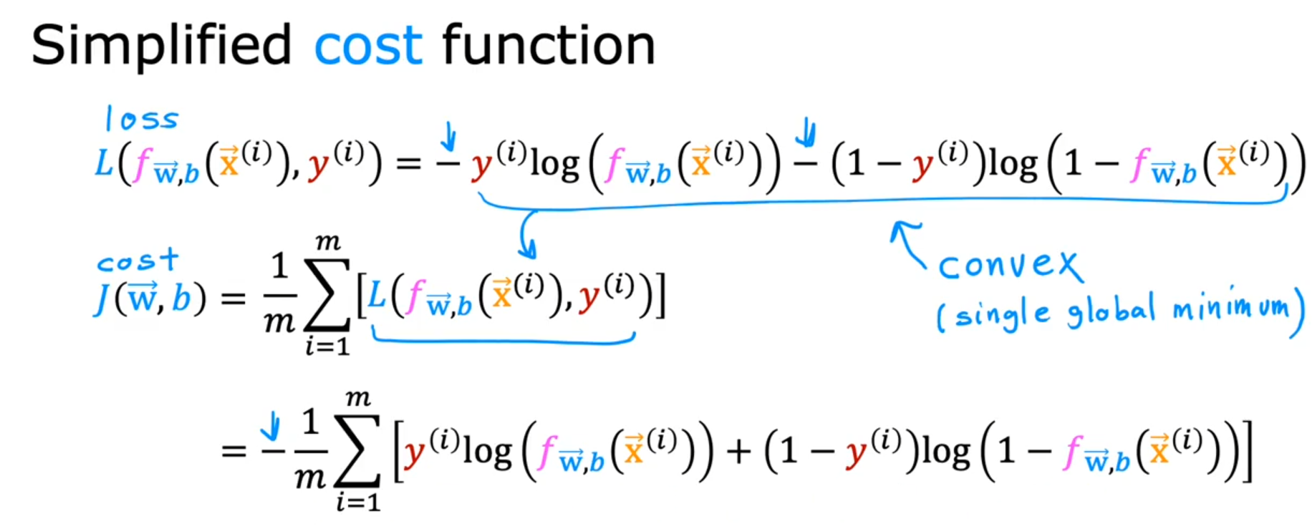
2.3:梯度下降
梯度下降和一些在多变量回归模型那章提出的一些concepts的主要思想,在逻辑回归中仍然适用:


三、正则化(Regularization)
3.1:引入:过拟合问题(Overfitting)
下图可以看到,当模型参数过多时,会出现过拟合问题。
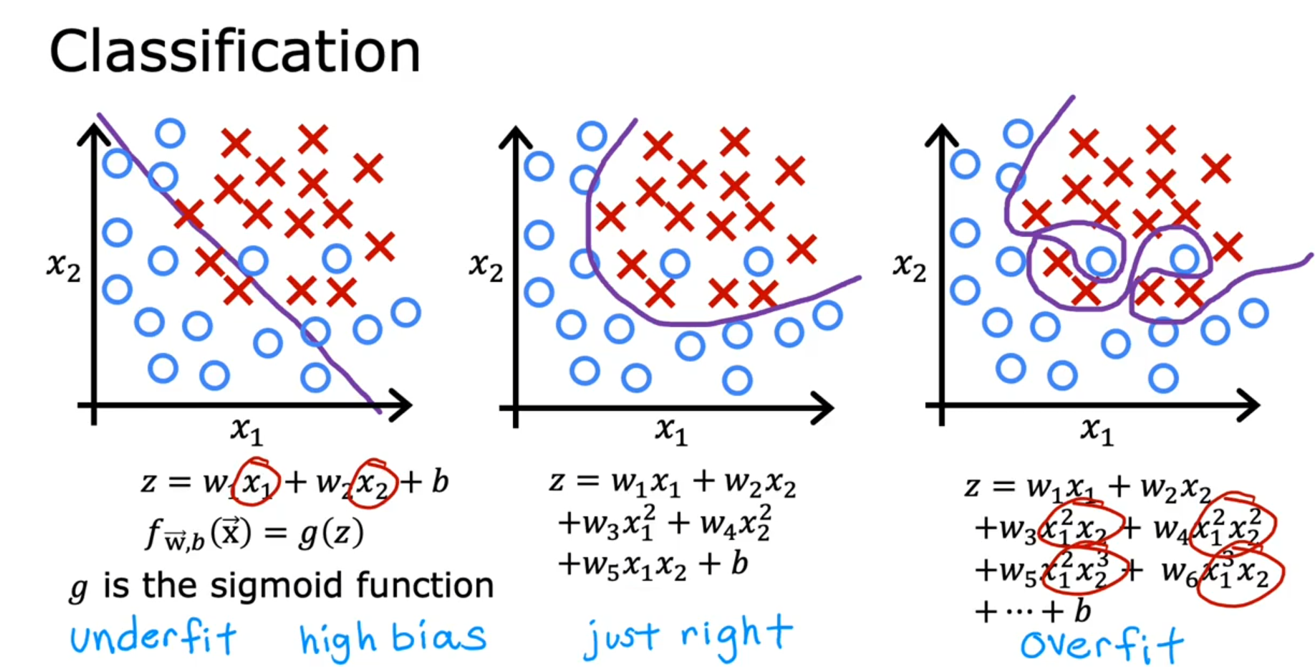
所谓过拟合,就是当模型参数太多,导致训练出的模型和当前训练集拟合太好,而出现新数据时却出现很大误差,也就是模型泛化能力差。
所谓正则化(Regularization),就是正则化代价函数,尽可能减小参数的影响(相当于减少参数),使模型没有对训练数据进行过拟合,从而增加泛化能力。如下图所示:
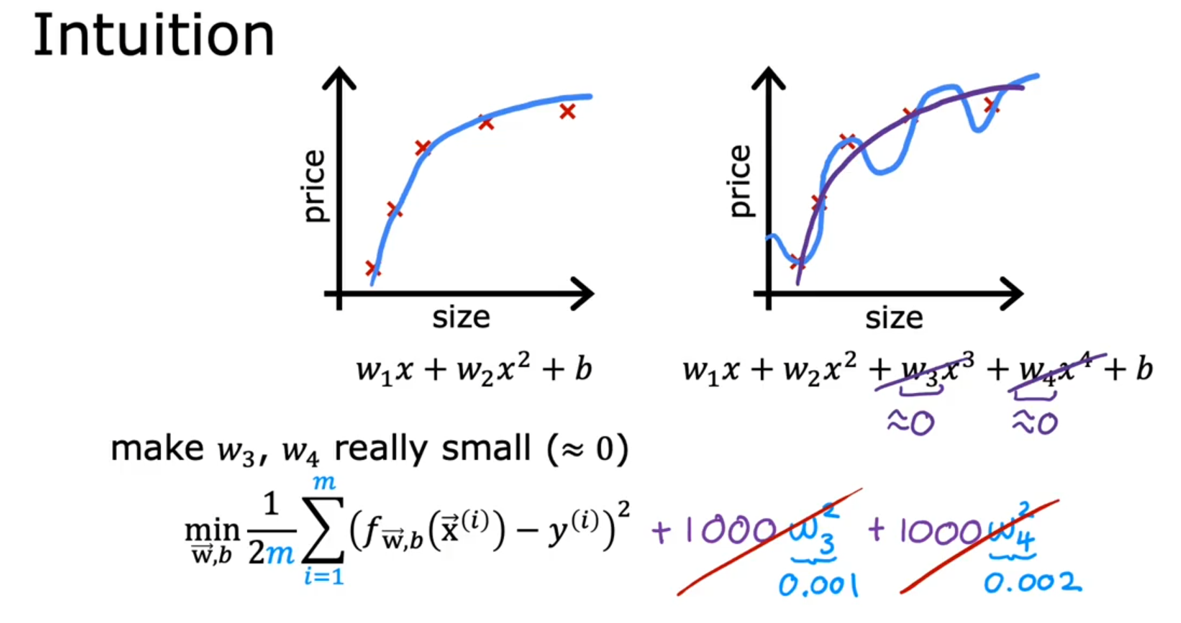
知道了正则化的原因和思想后,下面看看,这个正则化代价函数的过程,在线性回归和逻辑回归中是具体如何实现的。
3.2:线性回归中的正则化
可以看到,通过对代价函数进行正则化:加入正则化项,对代价函数进行正则化
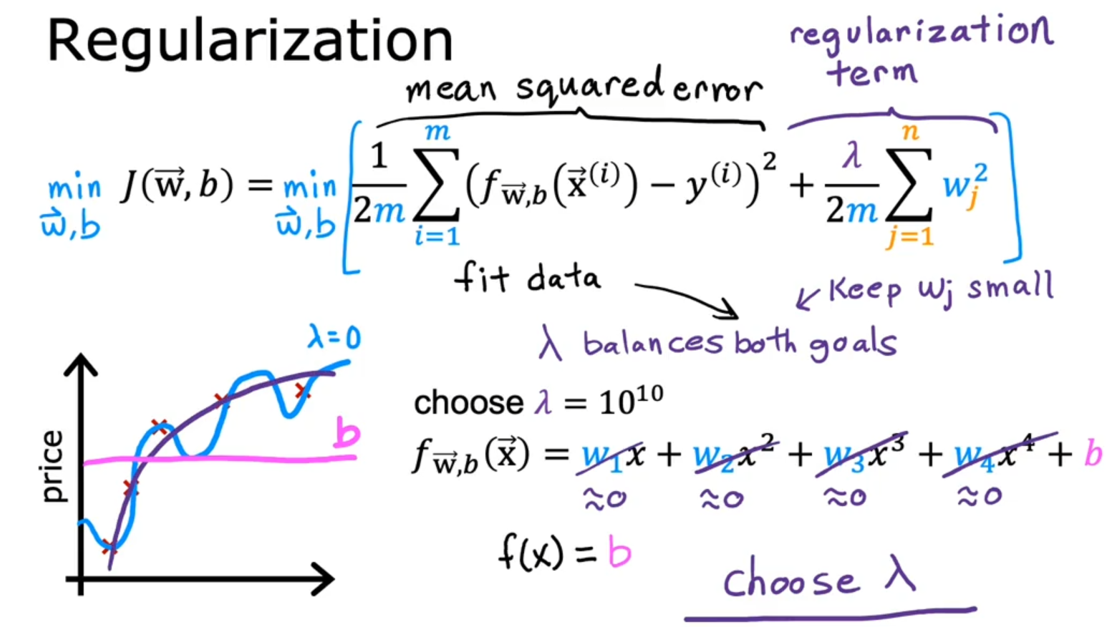
下面看看这个正则化项是如何在梯度下降过程中起作用的:
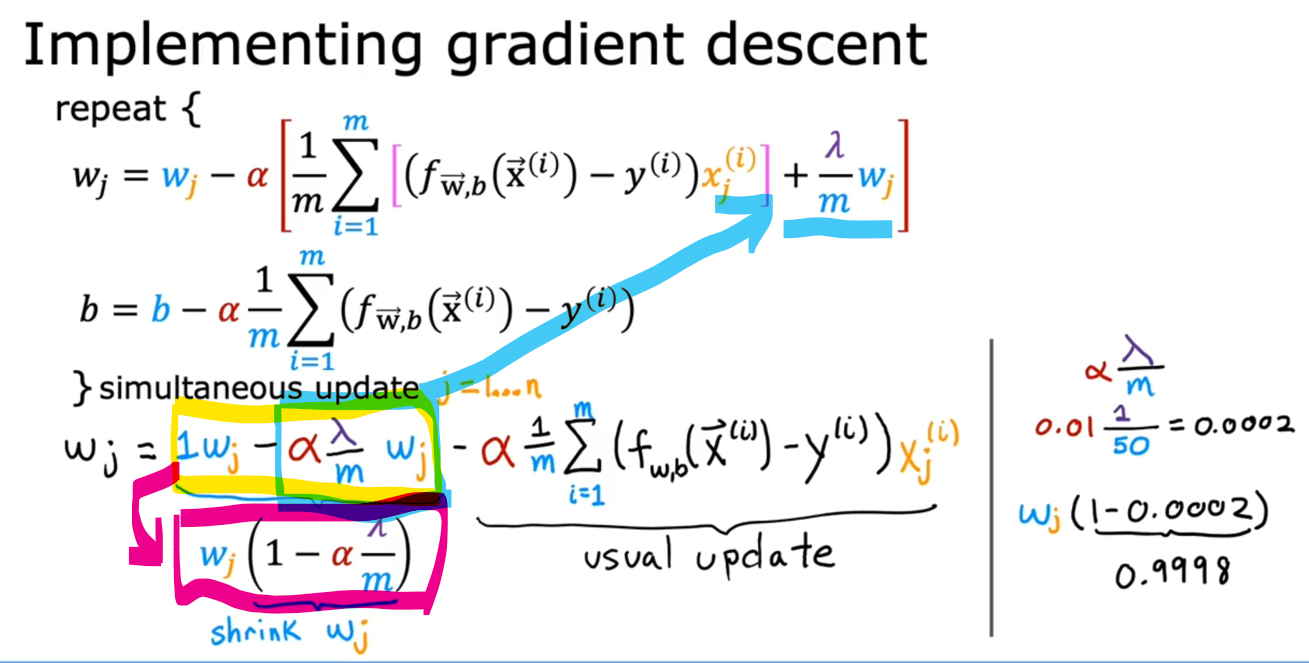
上图可以看到,加入正则化项之后,会减小w,也就是减小w的影响,从而使模型不那么过拟合!
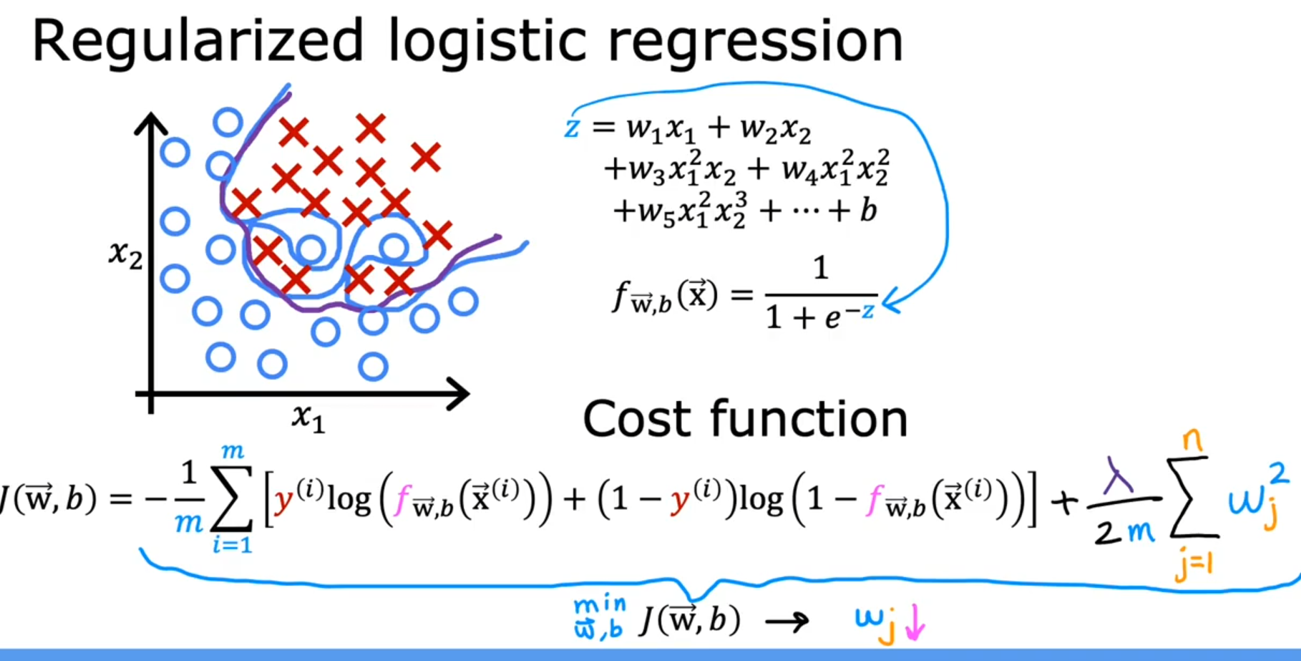
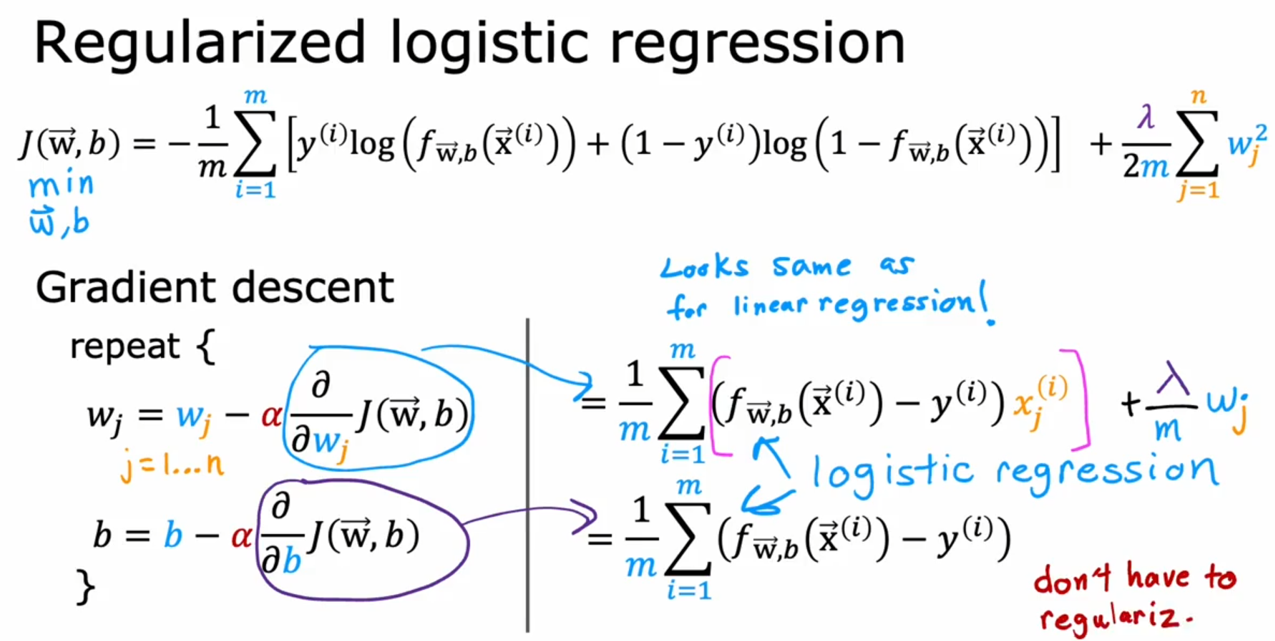
3.3:逻辑回归中的正则化
步骤和思想与线性回归中的正则化完全一致
🦄下期预告:高级的机器学习的监督学习算法:神经网络





