【数据结构】Splay树（伸展树）

前置知识

二叉树

就是一个长这样的树，树中每个结点都有一个父结点（除了根结点没有父结点）和最多两个子结点，每个结点的左儿子一定比它小，右儿子一定比它大。
在这里插入图片描述
这棵树的先序遍历很容易知道就是：1 2 3 4 5 6 7 （根左右）
我们还可以从另一个角度理解先序遍历：把整棵树映射到 x 轴上，也就是把它压扁也就是这样：

先序遍历从左到右读出来就可以了

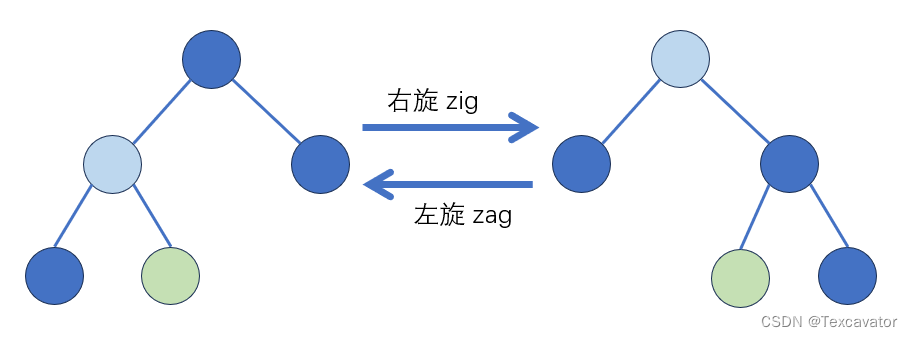
单旋：左旋 / 右旋

口诀：左旋拎右左挂右，右旋拎左右挂左

图示：
在这里插入图片描述
code

void zig(int &p) // 右旋 (以p为根)
{int q = tr[p].l; // 根结点的左儿子，我们要把这个结点旋到根结点tr[p].l = tr[q].r;tr[q].r = p;p = q;pushup(tr[p].r), pushup(p);
}void zag(int &p) // 左旋 (以p为根)
{int q = tr[p].r; // 根结点的右儿子，我们要把这个结点旋到根结点tr[p].r = tr[q].l;tr[q].l = p;p = q;pushup(tr[p].l), pushup(p);
}

主要内容

结构体

后续代码全部基于下方结构体定义：

struct Node
{int l, r; // 分别表示左右儿子int val; // 表示当前点权值int size; // 表示以当前点为根的子树中有多少结点int cnt; // 表示有多少与当前点权值一样的数
}spl[maxn];

双旋（伸展）

假设我们每次都要将最下层的结点挪到根结点，对于三个结点的组合，有以下四种双旋方式，其中对于一字型的调整也叫做同构调整，对于之字形的调整叫做异构调整

zig-zig

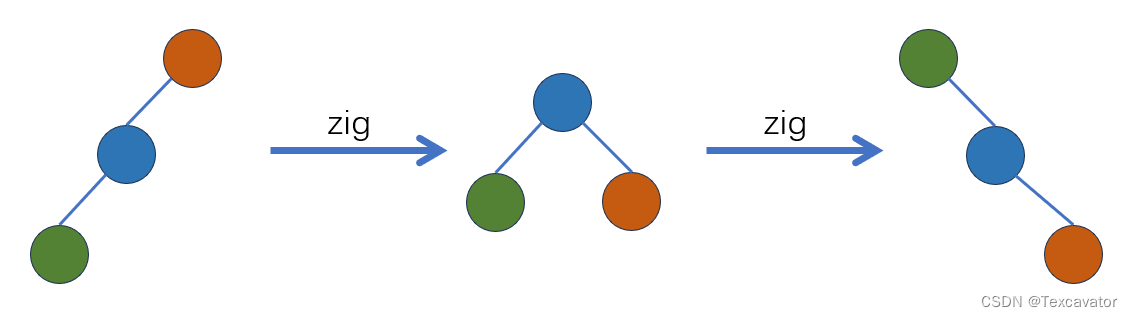
在这里插入图片描述
对于这样的一字型，且向左边，我们采用两次右旋

zag-zag

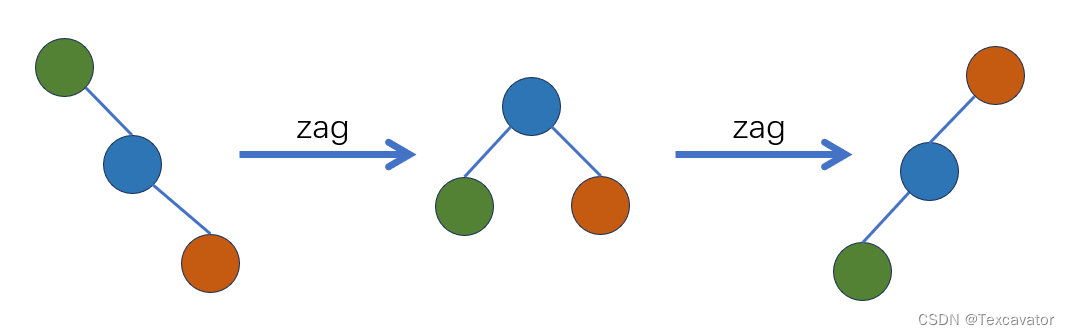
在这里插入图片描述
对于这样的一字型，且向右边，我们采用两次左旋

zig-zag

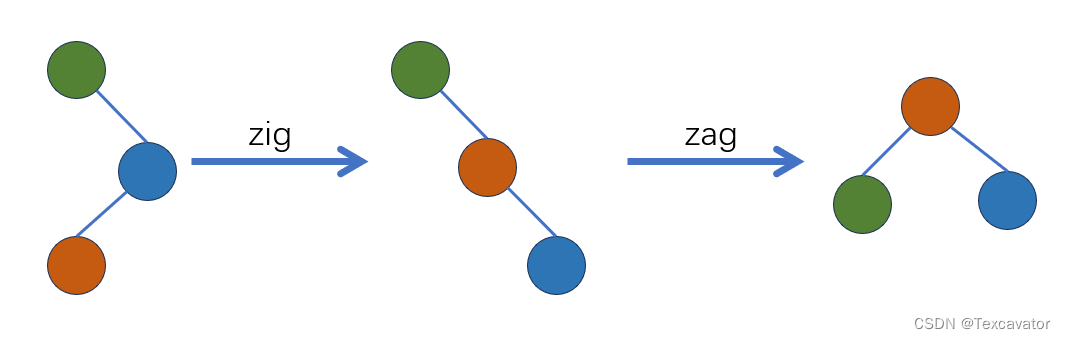
在这里插入图片描述
对于这样的之字形，大于号形状，我们采用先对蓝色结点右旋，再对根结点左旋

zag-zig

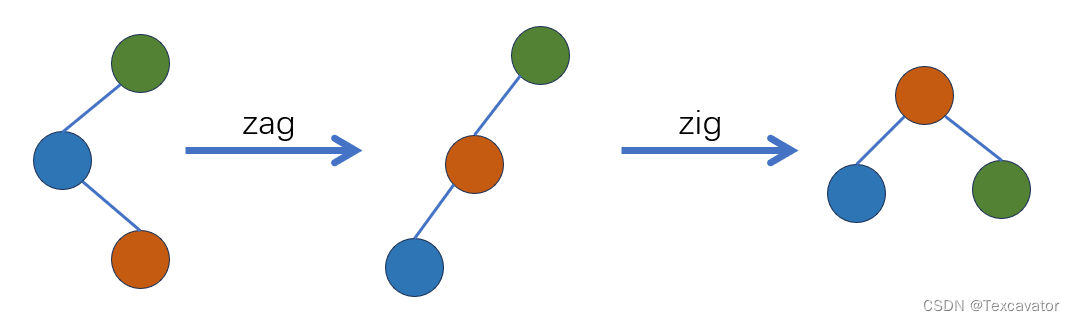
在这里插入图片描述
对于这样的之字形，小于号形状，我们采用先对蓝色结点左旋，再对根结点右旋

code

void splaying(int x, int &y) // 把x挪到y的位置
{if (x == y) return;int &l = spl[y].l, &r = spl[y].r;if (x == l) zig(y); // x是y的左儿子else if (x == r) zag(y); // x是y的右儿子else // x至少要经过一次双旋才能到y{if (spl[x].val < spl[y].val) // x在y的左子树{if (spl[x].val < spl[l].val) // x在y的左儿子的左子树{splaying(x, spl[l].l); // 先把x旋转到y的左儿子的左儿子zig(y), zig(y); // 进行zig-zig双旋}else // x在y的左儿子的右子树{splaying(x, spl[l].r); // 先把x旋转到y的左儿子的右儿子zag(l), zig(y); // 进行zag-zig双旋}}else // x在y的右子树{if (spl[x].val < spl[r].val) // x在y的右儿子的左子树{splaying(x, spl[r].l); // 先把x旋转到y的右儿子的左儿子zig(r), zag(y); // 进行zig-zag双旋}else // x在y的右儿子的右子树{splaying(x, spl[r].r); // 先把x旋转到y的右儿子的右儿子zag(y), zag(y); // 进行zag-zag双旋}}}
}

插入 insert

递归找到该插入的位置，然后再把这个结点splaying到根结点

void insert(int &p, int val)
{if (!p) // 如果p结点不存在，创建结点并将其splaying到根结点getnode(p, val), splaying(p, root);else if (val < spl[p].val) insert(spl[p].l, val); // 要插入的值比当前结点值小，递归进入左子树else if (val > spl[p].val) insert(spl[p].r, val); // 要插入的值比当前结点值大，递归进入右子树else spl[p].size ++ , spl[p].cnt ++ , splaying(p, root); // 当前平衡树中已有该值，直接更新
}

删除 remove

先把要删除的结点splaying到根结点，然后：

如果根结点没有右子树（也就是没有后继（也就是根结点就是最大值）），那么直接删掉即可，也就是把根结点变成当前根结点的左儿子
如果根结点有右子树（也就是有后继），就递归找到根结点的后继（也就是从根结点开始，先往右走一步，再一直往左走），把后继splaying到根结点的右儿子，此时这个后继一定没有左子树（因为有左子树，后继就会是左子树里的值），我们要删去根结点，直接让根结点的右儿子的左儿子指向根结点的左儿子即可

code

void remove(int p, int val) // 当前结点为p，要删去值为val的结点
{if (spl[p].val == val){splaying(p, root); // 先把要删去的结点splaying到根结点if (spl[p].cnt > 1) spl[p].cnt -- , spl[p].size -- ; // 要删去的数在树中存在不止一个，更新cnt和size即可else if (!spl[root].r) root = spl[root].l; // 当前结点没有后继else // 当前结点有后继{// 找到当前结点后继qint q = spl[root].r;while (spl[q].l) q = spl[q].l;splaying(q, spl[root].r); // 把后继splaying到根结点的右儿子spl[spl[root].r].l = spl[root].l; // 后继的左儿子变为根结点的左儿子root = spl[root].r; // 根结点变为后继pushup(root);}}else if (val < spl[p].val) remove(spl[p].l, val); // 待删结点在当前结点左子树else remove(spl[p].r, val); // 待删结点在当前结点右子树
}

根据值查询排名

int getrank_bykey(int val)
{int p = root, rank = 1;while (p){if (spl[p].val == val) // 找到值为val的结点{rank += spl[spl[p].l].size;splaying(p, root); // 把当前结点splaying到根结点break;}if (val <= spl[p].val) p = spl[p].l; // 待求结点在当前结点的左子树else // 待求结点在当前结点的右子树{rank += spl[spl[p].l].size + spl[p].cnt; // 加上左子树和本身的结点数p = spl[p].r;}}return rank;
}

根据排名查询值

int getkey_byrank(int rank)
{int p = root;while (p){if (spl[spl[p].l].size < rank && rank <= spl[spl[p].l].size + spl[p].cnt) // 在这个范围内就是当前结点{splaying(p, root); // 把当前结点splaying到根结点break;}else if (rank <= spl[spl[p].l].size) p = spl[p].l; // 待求结点在当前结点的左子树else // 待求结点在当前结点的右子树{rank -= spl[spl[p].l].size + spl[p].cnt; // 减去左子树和本身的结点数p = spl[p].r;}}return spl[p].val;
}

完整代码模板

#include <bits/stdc++.h>using namespace std;const int maxn = 100010;struct Node
{int l, r; // 分别表示左右儿子int val; // 表示当前点权值int size; // 表示以当前点为根的子树中有多少结点int cnt; // 表示有多少与当前点权值一样的数
}spl[maxn];int idx; // 记录结点编号开到几
int root; // 记录当前根结点编号是几void getnode(int &p, int val) // 建立一个编号为p 权值是val的结点
{if (!p) p = ++ idx; // 给新结点编号spl[p].size = spl[p].cnt = 1; // 初始化size和cntspl[p].val = val; // 赋初值
}void pushup(int u)
{spl[u].size = spl[spl[u].l].size + spl[spl[u].r].size + spl[u].cnt;
}void zig(int &p) // 右旋 (以p为根)
{int q = spl[p].l;spl[p].l = spl[q].r;spl[q].r = p;p = q;pushup(spl[p].r), pushup(p);
}void zag(int &p) // 左旋 (以p为根)
{int q = spl[p].r;spl[p].r = spl[q].l;spl[q].l = p;p = q;pushup(spl[p].l), pushup(p);
}void splaying(int x, int &y) // 把x挪到y的位置
{if (x == y) return;int &l = spl[y].l, &r = spl[y].r;if (x == l) zig(y); // x是y的左儿子else if (x == r) zag(y); // x是y的右儿子else // x至少要经过一次双旋才能到y{if (spl[x].val < spl[y].val) // x在y的左子树{if (spl[x].val < spl[l].val) // x在y的左儿子的左子树{splaying(x, spl[l].l); // 先把x旋转到y的左儿子的左儿子zig(y), zig(y); // 进行zig-zig双旋}else // x在y的左儿子的右子树{splaying(x, spl[l].r); // 先把x旋转到y的左儿子的右儿子zag(l), zig(y); // 进行zag-zig双旋}}else // x在y的右子树{if (spl[x].val < spl[r].val) // x在y的右儿子的左子树{splaying(x, spl[r].l); // 先把x旋转到y的右儿子的左儿子zig(r), zag(y); // 进行zig-zag双旋}else // x在y的右儿子的右子树{splaying(x, spl[r].r); // 先把x旋转到y的右儿子的右儿子zag(y), zag(y); // 进行zag-zag双旋}}}
}void insert(int &p, int val)
{if (!p) // 如果p结点不存在，创建结点并将其splaying到根结点getnode(p, val), splaying(p, root);else if (val < spl[p].val) insert(spl[p].l, val); // 要插入的值比当前结点值小，递归进入左子树else if (val > spl[p].val) insert(spl[p].r, val); // 要插入的值比当前结点值大，递归进入右子树else spl[p].size ++ , spl[p].cnt ++ , splaying(p, root); // 当前平衡树中已有该值，直接更新
}void remove(int p, int val) // 当前结点为p，要删去值为val的结点
{if (spl[p].val == val){splaying(p, root); // 先把要删去的结点splaying到根结点if (spl[p].cnt > 1) spl[p].cnt -- , spl[p].size -- ; // 要删去的数在树中存在不止一个，更新cnt和size即可else if (!spl[root].r) root = spl[root].l; // 当前结点没有后继else // 当前结点有后继{// 找到当前结点后继qint q = spl[root].r;while (spl[q].l) q = spl[q].l;splaying(q, spl[root].r); // 把后继splaying到根结点的右儿子spl[spl[root].r].l = spl[root].l; // 后继的左儿子变为根结点的左儿子root = spl[root].r; // 根结点变为后继pushup(root);}}else if (val < spl[p].val) remove(spl[p].l, val); // 待删结点在当前结点左子树else remove(spl[p].r, val); // 待删结点在当前结点右子树
}int getrank_bykey(int val)
{int p = root, rank = 1;while (p){if (spl[p].val == val) // 找到值为val的结点{rank += spl[spl[p].l].size;splaying(p, root); // 把当前结点splaying到根结点break;}if (val <= spl[p].val) p = spl[p].l; // 待求结点在当前结点的左子树else // 待求结点在当前结点的右子树{rank += spl[spl[p].l].size + spl[p].cnt; // 加上左子树和本身的结点数p = spl[p].r;}}return rank;
}int getkey_byrank(int rank)
{int p = root;while (p){if (spl[spl[p].l].size < rank && rank <= spl[spl[p].l].size + spl[p].cnt) // 在这个范围内就是当前结点{splaying(p, root); // 把当前结点splaying到根结点break;}else if (rank <= spl[spl[p].l].size) p = spl[p].l; // 待求结点在当前结点的左子树else // 待求结点在当前结点的右子树{rank -= spl[spl[p].l].size + spl[p].cnt; // 减去左子树和本身的结点数p = spl[p].r;}}return spl[p].val;
}