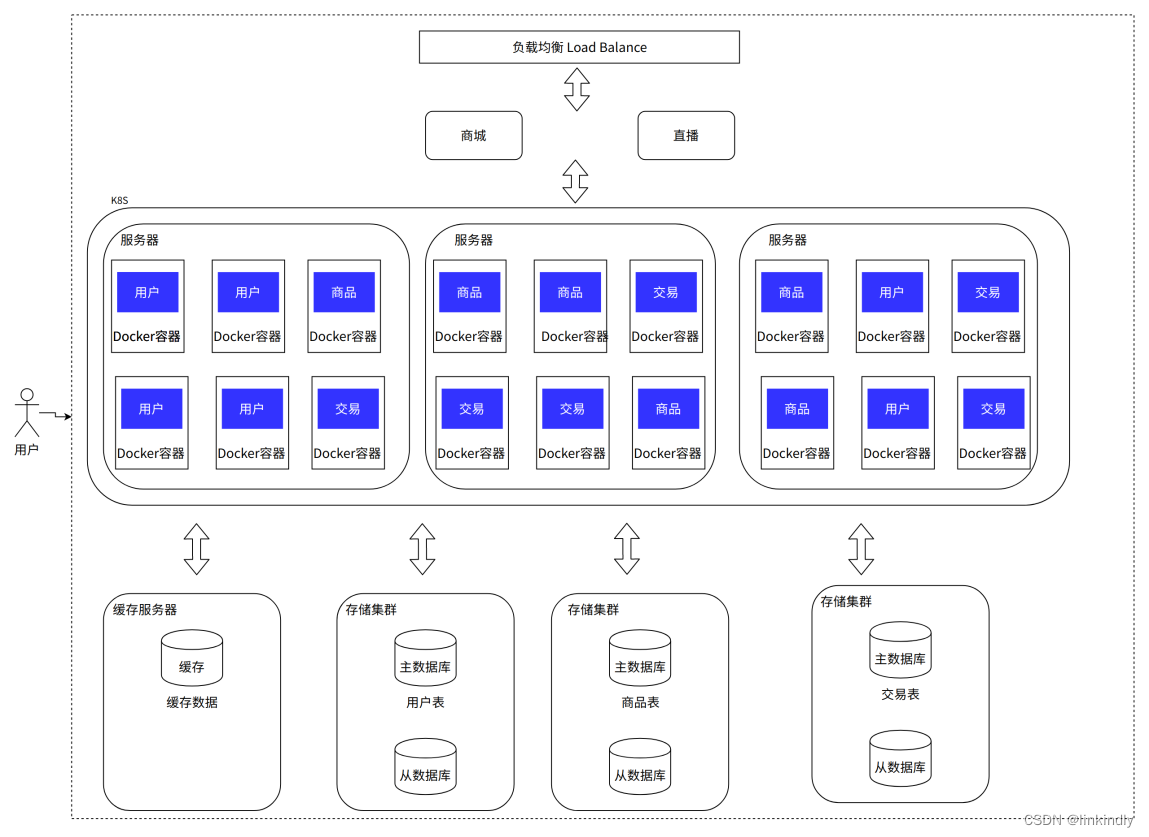
文章目录
- 平面上点到直线的距离
平面上点到直线的距离
- 设坐标平面上有点 P ( x 1 , y 1 ) P(x_1,y_1) P(x1,y1)和直线 l : A x + B y + C = 0 l:Ax+By+C=0 l:Ax+By+C=0, A , B A,B A,B不全为0
- 点 P P P到直线 l l l的的距离的算法推导如下
- 作直线 m m m通过点 P ( x 1 , y 1 ) P(x_1,y_1) P(x1,y1),并且和直线 l l l垂直,设垂足为 P 0 ( x 0 , y 0 ) P_0(x_0,y_0) P0(x0,y0)
- 令: d 2 = ∣ P 0 P 1 ∣ 2 = ( x 1 − x 0 ) 2 + ( y 1 − y 0 ) 2 d^2=|P_0P_1|^2=(x_1-x_0)^2+(y_1-y_0)^2 d2=∣P0P1∣2=(x1−x0)2+(y1−y0)2
(0),所求的就是 d d d - 由直线垂直对应的方程关系可设直线 P P 0 PP_0 PP0的方程为 B x − A y + D = 0 B{x}-Ay+D=0 Bx−Ay+D=0
(1)- 因为 P P P在 P P 0 PP_0 PP0上,从而 B x 0 − A y 0 + D = 0 Bx_0-Ay_0+D=0 Bx0−Ay0+D=0
(1-1) - 两式相减,得 B ( x − x 0 ) − A ( y − y 0 ) = 0 B(x-x_0)-A(y-y_0)=0 B(x−x0)−A(y−y0)=0
(1-2) - 将 P 0 P_0 P0代入到(1-2),得 B ( x 0 − x 1 ) − A ( y 0 − y 1 ) B(x_0-x_1)-A(y_0-y_1) B(x0−x1)−A(y0−y1)=0
(1-3)
- 因为 P P P在 P P 0 PP_0 PP0上,从而 B x 0 − A y 0 + D = 0 Bx_0-Ay_0+D=0 Bx0−Ay0+D=0
- 又因为 P 0 P_0 P0还在 l l l上,从而 A x 0 + B y 0 + C = 0 Ax_0+By_0+C=0 Ax0+By0+C=0,从而 C = − A x 0 − B y 0 C=-Ax_0-By_0 C=−Ax0−By0
(1-4), - 构造 t = A x 1 + B y 1 + C t=Ax_1+By_1+C t=Ax1+By1+C,由(1-4),得 t = A x 1 + B y 1 − A x 0 − B y 0 t=Ax_1+By_1-Ax_0-By_0 t=Ax1+By1−Ax0−By0= A ( x 1 − x 0 ) + B ( y 1 − y 0 ) A(x_1-x_0)+B(y_1-y_0) A(x1−x0)+B(y1−y0)
(1-5),即 A ( x 1 − x 0 ) + B ( y 1 − y 0 ) = t A(x_1-x_0)+B(y_1-y_0)=t A(x1−x0)+B(y1−y0)=t(1-6)- 将(1-3)两边平方加上(1-6)两边平方,整理得
- ( A 2 + B 2 ) [ ( x 1 − x 0 ) 2 + ( y − y 0 ) 2 ] (A^2+B^2)[(x_1-x_0)^2+(y-y_0)^2] (A2+B2)[(x1−x0)2+(y−y0)2]= t 2 t^2 t2
(1-7);代入(0),得 ( A 2 + B 2 ) d 2 (A^2+B^2)d^2 (A2+B2)d2= t 2 t^2 t2 - 所以 d 2 d^2 d2= t 2 ( A 2 + B 2 ) \frac{t^2}{(A^2+B^2)} (A2+B2)t2
- d d d= ∣ t ∣ A 2 + B 2 \frac{|t|}{\sqrt{A^2+B^2}} A2+B2∣t∣= ∣ A x 1 + B y 1 + C ∣ A 2 + B 2 \frac{|Ax_1+By_1+C|}{\sqrt{A^2+B^2}} A2+B2∣Ax1+By1+C∣
(1-8)