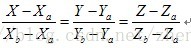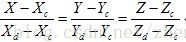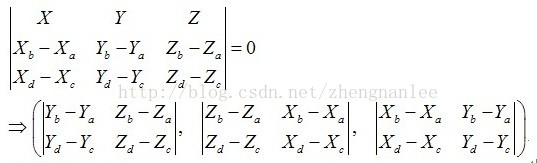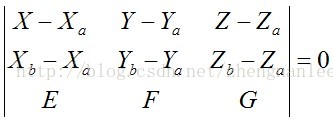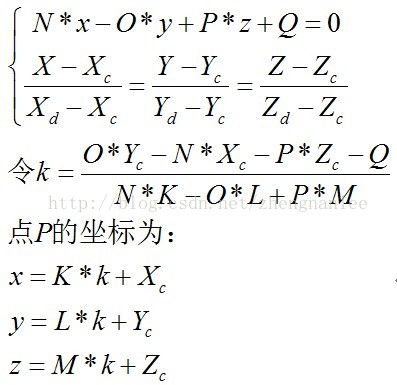额有必要写写了~

公式啊。

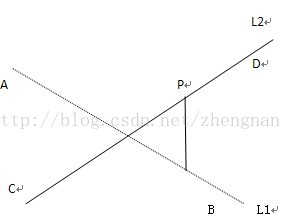
两条直线：

构造方程：

求出公垂线向量：

记公垂线和l1形成的平面为alpha，下面求它：

令：

联立：

不难得到如下代码：

#include <iostream> #include <math.h> #include <iomanip> #include <algorithm> #define eps 1e-8 #define zero(x) (((x)>0?(x):-(x))<eps) struct point3{ double x, y, z; }; struct line3{ point3 a, b; }; struct plane3{ point3 a, b, c; }; using namespace std; point3 xmult(point3 u, point3 v) {     point3 ret;     ret.x = u.y*v.z - v.y*u.z;     ret.y = u.z*v.x - u.x*v.z;     ret.z = u.x*v.y - u.y*v.x;     return ret; } point3 subt(point3 u, point3 v) {     point3 ret;     ret.x = u.x - v.x;     ret.y = u.y - v.y;     ret.z = u.z - v.z;     return ret; } double dmult(point3 u, point3 v) {     return u.x*v.x + u.y*v.y + u.z*v.z; } double vlen(point3 p) {     return sqrt(p.x*p.x + p.y*p.y + p.z*p.z); } double linetoline(line3 u, line3 v) {     point3 n = xmult(subt(u.a, u.b), subt(v.a, v.b));     return fabs(dmult(subt(u.a, v.a), n)) / vlen(n); } double linetoline(point3 u1, point3 u2, point3 v1, point3 v2) {     point3 n = xmult(subt(u1, u2), subt(v1, v2));     return fabs(dmult(subt(u1, v1), n)) / vlen(n); } int main() {     int T;     cin >> T;     while (T--)     {         point3 a, b, c, d;         cin >> c.x >> c.y >> c.z >> d.x >> d.y >> d.z >> a.x >> a.y >> a.z >> b.x >> b.y >> b.z;         cout << fixed << setprecision(6) << linetoline(a, b, c, d) << endl;         double H = b.x - a.x, I = b.y - a.y, J = b.z - a.z;         double K = d.x - c.x, L = d.y - c.y, M = d.z - c.z;         double N = H * I * L - I * I * K - J * J * K + H * J * M;         double O = H * H * L - H * I * K - I * J * M + J * J * L;         double P = H * J * K - H * H * M - I * I * M + I *J * L;         double Q = -a.x * N + a.y * O - a.z * P;         double k = (O * c.y - N * c.x - P * c.z - Q) / (N * K - O * L + P * M);         cout << fixed << setprecision(6) << K * k + c.x << ' ' << L * k + c.y << ' ' << M * k + c.z << ' ';         swap(a, c);         swap(b, d);         H = b.x - a.x, I = b.y - a.y, J = b.z - a.z;         K = d.x - c.x, L = d.y - c.y, M = d.z - c.z;         N = H * I * L - I * I * K - J * J * K + H * J * M;         O = H * H * L - H * I * K - I * J * M + J * J * L;         P = H * J * K - H * H * M - I * I * M + I *J * L;         Q = -a.x * N + a.y * O - a.z * P;         k = (O * c.y - N * c.x - P * c.z - Q) / (N * K - O * L + P * M);         cout << fixed << setprecision(6) << K * k + c.x << ' ' << L * k + c.y << ' ' << M * k + c.z << endl;     } }