一、前言

        本文基于LSTM模型，使用torch搭载，本文输入的为多变量，输出结果为生猪价格。数据结构如下图所示：

        由于数据本身版权原因，因此仅公布部分数据。

 二、输入特征选择

        明确猪肉价格的伙伴应当知道猪周期的道理。以下是本人浅略简介：

猪肉价格是农产品市场的晴雨表，猪肉是百姓菜篮子中的关键食物。生猪与粮食价格的重要性可以从每年的中央一号文件窥见一斑。对于中国来说，中国人吃掉了全球一半的猪肉。对中国上下五千年的“家文化“中的”家“咬文嚼字可以发现，家里面就是一只猪，足以体现猪在中国国民生活中的重要地位和猪的文化色彩。从量上说，2010年以来，中国猪肉的人均占有量都在45公斤以上。2019年，虽然受到非洲猪瘟疫情的影响，国内猪肉产量有加有较大幅度的下降，但仍然达到了4255万吨。而猪肉价格的波动，从消费者的角度来说，猪肉价格上涨将降低人民生活水平，抑制猪肉消费、抑制其他消费，抬高物价水平；从生产者的角度来说，由于我国养猪户大多都是农村散养农民，经济理性程度低，当猪肉价格上涨，农户养猪利润增大，便会扩大生猪养殖，进而造成供给增加，然而随着平衡点的越过，猪肉市场供大于求，又会促使猪肉价格下降，农户养猪热情降低，因而减少生猪供给，进而猪肉价格抬高，农民开始养殖猪肉，这就造成了猪肉价格的周期性波动。而该周期性波动就被称为猪周期。

         “猪周期“与猪肉价格影响因素：猪周期是猪肉价格随着市场经济呈现周期性波动的一种经济现象，具体成因已然陈述，而其具体周期为：

 

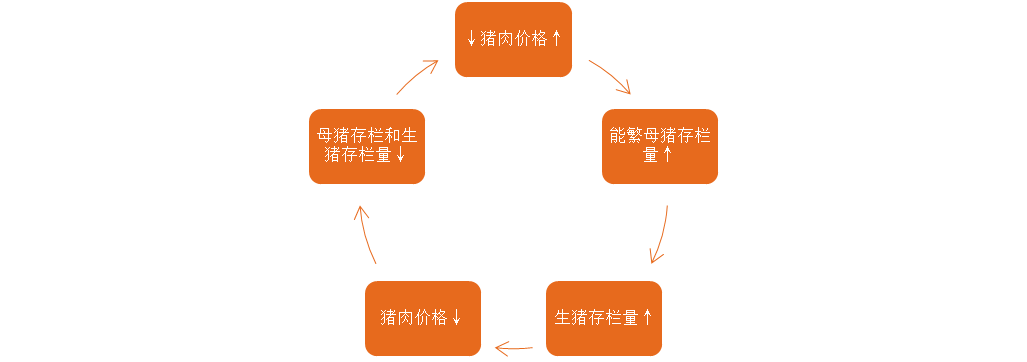
        由于猪肉价格与生猪价格的波动高度一致，因此猪肉价格可以使用生猪价格进行代理。由上述所言，在生猪价格的波动分析中需要重点关注猪周期的影响。猪周期是猪肉价格波动的关键原因之一，而生猪的养殖还和养殖成本、市场需求等高度相关，如生猪的食物价格、替代品价格以及宏观经济环境等因素等的影响。

>因此，在选择输入变量时，应当充分考虑到猪周期的影响，选择滞后多少期的变量非常关键。

>本文选择的是相关系数与互信息的选择方法。

 三、时序图绘制

        左图为时间序列图，右图为STL分解图：

 

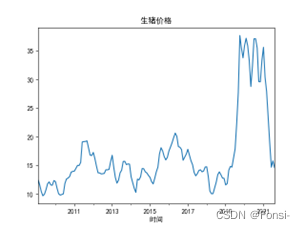
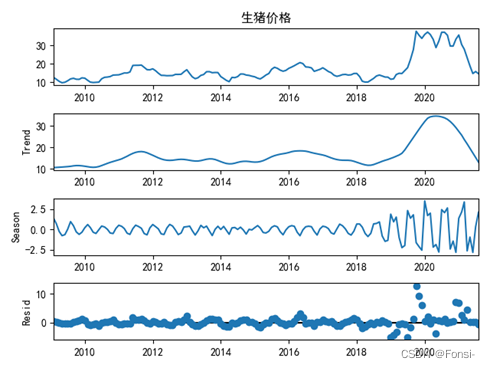
在STL分解法中，周期大致也是小周期6个月，大周期4年左右。通过对生猪价格时间序列的分解，直接证明了猪周期的存在。同时也不难发现，生猪价格波动的季节效应也明显，这符合客观认知。

四、自相关分析

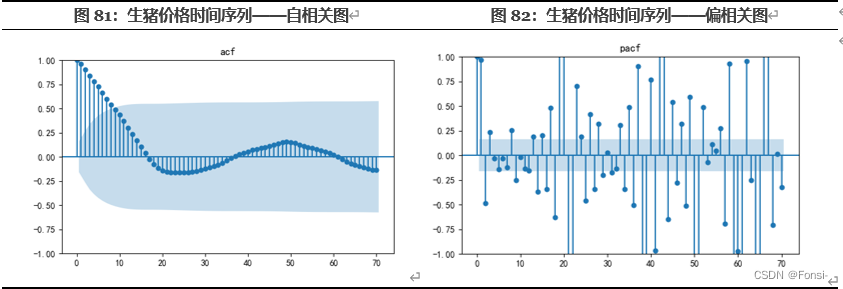
自相关图显示，生猪价格具有非常强烈的短期相关性，但事实上延长到18期左右也依然有一定的相关性。质言之，短期相关与长期相关都非常强烈。而从偏相关图可以看出，生猪价格也呈现出了非常明显的周期性和季节性。一个大周期大致持续2年左右，期间也有较多的小周期和季节效应的影响。这进一步佐证了猪周期的存在。而这也充分说明了在生猪价格的分析中，有必要纳入生猪价格滞后期的影响。此外，通过ADF检验，该时间序列为平稳时间序列

五、LSTM模型

 LSTM，全称Long Short Term Memory(长短期记忆)，是一种特殊的递归神经网络。这种网络与一般的前馈神经网络不同，LSTM可以利用时间序列对输入进行分析；质言之，当使用前馈神经网络时，神经网络会认为我们t时刻输入的内容与t+1输入的内容完全无关。为了运用到时间维度上信息，人们设计了递归神经网络RNN，一个简单的递归神经网络可以用这种方式表示：、

 在图中，xt是在t时刻的输入信息，ht是在t时刻的输入信息，我们可以看到神经元A会递归的调用自身并且将t-1时刻的信息传递给t时刻。

而上述简单的递归神经网络存在硬伤，即长期依赖问题：递归神经网络只能处理我们需要较接近的上下文情况。而LSTM从设计之初就是用于解决一般RNN中普遍存在的长期以来问题。使用LSTM可以有效的传递和表达长时间序列中的信息并且不会导致长时间前的有用信息被忽略。此外还可以解决RNN中的梯度爆炸问题。

 在这里，我们可以看到A在 t−1 时刻的输出值 ht−1 被复制到了 t 时刻，与 t 时刻的输入 xt 整合后经过一个带权重和偏置的tanh函数后形成输出，并继续将数据复制到 t+1 时刻，以此循环往复。但与上图朴素的RNN相比，单个LSTM单元拥有更加复杂的内部结构和输入输出：

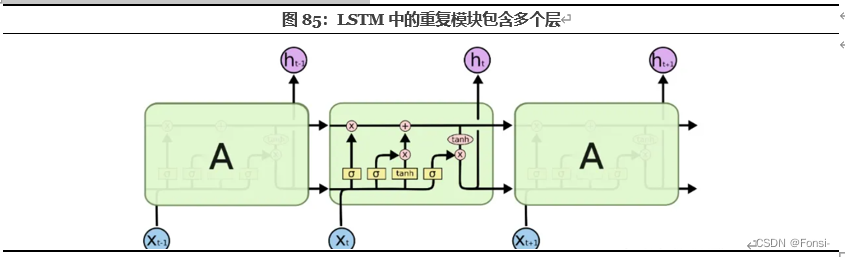
上述表述借鉴于知乎、CSDN其他博主表述，侵删。

因此，LSTM非常适合用来作时间序列的预测分析，在多特征时间序列预测中也能展现出较快的运行速度和拟合能力。、

六、预测数据

结合生猪价格时间序列的自相关分析，我认为12期多步纳入的期间甚至不能涵盖一个大型猪周期，学习的效果一定不佳。最终的拟合情况正如我所预料，因此，我认为有必要作至少18期的多步预测，而为了减少对2019年-2021年上半年异常数据的学习，减少极端值的影响，我认为还需要再多纳入一个季节效应，因此，最终选择21步的多步预测。

 

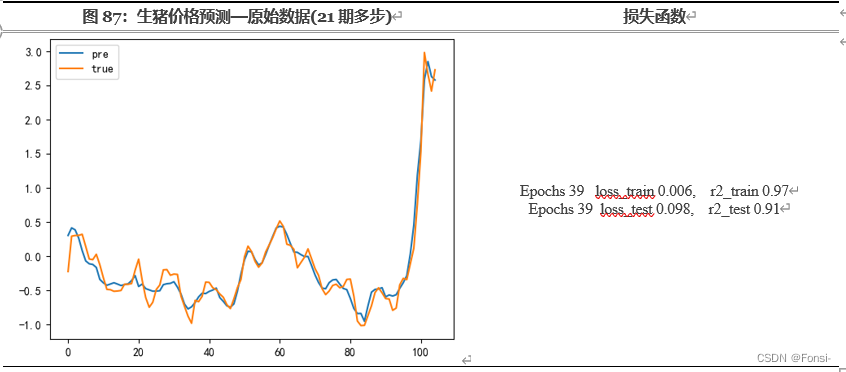
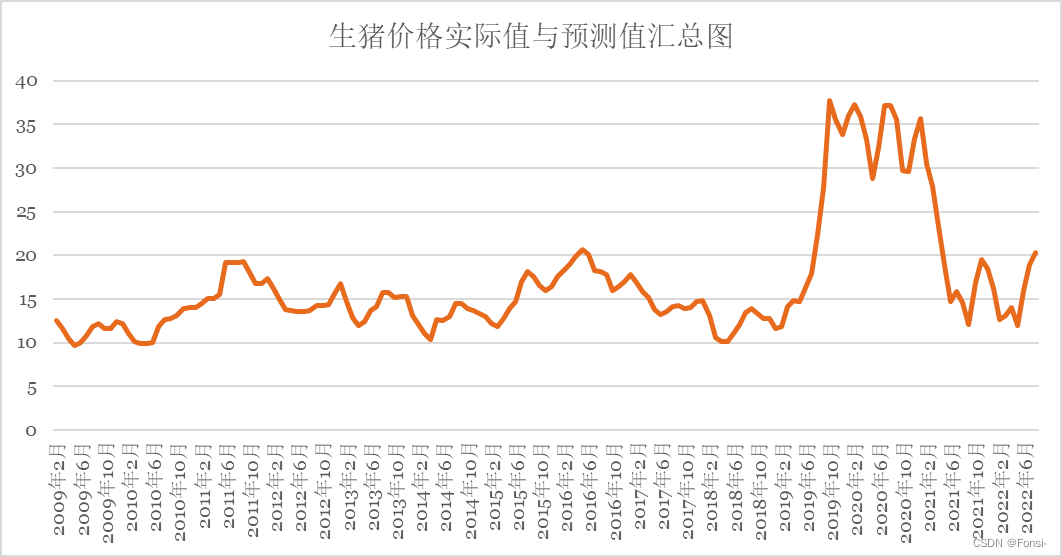
七、SHAP可视化

1.神经网络的主要缺陷在于其是一种黑匣子，并不像决策树、线性回归那样知道每一个变量的权重或者说系数。但是SHAP值（Shapley Additive explanations）即沙普利加和解释，是将输出值归因到每一个特征的shapely的值上。可以通过每一个特征的SHAP值来衡量特征对最终输出值的影响。具体阐述本人才疏学浅，参考知乎代码博主进行解释。

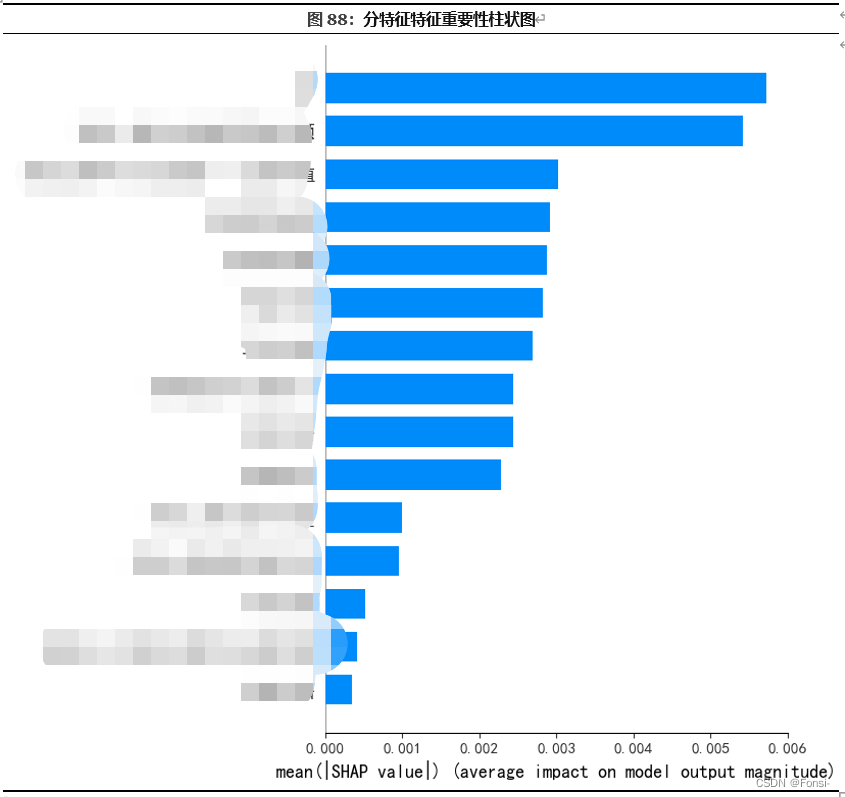
 2. 特征数值对生猪价格预测值的影响可视化

以上图像为每个样本绘制其每个特征的SHAP值，这可以更好地理解整体模式，并允许发现预测异常值。每一行代表一个特征，横坐标为SHAP值。一个点代表一个样本，颜色表示特征值(红色高，蓝色低)。

八、部分代码

        仅列示部分核心步骤，请使用Jupyter完成，没有一步到位的。完整代码若需要请私信。

import torch
from torch import nn,optim
import torch.utils.data as Data
import torch.nn.functional as F
import seaborn as sns
import numpy as np
import pandas as pd
import os ,re ,random
import matplotlib.pylab as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
import sklearn.preprocessing as preprocessing
from sklearn.model_selection import train_test_split
from sklearn.metrics import f1_score,recall_score,precision_score,roc_curve,roc_auc_score,accuracy_score,confusion_matrix,r2_score
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import brier_score_loss
from sklearn.calibration import calibration_curve
from sklearn import metrics
import scipydf = pd.read_excel('生猪价格数据集-LSTM.xlsx',sheet_name="0")
df.head(148)df = df.iloc[:,1:]plt.plot(df['生猪价格'])df = pd.read_excel('生猪价格数据集-LSTM.xlsx',sheet_name="0")
df = df.iloc[:,1:]
n=21s1 = StandardScaler()
df = s1.fit_transform(df)
x = []
y = []
for i in range(len(df)-n-n):x.append(df[i:i+n])y.append(df[i+n:i+n+n,0])x = np.array(x)
y = np.array(y)
# x = x.reshape(-1,15,n)
X_train,X_test,Y_train ,Y_test= train_test_split(x,y,test_size = 0.2,random_state=1)
X_train = torch.tensor(X_train,dtype = torch.float)
X_test = torch.tensor(X_test,dtype = torch.float)
Y_train  = torch.tensor(Y_train,dtype = torch.float)
Y_test  = torch.tensor(Y_test,dtype = torch.float)train_loader = Data.DataLoader(dataset=Data.TensorDataset(X_train, Y_train),  # 封装进Data.TensorDataset()类的数据，可以为任意维度batch_size=13,  # 每块的大小shuffle=False,  drop_last =True, #丢弃最后一组数据num_workers=0,  # 多进程（multiprocess）来读数据
)
test_loader = Data.DataLoader(dataset=Data.TensorDataset(X_test, Y_test),  # 封装进Data.TensorDataset()类的数据，可以为任意维度batch_size=13,  # 每块的大小shuffle=False,  drop_last =True, num_workers=0,  # 多进程（multiprocess）来读数据
)
Y_test = Y_test.detach().numpy()
print(Y_test)
Y_train = Y_train.detach().numpy()class LSTM(nn.Module):def __init__(self, P,input_size, output_size,w, hidden_layer_size=50):""":param input_size: 输入数据的维度:param hidden_layer_size:隐层的数目:param output_size: 输出的个数"""super().__init__()
#         self.li1 = nn.Sequential(
#             self.lstm(input_x, hidden_cell)#         )self.hidden_layer_size = hidden_layer_sizeself.lstm = nn.LSTM(input_size, hidden_layer_size,num_layers=2,bidirectional =True,dropout=0.3,batch_first=True)self.sigmoid = nn.Sigmoid()self.linear1 = nn.Linear(hidden_layer_size*2, output_size)self.linear2 = nn.Linear(hidden_layer_size*2, hidden_layer_size*2)self.dropout = nn.Dropout(p=P)self.relu = nn.ReLU()self.ww = wdef forward(self, input_x):torch.manual_seed(1)input_x = input_x.reshape(-1,15,n)input_x = self.dropout(input_x)lstm_out, (h_n, h_c) = self.lstm(input_x)
#         print(lstm_out.shape)alpha = F.softmax(self.linear2(lstm_out),dim=1)
#         print(alpha.shape)lstm_out = lstm_out*alphalstm_out = torch.sum(lstm_out,1)linear_out = self.linear1(lstm_out.view(len(input_x), -1))  return linear_outmodel = LSTM(p,input_size,output_size,hidden_size)
loss_function = nn.MSELoss()  # loss
optimizer = torch.optim.Adam(model.parameters(), lr=l)  # 优化器
scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=9, gamma=0.95)
result = {}
result['train-mse'] = []
result['train-mape']= []
result['train-loss']= []
result['train-r2']= []
result['test-mse']= []
result['test-mape']= []
result['test-loss']= []
result['test-r2']= []
R2 = 0
for epochs in range(Epochs):loss_mean_train = 0loss_mean_test = 0r2_train = 0r2_test = 0model.train()for data_l in train_loader:seq, labels = data_loptimizer.zero_grad()y_pred = model(seq)labels = torch.squeeze(labels)single_loss = loss_function(y_pred, labels)loss_mean_train += single_loss.item()single_loss.backward()optimizer.step()scheduler.step()model.eval()y_predict = model(X_train).detach().numpy()
#     mse1 = np.sum((Y_train- y_predict) ** 2) / len(Y_train)mape1 = (sum(abs((y_predict - Y_train)/(Y_train+1)))/len(Y_train))*100mape1 = sum(mape1)/len(mape1)r2_train = r2_score(y_predict,Y_train)y_predict = model(X_test)single_loss_test = loss_function(y_predict, torch.squeeze(torch.tensor(Y_test,dtype = torch.float))).item()y_predict = y_predict.detach().numpy()
#     mse2 = np.sum((Y_test - y_predict) ** 2) / len(Y_test)mape2 = (sum(abs((y_predict - Y_test)/(Y_test+1)))/len(Y_test))*100mape2 = sum(mape2)/len(mape2)r2_test = r2_score(y_predict,Y_test)#     result['train-mse'].append(mse1)
#     result['test-mse'].append(mse2)result['train-mape'].append(mape1)result['test-mape'].append(mape2)result['train-r2'].append(r2_train)result['test-r2'].append(r2_test)result['train-loss'].append(loss_mean_train/len(train_loader))result['test-loss'].append(single_loss_test)print('Epochs',epochs,'loss_train',loss_mean_train/len(train_loader),'r2_train',r2_train)print('Epochs',epochs,'loss_test',single_loss_test,'r2_test',r2_test)if R2 < r2_test:R2 =r2_testtorch.save(model, 'model_lstm3.pth')print('已更新保存模型')