出一期比较尴尬的博客——有关线代教材的课后题总结~
之所以说尴尬,主要有两个主要原因:这本科教版第三版的教材,整体看起来并不是那么舒服,甚至被我们的老师吐槽过,更好地选择时同济版的那本紫书——我们学校的新生这两年全改用了;另一方面,说实话对于学校的考试来说,这些题目练练手还是能保证80分的,再不济及格是肯定没问题,但是对于考研来说,比较降维打击——尤其是数学一。相对来说,课后题分(一)、(二)两个部分,(二)中的题目较难,但尴尬的是其实不是很对标考研。。。所以,本帖的宗旨是整理一下可能出现的题型种类,并选用一些偏容易得例题,大家可以围绕题型目录,自己找一些更难的题~
考研数学一考纲:
第一章:行列式
考试内容:
行列式的概念和基本性质 行列式按行(列)展开定理
考试要求:
1.了解行列式的概念,掌握行列式的性质.
2.会应用行列式的性质和行列式按行(列)展开定理计算行列式.
第二章:矩阵
考试内容:
矩阵的概念 矩阵的线性运算 矩阵的乘法 方阵的幂 方阵乘积的行列式 矩阵的转置 逆矩阵的概念和性质矩阵可逆的充分必要条件 伴随矩阵 矩阵的初等变换初等矩阵矩阵的秩矩阵等价 分块矩阵及其运算
考试要求:
1.理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵和反对称矩阵以及它们的性质.
2.掌握矩阵的线性运算、乘法、转置以及它们的运算规律,了解方阵的幂与方阵乘积的行列式的性质.
3.理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可逆的充分必要条件,理解伴随矩阵的概念,会用伴随矩阵求逆矩阵.
4.理解矩阵的初等变换的概念,了解初等矩阵的性质和矩阵等价的概念,理解矩阵的秩的概念,掌握用初等变换求矩阵的秩和逆矩阵的方法.
5.了解分块矩阵及其运算.
第三章:向量
考试内容:
向量的概念 向量的线性组合和线性表示 向量组的线性相关与线性无关 向量组的极大线性无关组等价向量组 向量组的秩 向量组的秩与矩阵的秩之间的关系 向量空间以及相关概念 n维向量空间的基变换和坐标变换 过渡矩阵 向量的内积 线性无关向量组的正交规范化方法 规范正交基 正交矩阵及其性质
考试要求:
1.理解n维向量、向量的线性组合与线性表示的概念.
2.理解向量组线性相关、线性无关的概念,掌握向量组线性相关、线性无关的有关性质及判别法.
3.理解向量组的极大线性无关组和向量组的秩的概念,会求向量组的极大线性无关组及秩.
4.理解向量组等价的概念,理解矩阵的秩与其行(列)向量组的秩之间的关系
5.了解n维向量空间、子空间、基底、维数、坐标等概念.
6.了解基变换和坐标变换公式,会求过渡矩阵.
7.了解内积的概念,掌握线性无关向量组正交规范化的施密特(Schmidt)方法.
8.了解规范正交基、正交矩阵的概念以及它们的性质.
第四章:线性方程组
考试内容:
线性方程组的克莱姆(Cramer)法则齐次线性方程组有非零解的充分必要条件非齐次线性方程组有解的充分必要条件 线性方程组解的性质和解的结构 齐次线性方程组的基础解系和通解 解空间 非齐次线性方程组的通解
考试要求
l.会用克莱姆法则.
2.理解齐次线性方程组有非零解的充分必要条件及非齐次线性方程组有解的充分必要条件.
3.理解齐次线性方程组的基础解系、通解及解空间的概念,掌握齐次线性方程组的基础解系和通解的求法.
4.理解非齐次线性方程组解的结构及通解的概念.
5.掌握用初等行变换求解线性方程组的方法.
第五章:矩阵的特征值及特征向量
考试内容:
矩阵的特征值和特征向量的概念、性质 相似变换、相似矩阵的概念及性质 矩阵可相似对角化的充分必要条件及相似对角矩阵 实对称矩阵的特征值、特征向量及相似对角矩阵
考试要求:
1.理解矩阵的特征值和特征向量的概念及性质,会求矩阵的特征值和特征向量.
2.理解相似矩阵的概念、性质及矩阵可相似对角化的充分必要条件,掌握将矩阵化为相似对角矩阵的方法.
3.掌握实对称矩阵的特征值和特征向量的性质.
第六章:二次型
考试内容:
二次型及其矩阵表示 合同变换与合同矩阵二次型的秩 惯性定理 二次型的标准形和规范形 用正交变换和配方法化二次型为标准形 二次型及其矩阵的正定性
考试要求:
1.掌握二次型及其矩阵表示,了解二次型秩的概念,了解合同变化和合同矩阵的概念 了解二次型的标准形、规范形的概念以及惯性定理.
2.掌握用正交变换化二次型为标准形的方法,会用配方法化二次型为标准形.
3.理解正定二次型、正定矩阵的概念,并掌握其判别法

- 行列式定义的理解
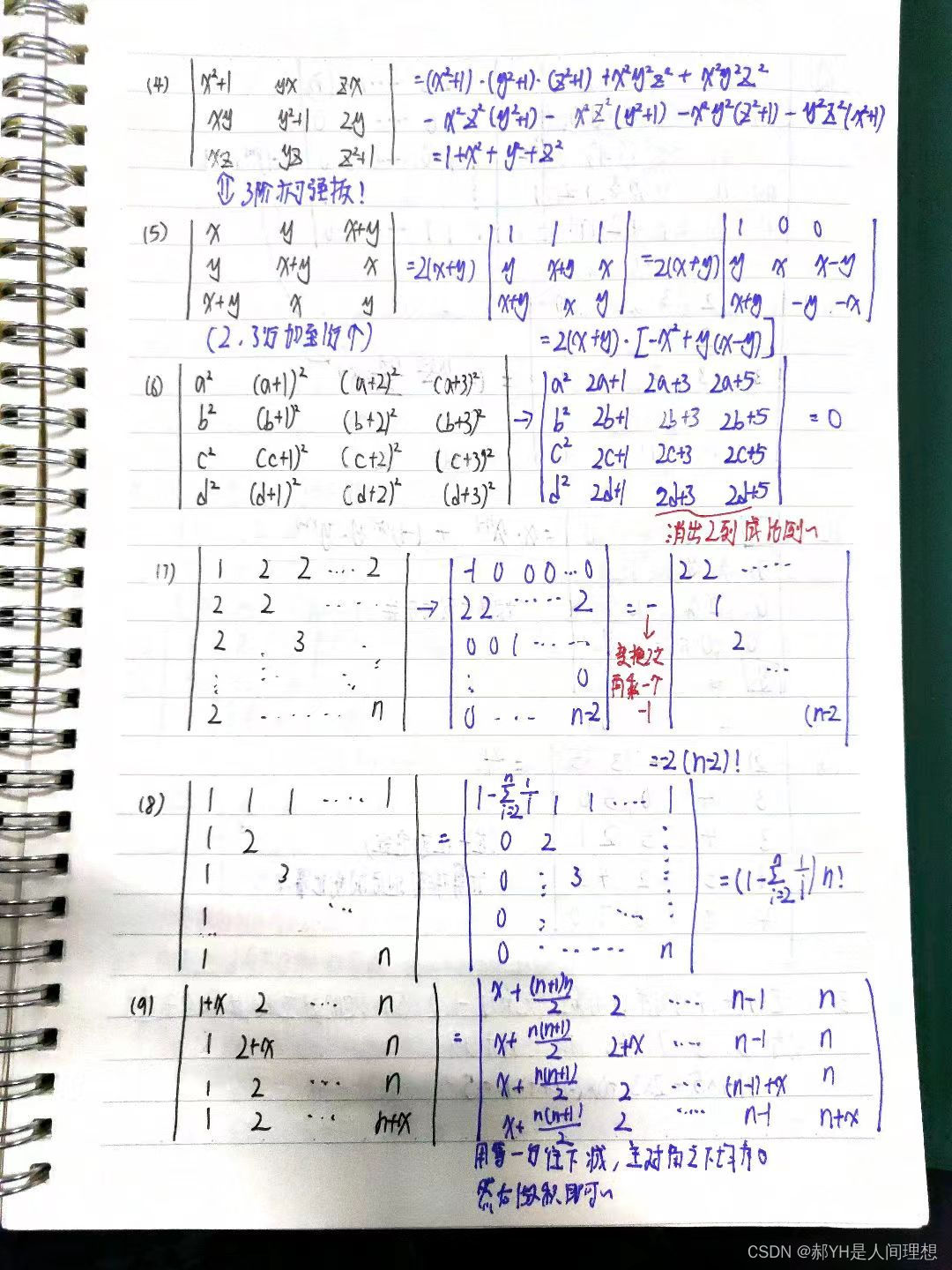
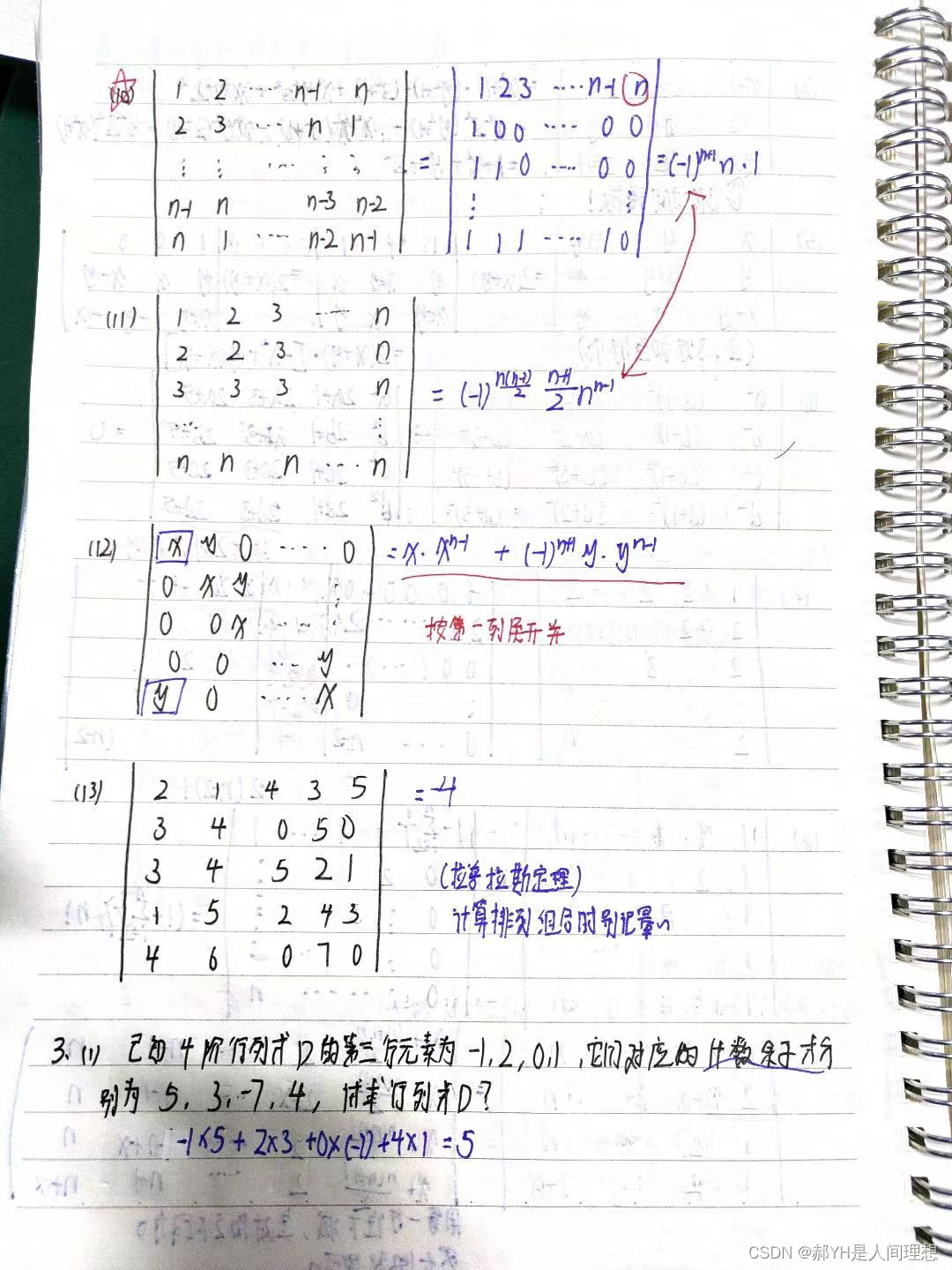
- 行列式的算数运算
- 与代数余子式有关性质有关的题
- 克拉默法则相关
- 行列式的证明题
- 矩阵的基本运算
- 矩阵的基本性质
- 计算逆矩阵
- 分块矩阵的相关性质
- 计算矩阵的秩
- 计算向量or写出线性组合
- 有关线性表示的题
- 讨论线性相关性
- 线性相关的证明题
- 求解向量的极大线性无关组
- 用基础解系表示方程组的解
- 讨论解的存在情况
- 求解矩阵的特征值和特征向量
- 有关特征值的相关证明
- 矩阵的幂运算
- 矩阵相似
- 正交矩阵
- 写出二次型的矩阵
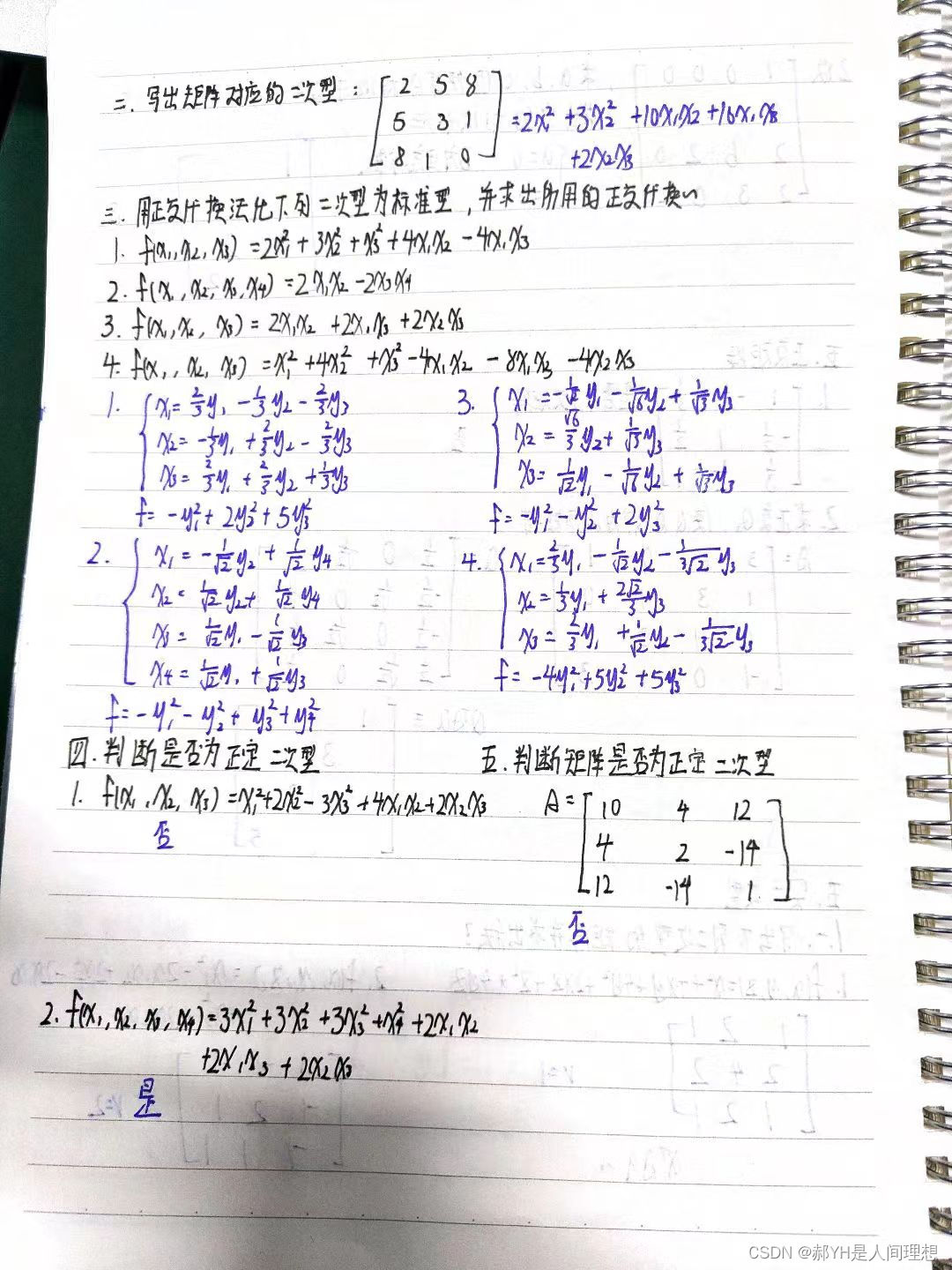
- 写出矩阵对应的二次型
- 用正交代换法化下列二次型为标准型,并求出所用的正交代换
- 判断是否为正定二次型
- 判断矩阵是否为正定二次型