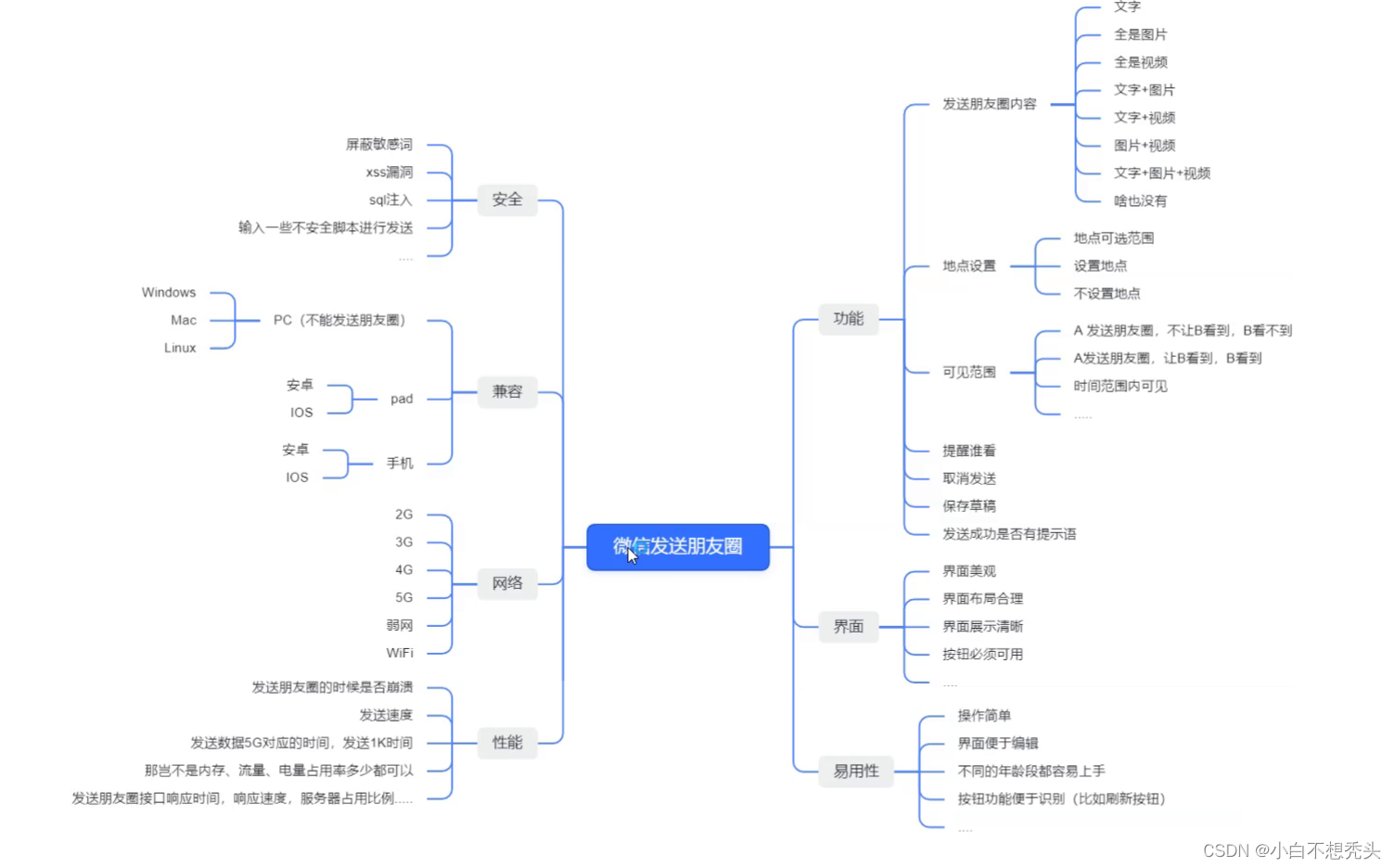
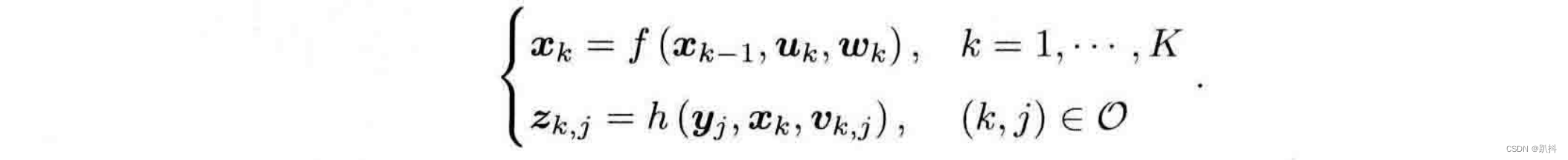162.寻找峰值
方法一:寻找最大值
题目保证了nums[i]≠nums[i+1],所以数组nums中最大值两侧的元素一定严格小于最大值本身,因此最大值所在的位置就是一个可行的峰值位置
class Solution {public int findPeakElement(int[] nums) {int idx = 0;for(int i=0;i<nums.length;i++){if(nums[i] > nums[idx]){idx = i;}}return idx;}
}
方法二:使二分查找优化迭代爬坡
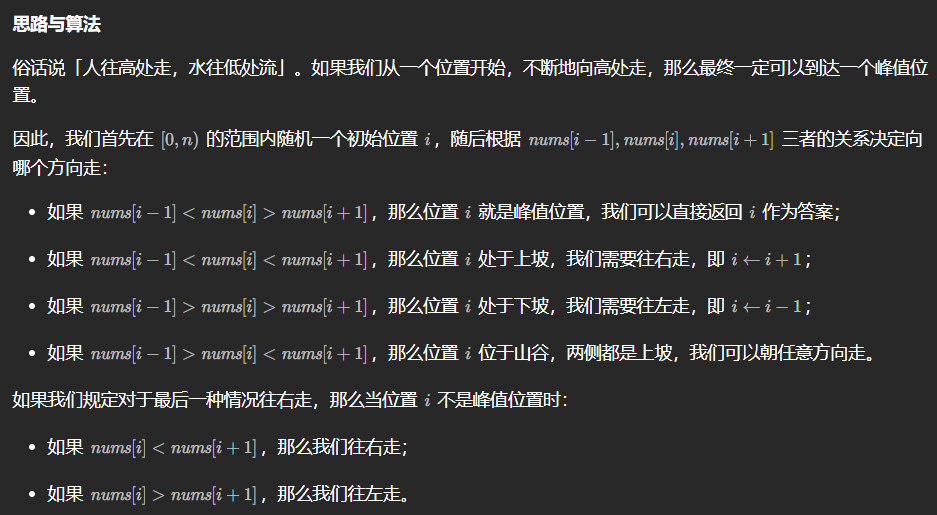

class Solution {public int findPeakElement(int[] nums) {int n = nums.length;int left = 0,right = n - 1,ans = -1;while(left <= right){int mid = (left + right) / 2;if(compare(nums,mid - 1,mid) < 0 && compare(nums,mid,mid + 1) > 0){ans = mid;break;}if(compare(nums,mid,mid + 1)< 0){left = mid + 1;}else{right = mid -1;}}return ans;}// 辅助函数,输入下标 i,返回一个二元组 (0/1, nums[i])// 方便处理 nums[-1] 以及 nums[n] 的边界情况public int[] get(int[] nums,int idx){if(idx == -1 || idx == nums.length){return new int[]{0,0};}return new int[]{1,nums[idx]};}public int compare(int[] nums,int idx1,int idx2){int[] num1 = get(nums,idx1);int[] num2 = get(nums,idx2);if(num1[0] != num2[0]){return num1[0] > num2[0] ? 1:-1;} if(num1[1] == num2[1]){return 0;}return num1[1] > num2[1] ? 1:-1;}
}
方法三:二分查找
- 在题目描述中出现了nums[-1]=nums[n]=-∞,就代表着只要数组中存在一个元素比相邻元素大,那么沿着它一定就可以找到一个峰值
- 根据上述结论,可以使用二分查找找到峰值
- 查找时,左指针l,右指针r,以其保持左右顺序为循环条件
- 根据右指针计算中间位置m,并比较m和m+1的值,如果m较大,则左侧存在峰值,r=m,如果m+1较大,则右侧存在峰值,l=m+1
class Solution {public int findPeakElement(int[] nums) {int left = 0, right = nums.length - 1;for (; left < right; ) {int mid = left + (right - left) / 2;if (nums[mid] > nums[mid + 1]) {right = mid;} else {left = mid + 1;}}return left;}
}