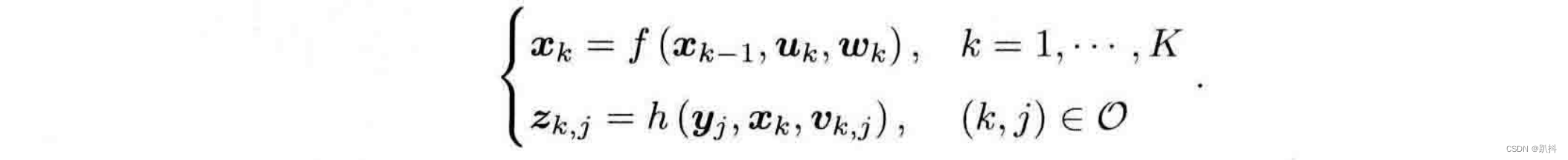积分上限函数

积分上限函数

news/2024/12/12 16:36:57/

定积分的形式

$\int_{a}^{b}f(x)dx$

a：积分下限

b：积分上限

定积分的值与积分变量无关

$\int_{a}^{b}f(x)dx = \int_{a}^{b}f(t)=dt$

积分上限函数的形式

$\varphi (x) = \int_{a}^{x}f(t)dt$

x：自变量

t：积分变量

积分上限是变量，积分下限是常数

定积分的几何意义

$\int_{a}^{b}f(x)dx$

$y=f(x),x =a,x=b$ x轴所围成面积

x轴以上面积为正

x轴以下面积为负

积分上限函数的几何意义

$\int_{a}^{x}f(x)dx$

a：是常数固定的

x：是自变量不断的变化的

左边界固定，右边界是不断移动的所围成的面积代数和。

积分上限函数求导法则

$\varphi(x) = \int_{a}^{x}f(x)dx \\ \varphi(x)^{'} = f(x)$

$\varphi(\omega(x)) = \int_{a}^{\omega(x)}f(t)dt \\ \varphi(\omega(x))^{'} = f(\omega(x))\cdot\omega(x)^{'}$ 复合函数链式求导法则

例题1

$f(x)$ 二阶可导， $f(0) = 0, f(0)^{'} = 1$ ,求 $\lim_{x \to 0} \frac{\int_{0}^{x}[f(t)\cdot t^2-t^3]dt}{x^4}$

上下都趋于0 可使用洛必达法则

利用积分上限函数求导法则求分子

$\lim_{x \to 0}\frac{f(x)\cdot x^2 - x^3}{4x^3} \\ \lim_{x \to 0}\frac{f(x)\cdot x^2}{4x^3} - \lim_{x \to 0}\frac{x^3}{4x^3} \\ \lim_{x \to 0}\frac{f(x)}{4(x)} - \frac{1}{4}$

因为 $f(x)$ 二阶可导，所以 $f(x)^{'}$ 连续

利用导数定义

$\frac{1}{4}\lim_{x \to 0} \frac{f(x) - f(0)}{x} = \frac{1}{4}f(0)^{'}$

所以结果为0

http://www.ppmy.cn/news/1212099.html

相关文章

【视觉SLAM十四讲学习笔记】第二讲——初识SLAM

【视觉SLAM十四讲学习笔记】第二讲——初识SLAM

专栏系列文章如下： 【视觉SLAM十四讲学习笔记】第一讲一个机器人，如果想要探索某一块区域，它至少需要知道两件事： 我在什么地方——定位周围环境是什么样——建图一方面需要明白自身的状态（即位置）&#…

阅读更多...

导师对学生学术论文的指导包括哪些方面，请详细展开说明

导师对学生学术论文的指导包括哪些方面，请详细展开说明

导师在指导学生学术论文时涉及多个方面，这些方面旨在帮助学生培养独立研究和学术写作的能力。以下是一些导师可能涉及的主要方面： 1.选题和课题确定： 导师会与学生讨论潜在的研究兴趣和方向，帮助学生选择一个既有研究价值又符合其…

阅读更多...

docker去掉sudo权限方法

docker去掉sudo权限方法

查看用户组及成员 sudo cat /etc/group | grep docker 可以添加docker组 sudo groupadd docker 添加用户到docker组 sudo gpasswd -a huangxiujie docker 增加读写权限 sudo chmod arw /var/run/docker.sock 重启docker sudo systemctl restart docker

阅读更多...

测试用例的设计方法（黑盒）

测试用例的设计方法（黑盒）

1.基于需求的设计方法比如针对网易邮箱进行测试：分为功能相关和非功能相关两大类但是这么设计的话，有无数多个测试用例，我们现在看到的只是一些大概的测试用例，要想设计具体的测试用例，需要用到下面测试用例的方法…

阅读更多...

建行广东江门分行：科技赋能，数据助力纠“四风”

建行广东江门分行：科技赋能，数据助力纠“四风”

为进一步深化落实中央八项规定精神，持续加大“四风”问题查处力度，建行驻江门市分行纪检组根据《广东省分行贯彻落实中央八项规定精神持之以恒纠治“四风”实施方案》（建粤党发〔2023〕1号）安排，对驻在市分行开展“四风…

阅读更多...

国际阿里云：无法访问ECS实例中的服务的排查方法！！！

国际阿里云：无法访问ECS实例中的服务的排查方法！！！

操作场景无法访问ECS实例中的服务可能有以下原因： 可能原因排查方案 ECS实例的安全组未开放相应端口检查ECS实例安全组规则 ECS实例中，该服务未启动/开启或服务对应端口未被监听检查服务状态及端口监听状态 ECS实例内防火墙设置错误检查ECS…

阅读更多...

前端 BUG 总结

前端 BUG 总结

文章目录 CSS 样式1、Chrome 89 版本期不再支持 /deep/，请勿使用嵌套 /deep/2、圆角按钮 button 点击后出现矩形框线3、怪异模式4、border 1 像素在手机上显示问题5、文本溢出问题 JavaScript 脚本1、移动端点击穿透2、使用parseInt时必须补全第二个参数 radix3、有…

阅读更多...

建行驻江门市分行纪检组以政治谈话压责任促发展

建行驻江门市分行纪检组以政治谈话压责任促发展

开展政治谈话，是加强“一把手”和领导班子监督、严肃党内政治生活、加强对党员领导干部日常教育管理的有效手段。为督促“一把手”和领导班子成员依法依规履行职责、行使权力，推动党中央重大决策部署以及建设银行总行、广东省分行党委的决策部署在本单…

阅读更多...

最新文章