💓博主CSDN主页:杭电码农-NEO💓
 
⏩专栏分类:C语言学习分享⏪
 
🚚代码仓库:NEO的学习日记🚚
 
🌹关注我🫵带你学习更多C语言知识
  🔝🔝

---

---

---

1. 前言🚩

本篇文章带给大家的内容有,整型在内存中的存储,大端小端的介绍与判断,和一些练习.从这篇文章开始,我们将进入C语言进阶知识的部分.

---

2. 整型在内存中的存储🚩

比如我们定义两个整型变量:

int a = 20;
int b = -10;

我们知道整型在内存中占四个字节的空间,在这之前我们先了解下面的概念

---

2.1 源码,反码,补码🏁

计算机中的整数有三种2进制表示方法，即原码、反码和补码。
三种表示方法均有符号位和数值位两部分，符号位都是用0表示“正”，用1表示“负”，而数值位正数的原、反、补码都相同。
负整数的三种表示方法各不相同。

• 源码:直接将数值按照正负数的形式翻译成二进制就可以得到原码。
• 反码:将原码的符号位不变，其他位依次按位取反就可以得到反码。
• 补码:反码+1就得到补码。

我们说正整数的源码,反码,补码都相同.并且对于整形来说：数据存放内存中其实存放的是补码。

这是因为在计算机系统中，数值一律用补码来表示和存储。原因在于，使用补码，可以将符号位和数值域统一处理；
同时，加法和减法也可以统一处理（CPU只有加法器）此外，补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路。

	int main()
{int num  = 20;//创建一个整型变量，叫 num，这时num向内存申请4个字节来存放数据//4个字节-32比特位//00000000000000000000000000010100-原码//00000000000000000000000000010100-反码//00000000000000000000000000010100-补码//正整数源反补相同int num2 = -10;////10000000000000000000000000001010 - 原码//11111111111111111111111111110101 - 反码//11111111111111111111111111110110 - 补码//return 0;
}

假设我们要将这两个数相加,我们试试用反码,和补码相加,哪个是正确的:

源码相加:

//0000000000000000000000010100  num
//1000000000000000000000001010  num2
//1000000000000000000000011110  30的源码

补码相加:

//000000000000000000000010100  num
//111111111111111111111110110  num2
//011111111111111111111110110  补码
//000000000000000000000001010  10的源码   

我们有看见用补码做加减法是刚好符合逻辑的.

我们再来看看 -10 在 vs2022 编译器上的内存存储:

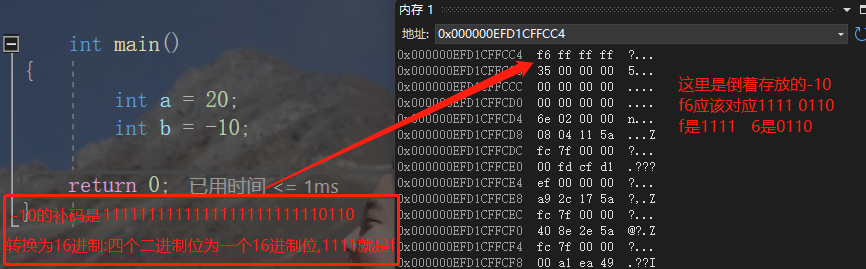
这里是倒着存放的数据,后面会讨论,现在我们暂且不看,但是我们能感受到实际上数据在内存中的存储是以补码的形式存储的

---

3. 大端和小端🚩

我们之前观察了补码在内存中的存储,我们发现有一点奇怪,为什么数据是倒着放的?这里我们用变量a来阐述这个问题

int a = 0x11223344;

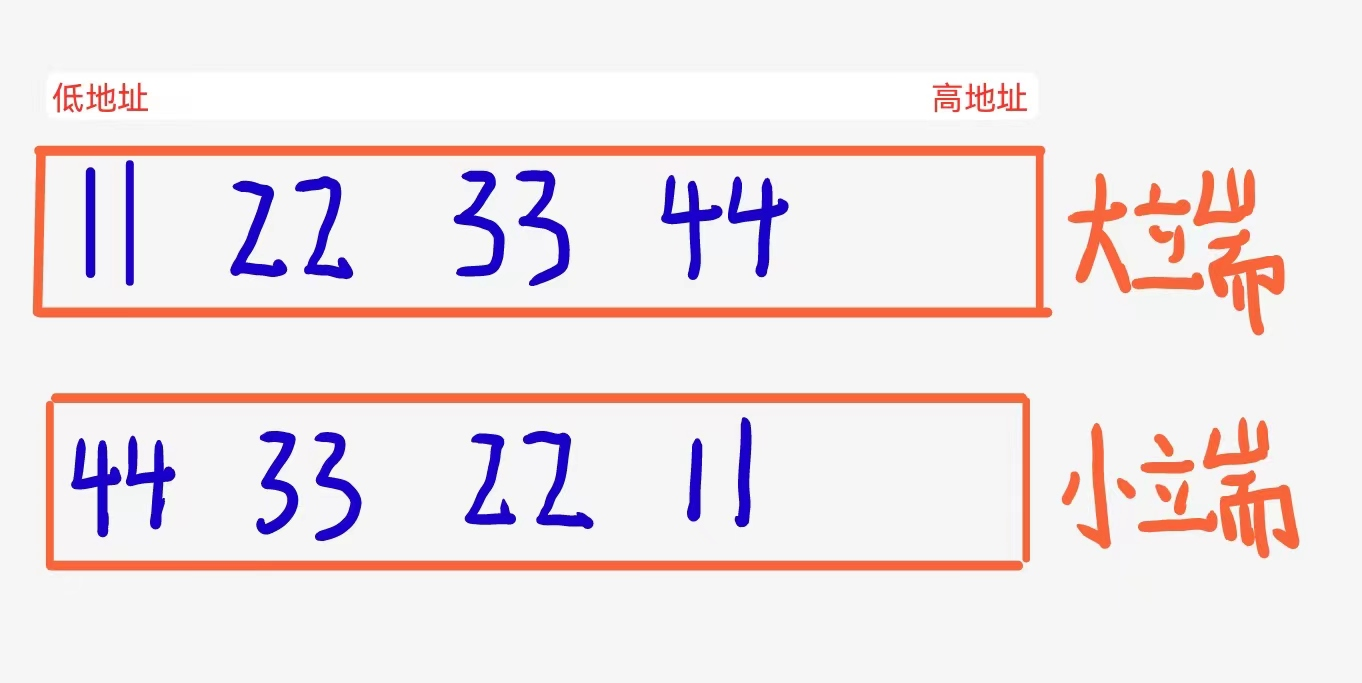
我们说内存分为高地址和低地址,而数据又分高位和低位,比如说这里 11223344 的44 就是数据的低位,而 11 就是数据的高位,下面我给出大小端的定义:

• 大端字节序（存储）模式，是指数据的低位保存在内存的高地址中，而数据的高位，保存在内存的低地址中；
• 小端字节序（存储）模式，是指数据的低位保存在内存的低地址中，而数据的高位,，保存在内存的高地址中。

字节序—就是以字节为单位,讨论存储顺序的.这里的 11 为一个字节, 22 为一个字节,整型共四个字节

---

---

3.1 为什么有大端小端?🏁

为什么会有大小端模式之分呢？这是因为在计算机系统中，我们是以字节为单位的，每个地址单元都对应着一个字节，一个字节为8 bit。但是在C语言中除了8 bit的char之外，还有16 bit的short型，32 bit的long型（要看具体的编译器），另外，对于位数大于8位的处理器，例如16位或者32位的处理器，由于寄存器宽度大于一个字节，那么必然存在着一个如何将多个字节安排的问题。因此就导致了大端存储模式和小端存储模式。

例如：一个 16bit 的 short 型 x ，在内存中的地址为 0x0010 ， x 的值为 0x1122 ，那么 0x11 为高字节， 0x22 为低字节。对于大端模式，就将 0x11 放在低地址中，即 0x0010 中， 0x22 放在高地址中，即 0x0011 中。小端模式，刚好相反。我们常用的 X86 结构是小端模式，而 KEIL C51 则为大端模式。很多的ARM，DSP都为小端模式。有些ARM处理器还可以由硬件来选择是大端模式还是小端模式。

---

3.2 怎样判断大小端🏁

怎么写一个代码判断当前机器是大端还是小端? 这里我们定义一个整型变量a的值为1

它在大小端机器上应该是这样存储的:

---

我们想到,int类型的指针解引用可以访问四个字节的空间,而char类型的指针解引用可以访问一个字节的空间,我们定义一个char类型的指针指向变量a,如果对指针解引用的结果是1,那么当前机器就是小端,解引用后结果是0那么机器就是大端.

#include<stdio.h>int main()
{int a = 1;char* p = (char*)&a;//强制类型转换,否则会报警告if (*p == 1){printf("当前机器为小端");}else{printf("当前机器为大端");}return 0;
}

---

4. 类型的范围🚩

我们把整型家族划分为:

下面我们主要来讨论 char 类型的范围,并做一些练习

---

4.1 char 类型的范围🏁

我们知道char类型在内存中占1个字节,也就是八个比特位(也可以说占八个二进制位),我们来讨论一下有符号char和无符号char的数据存储范围.

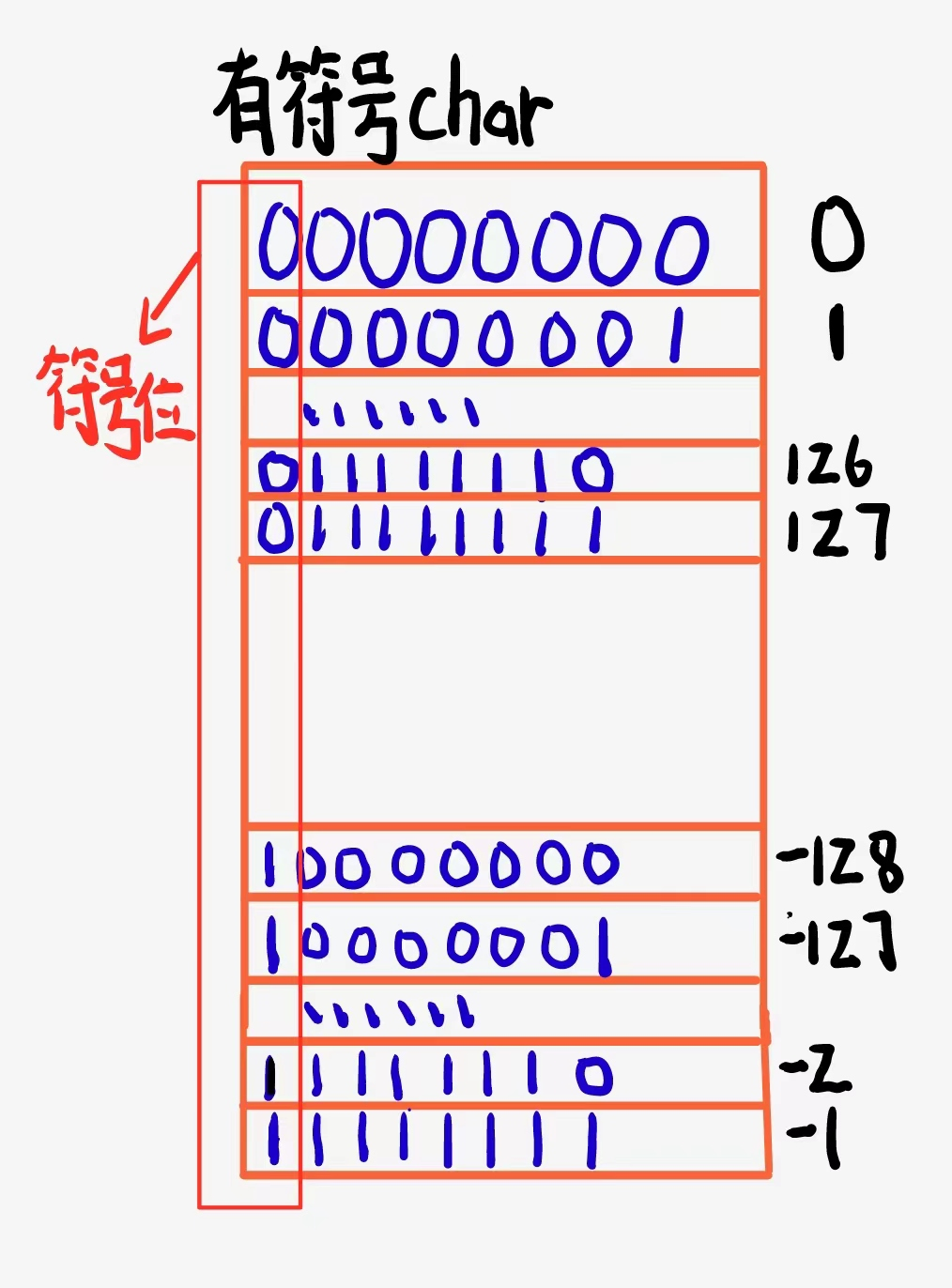
再来看看无符号位的存储:

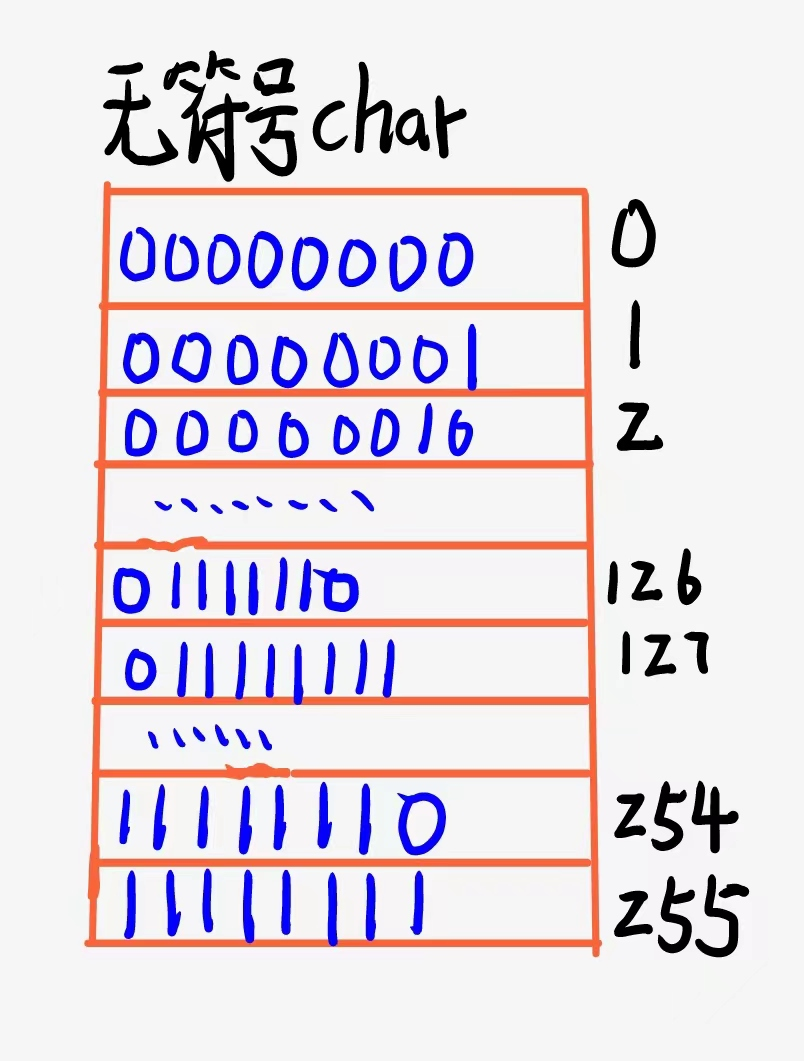
• 有符号位char的范围: -128~127
• 无符号位char的范围: 0~255

并且我们可以发现一个规律,无符号char中,255+1,又跳到0去了,形成了一个循环,所以我们可以画这样一个圆形的循环图来理解:

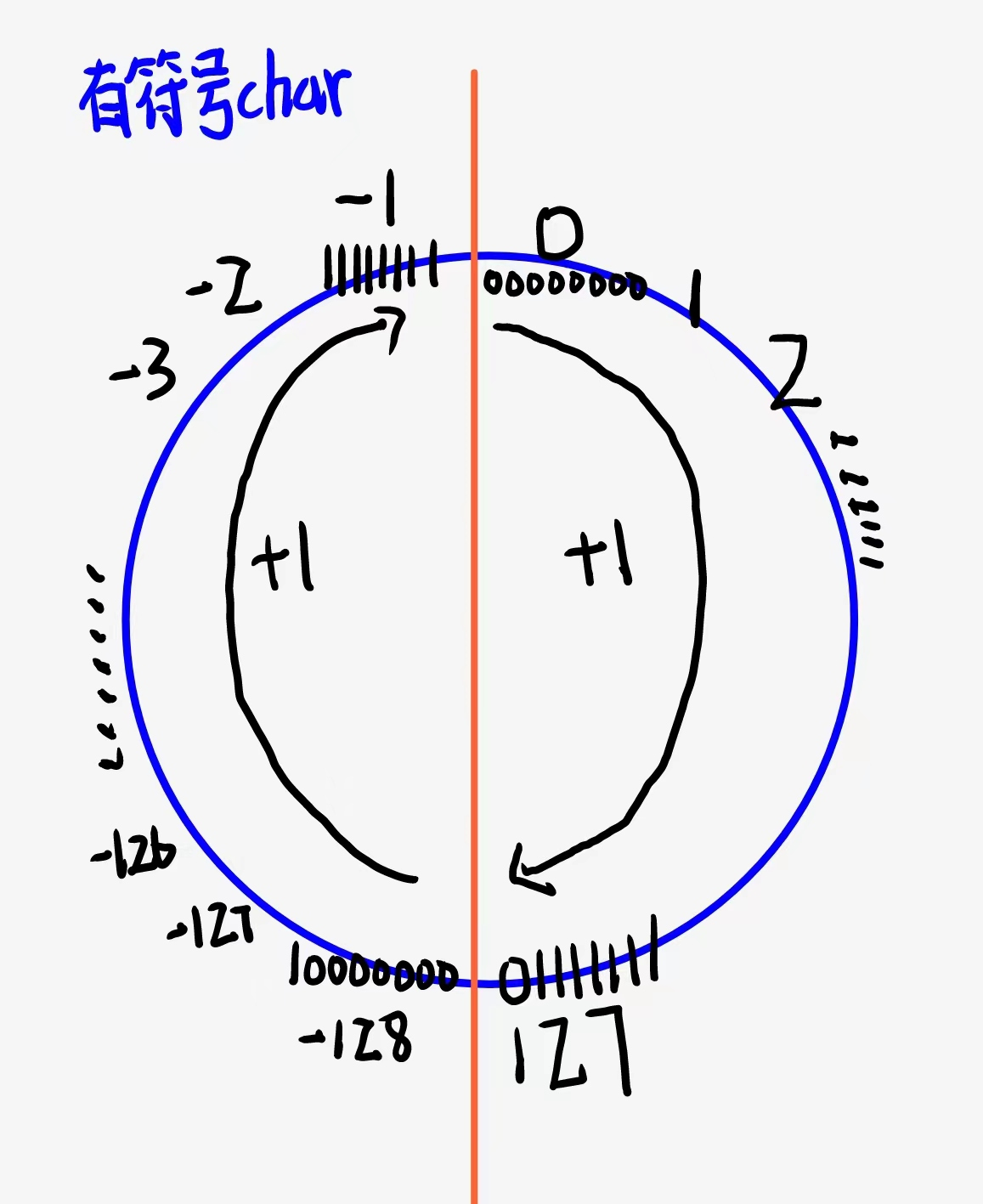
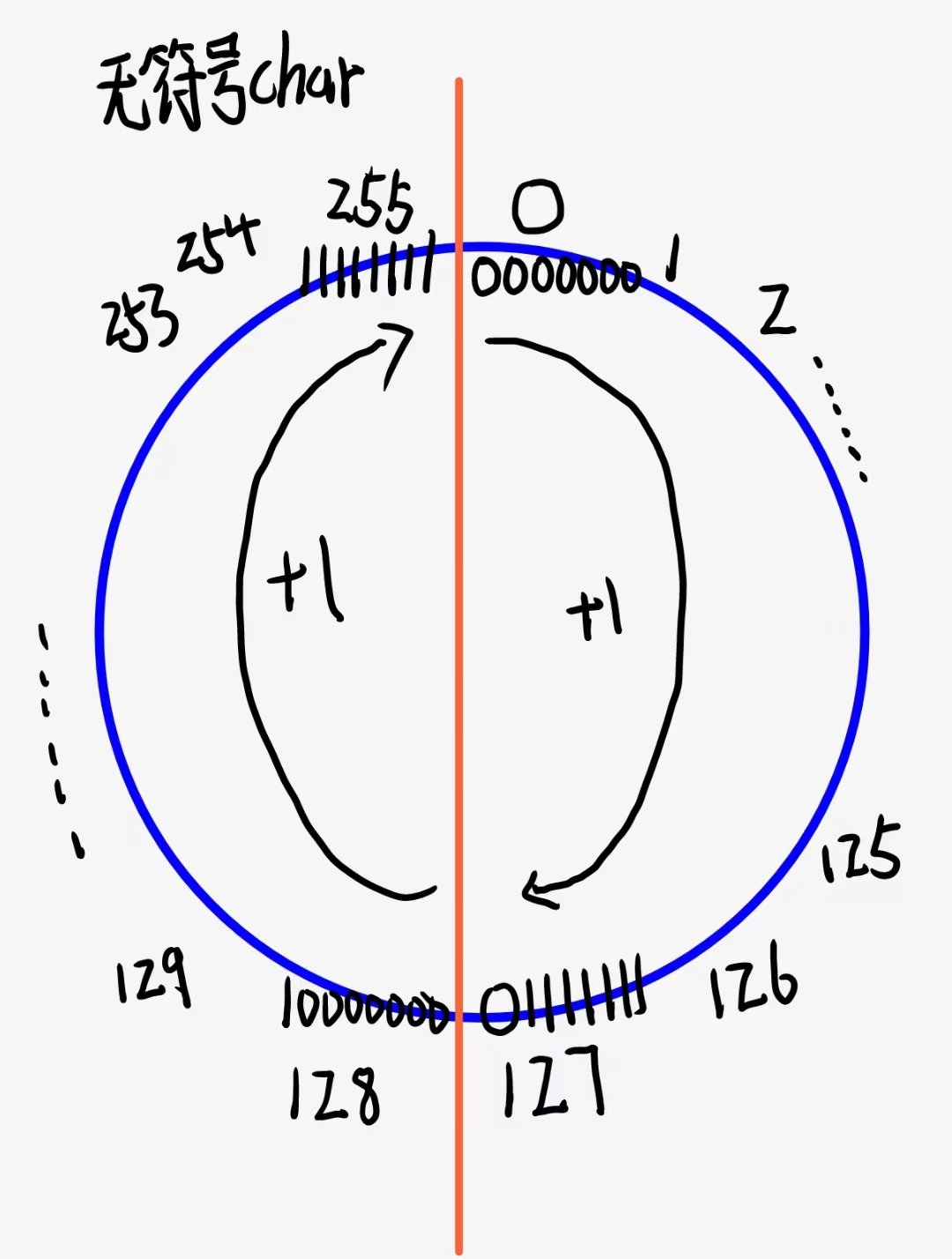
我们可以看见,无符号位的char的127+1变成了128,而有符号位的char中的127+1变成了-128.并且无符号位中的255加1又回到了0,所以无符号char能存储的最大数就是255.超过255又会重新回到0.

---

5. 练习🚩

5.1 练习一🏁

1.
//输出什么？
#include <stdio.h>
int main()
{char a= -1;signed char b=-1;unsigned char c=-1;printf("a=%d,b=%d,c=%d",a,b,c);return 0;
}

这里a和b很好判断,在vs编译器下,如果没有指定是否是有符号或者无符号,就默认为有符号形,然而c是无符号char类型的变量,它存储-1的补码在内存中,-1的补码是 11111111 然而无符号数的源反补码都相同,所以当-1被存储在无符号数中后,11111111八个1都不是符号位,值就为255了.

---

5.2 练习二🏁

2.
#include <stdio.h>
int main()
{char a = -128;printf("%u\n",a);return 0;
}

首先这里会输出4294967168,为什么呢?首先a是有符号char类型的变量,存储-128的值,然而%u是打印无符号整数的意思,所以这里的char类型会发生整型提升,从一个字节提升至4个字节,又因为a是负数,它的的符号位为1,所以整型提升时前面全部都是补的1,所以我们就得到了一个数的补码,然而无符号数的源反补码都相同,所以我们就会得到一个特别大的数的源码.

---

5.3 练习三🏁

3.
unsigned int i;
for(i = 9; i >= 0; i--)
{printf("%u\n",i);
}

这里会死循环打印,我们来分析分析,这里的变量 i 是无符号整型,一个无符号数是肯定不会是负数的,当 i 等于0时再减去1,它会像我们刚刚讨论的无符号char类型一样变成无符号整型中的最大值,而不是-1,所以它会一直打印下去

这里给大家看一看现象:

---

5.4 练习四🏁

4.
int main()
{char a[1000];int i;for(i=0; i<1000; i++){a[i] = -1-i;}printf("%d",strlen(a));return 0;
}

这里数组a的长度为255,我们来分析这一点.首先,数组a中存储的数据是有符号char类型的数据,数据范围是: -128 ~ 127之间.这里循环中 i 的范围是: -1 ~ -999 之间,数组中的内容会从-1开始一直往后存储,当i等于-128时,-1-128这时根据我们上面画的循环图,-1-128就等于127.下一步-1-129同理也就是等于126,然后125,124…这样存储下去,直到它变为0后又减一变成-1,以此循环往复直到装满1000个数为止.

当我们分析到这里还没有结束,我们知道这1000个元素其实就是 -128~127之间所有的数重复了几遍组成的,然而我们知道 strlen操作符的结束标志是遇见’\0’, 并且’\0’的ASCLL值是0,也就是说当strlen遇见0时,它就会终止,在外面数组中遇见的第一个0就会被系统当作数组的长度,根据外面刚才的分析,可以得出,第一个0出现时有128+127=255个元素已经在数组中,所以系统会认为数组的长度为255.也就是打印255.

---

5.5 练习五🏁

5.
#include <stdio.h>
unsigned char i = 0;
int main()
{for(i = 0;i<=255;i++){printf("hello world\n");}return 0;
}

这个代码也会死循环打印hello world,这是因为当循环走到 i 等于255时, i 再加一其实不是256,因为无符号char类型能够存储的最大数就是255,根据外面刚刚画的循环图,255加一后就会重新走到0,以此一直循环下去.

---

6. 总结🚩

在数据的存储中,还有一个比较重要的点是浮点型在内存中的存储,这个部分放在下一章节讲解.

🔎 下期预告: C语言进阶 🔍 \

---