机器人学——3.4-轨迹规划

机器人学中最常见的要求之一，是把机器人末端执行器平滑地从位姿 $A$ 移动至位姿 $B$ 。基于之前讨论过的轨迹的内容，我们将讨论两种方法来产生轨迹：在关节空间中的直线和在笛卡儿空间中的直线。这两种直线分别被称为关节空间运动和笛卡儿空间运动。

关节空间运动

我们考虑末端执行器在两个笛卡儿位姿之间移动：

>> T1 = transl(0.4, 0.2, 0) * trotx(pi);
>> T2 = transl(0.4, -0.2, 0) * trotx(pi/2);

它们位于 $x y$ 平面内，且末端执行器指向朝下。与这两个位姿对应的初始和最终关节坐标向量为

>> q1 = p560.ikine6s(T1);
>> q2 = p560.ikine6s(T2);

而我们要求整个运动发生在 $2$ 秒时间内，采样时间间隔为 $50$ 微秒。

>> t = [0:0.05:2]';

通过在q1和q2两个位形之间的平滑插值就能得到一个关节空间轨迹。我们可以用之前的标量插补函数tpoly或lspb，再配合多轴驱动函数mtraj一起实现：

>> q = mtraj(@tpoly, q1, q2, t);

或

>> q = mtraj(@lspb, q1, q2, t);

其结果是得到一个 $50 \times 6$ 阶的矩阵q，其中每行对应一个采样 time step，每列对应一个关节值。但在这里及以后，我们将使用jtraj这个更方便的函数：

>> q = jtraj(q1, q2, t);

其作用相当于具有tpoly插值的mtraj，但它对多轴情况进行了优化，而且还允许使用额外的参数来设置初始和最终速度。对于mtraj+tpoly，最后一个参数可以是一个时间向量，如示例，或者是一个指定采样时间步数的整数。

我们可以通过可选的输出参数，获得随时间变化的关节速度和加速度向量：

>> [q,qd,qdd] = jtraj(q1, q2, t);

SerialLink类中的jtraj方法为上述步骤提供了一个更简洁的表达方式：

>> q = p560.jtraj(T1, T2, t);

所得轨迹可以绘制出动画进行观察：

>> p560.plot(q)

我们也可以绘制出关节角的图形，例如所有随时间变化的关节角：

>> plot(t, q)

在这里插入图片描述
关节坐标轨迹虽然是平滑的，但我们并不知道机器人末端执行器在笛卡儿空间中将如何移动。然而通过将正运动学作用于关节坐标轨迹，可以很容易地确定其效果

>> T = p560.fkine(q);

其结果得到一个三维的笛卡儿轨迹。该轨迹的位移部分为

>> p = transl(T)；
>> about(p)
p [double] : 41x3 (984 bytes)

其中，每一行代表一个采样时间上的末端执行器位置向量。绘制出的各坐标分量随时间变化的图形如图所示。
在这里插入图片描述
我们也可以绘制出末端执行器在 $x y$ 平面内的轨迹：

>> plot(p(:,1), p(:,2))

在这里插入图片描述
显然，这条轨迹不是一条直线。这是预料之中的，因为我们仅仅指定了两个端点的笛卡儿坐标。当机器人在运动过程中旋转其腰部关节时，末端执行器的运动轨迹会自然地划出一个圆弧。在实际工作中，这可能会导致机器人和附近物体之间发生碰撞，即使它们不在位姿A和B之间的路径上。

我们还可以绘制出末端执行器的姿态随时间变化的图形（横滚-俯仰-偏航角形式）：

>> plot(t, tr2rpy(T))

在这里插入图片描述
注意初始横滚角显示为 $-\pi$ ，但在下一个采样时间步它变为 $\pi$ 。这是一个有限精度算法的产物，且这两个角度在圆周上是等价的。

我们也可以在 Simulink 中实现上述示例：

>> mdl_puma560
>> sl_jspace

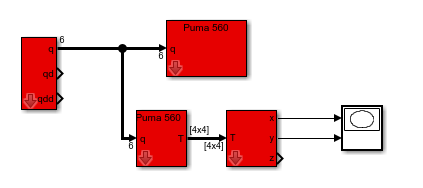
其框图模型如图所示。jtraj模块的参数是关节坐标的初始值和最终值，以及运动的持续时间（Simulink 的积分时间需要设置为等于运动段时间，设置可以通过Simulation菜单或通过 MATLAB 命令>> sim('sl_jspace','10);）。平滑变化的关节角被分成两路传送，一路到plot模块中，该模块能在一个单独的窗口中显示机器人运动的动画；另一路到fkine模块用于计算机器人的正运动学。plot和fkine两个模块有一个共同的SerialLink对象参数，本示例中该参数为p560。使用T2xyz模块能够将末端执行器位置中的笛卡儿位置提取出来，它类似于工具箱函数transl。XY Graph模块可以绘制随x变化的y。
在这里插入图片描述

笛卡尔运动

前面是在位形空间中做直线运动而笛卡尔空间不为直线，现在我们讨论在笛卡尔空间中的直线运动。可以通过使用工具箱函数ctraj来实现，这个函数之前已经介绍过。它的用法与jtraj很相似：

>> Ts = ctraj(T1, T2, length(t));

其输入参数是初始和最后的位姿，以及时间步数，它返回的是一个三维矩阵形式的轨迹。
对于前面的关节空间运动的例子，我们将提取并绘制其位置分量：

>> plot(t, transl(Ts))

在这里插入图片描述
以及姿态分量：

>> plot(t, tr2rpy(Ts))

在这里插入图片描述
各分量的运动以及 $x y$ 平面内末端执行器的路径如下图所示。相比关节空间运动的图，我们注意到一些重要的差异。第一，笛卡尔运动中的位置和姿态随时间线性变化。姿态的俯仰角是为零的常数且不随路径变化。其次，末端执行器在 $x y$ 平面内沿着一条直线运动。
在这里插入图片描述

>> qc = p560.ikine6s(Ts);
>> qplot(t, qc);

在这里插入图片描述

通过奇异点的运动

我们特意选择一个通过机器人奇异点的运动轨迹。我们将先前示例中的笛卡儿端点变为

>> T1 = transl(0.5, 0.3, 0.44) * troty(pi/2);
>> T2 = transl(0.5, -0.3, 0.44) * troty(pi/2);

其结果是得到一个沿着 $y$ 方向的运动，且末端执行器的 $z$ 轴指向 $x$ 方向。其笛卡儿路径是

>> Ts = ctraj(T1, T2, length(t));

我们将其转换到关节坐标：

>> qc = p560.ikine6s(Ts);

在这里插入图片描述

各关节轨迹如图所示。在 $t\approx 0.7s$ 时，我们观察到手腕关节角度 $q_4$ 和 $q_6$ 的变化率非常高。其原因是 $q_5$ 几乎已经为零，这意味着 $q_4$ 和 $q_6$ 的旋转轴几乎对齐重合了，也就是万向节死锁情况或奇异点。

关节轴重合意味着该机器人已经失去了一个自由度，实际上现在是一个五轴机器人。从运动学上我们只能求解出 $q_4+q_6$ 的和值，而针对同一个和值可以有无数的 $q_4$ 和 $q_6$ 解。但如果是采用两个位姿之间的关节空间运动，则可以避免上述问题，因为它不需要求解逆运动学。然而，关节空间运动不会在整个路径中始终维持工具在 $x$ 方向上的姿态，除了在两个端点。广义逆运动学的方法ikine能很容易地处理奇异性问题。