1、AVL树的概念

2、AVL树定义节点

3、AVL树的插入

4、AVL树的旋转

4.1、新节点插入较高左子树的左侧——右单旋

4.2、新节点插入较高右子树的右侧——左单旋

4.3、新节点插入较高左子树的右侧——左右双旋

4.4、新节点插入较高右子树的左侧——右左双旋

5、AVL树的验证

代码汇总：

6、AVL树的删除

7、AVL树性能分析

1、AVL树的概念

AVL树可能是一颗空树，或者是一颗具有性质的二叉搜索树：

左右子树都是AVL树
左右子树高度之差【即平衡因子】的绝对值不超过1

注：

如果一棵二叉搜索树是高度平衡的，他就是AVL树
如果他有n个节点，其高度可保持在O(logn)，搜索时间复杂度：O(logn)
当前节点的平衡因子 = 右子树高度 - 左子树高度

例：

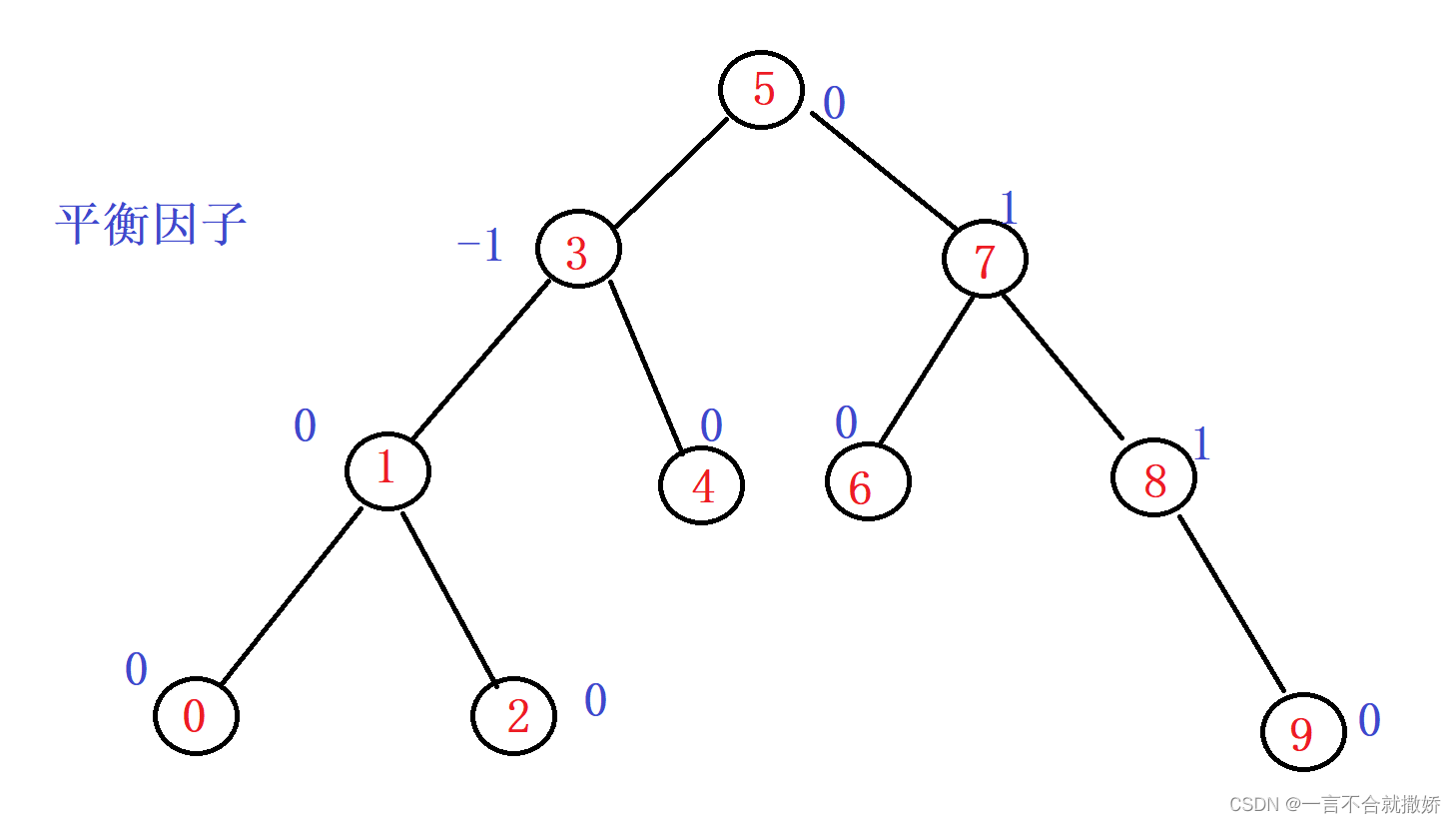
2、AVL树定义节点


public class AVLTree {static class TreeNode {public int val;public int bf;//平衡因子public TreeNode left;//左孩子引用public TreeNode right;//右孩子引用public TreeNode parent;//父节点引用public TreeNode(int val) {this.val = val;}}public TreeNode root;//根节点
}

3、AVL树的插入

AVL树就是在二叉搜索树的基础上引入了平衡因子，因此，AVL树的插入，咱们呢，就可以分为两步：

按照二叉搜索树的方式插入新的节点
调整节点的平衡因子

代码：

     /*** 插入新的节点* @param val* @return 插入成功，返回true，失败返回false*/public boolean insert(int val) {//1、按照二叉搜索树的方式插入新的节点if(root == null) {root = new TreeNode(val);return true;}TreeNode node = new TreeNode(val);TreeNode parent = null;TreeNode cur = root;while(cur != null) {if(cur.val < val){parent = cur;cur = cur.right;} else if(cur.val == val) {return false;} else {parent = cur;cur = cur.left;}}if(parent.val < val) {parent.right = node;} else {parent.left = node;}node.parent = parent;cur = node;//2、调节平衡因子}

看一个例子：

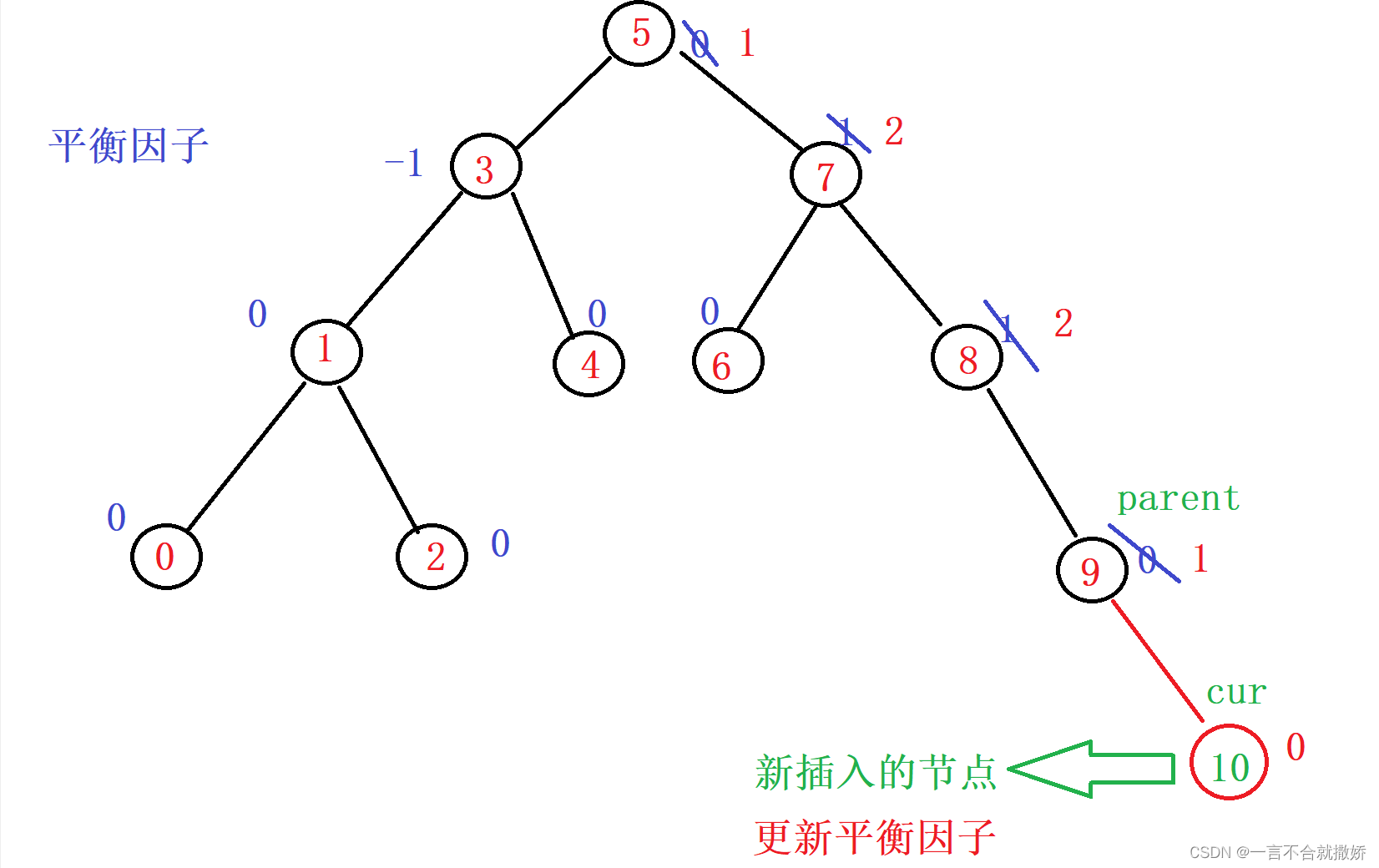
调节平衡因子，需要注意的点：

cur插入后，parent的平衡因子一定需要调整，在插入之前，parent的平衡因子分为三种情况：-1，0, 1, 分以下两种情况：

如果cur插入到parent的左侧，只需给parent的平衡因子-1即可
如果cur插入到parent的右侧，只需给parent的平衡因子+1即可

平衡因子更新时，存在一个问题，我们需要更新到什么时候停止呢？难道每次都要更新到根节点？

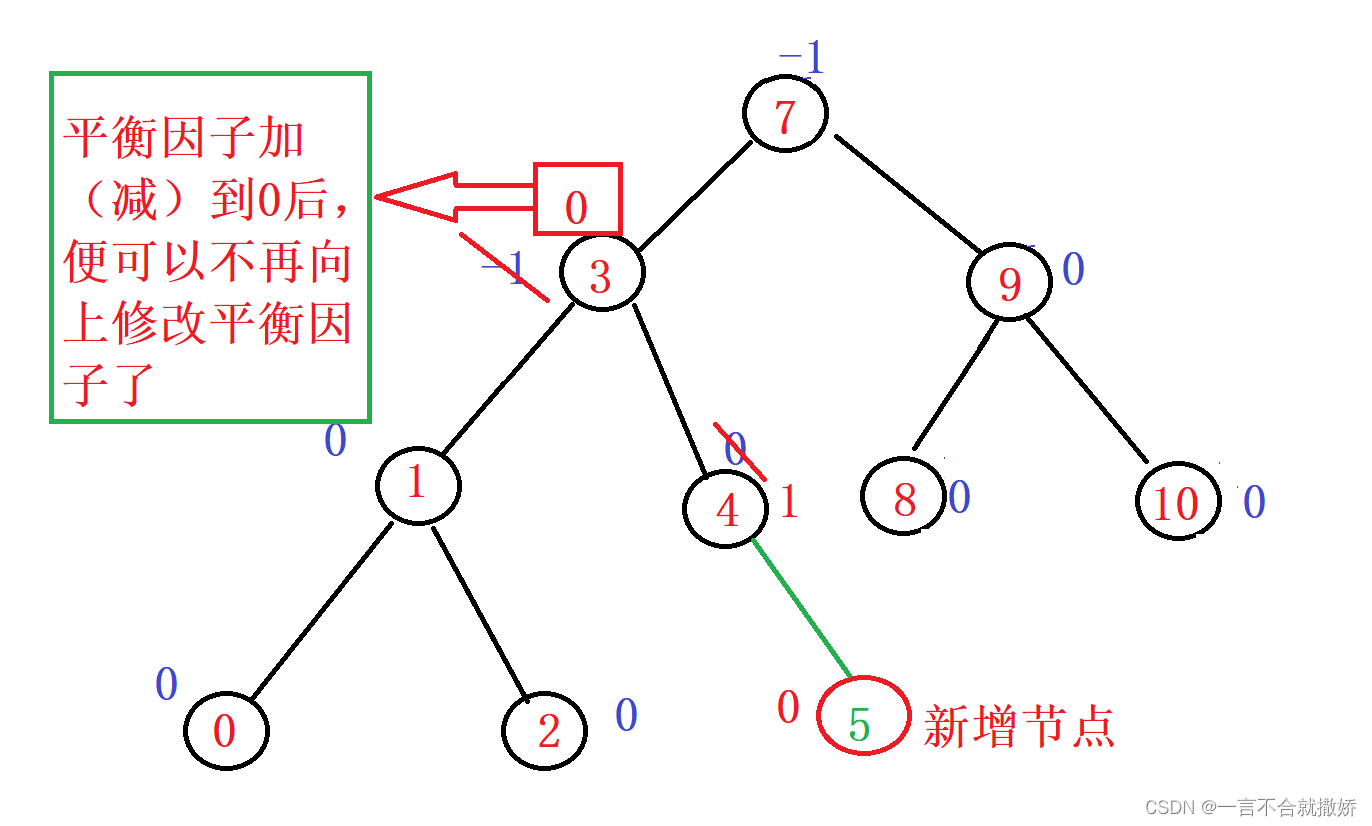
此时：parent的平衡因子可能有三种情况：0，正负1，正负2

如果parent的平衡因子为0，说明插入之前parent的平衡因子为正负1，插入后被调整成0，此时满足AVL树的性质，插入成功
如果parent的平衡因子为正负1，说明插入前parent的平衡因子一定为0，插入后被更新成正负1，此时以parent为根的树的高度增加，需要继续向上更新
如果parent的平衡因子为正负2，则parent的平衡因子违反平衡树的性质，需要对其进行旋转处理

先看目前我们所能写出来的代码：

        //2、修改平衡因子//循环条件，暂时不看while () {//先看cur是parent的左还是右，决定平衡因子是加1还是减1if(cur == parent.right) {//右树高度增加，平衡因子++parent.bf++;} else {//左树高度增加，平衡因子--parent.bf--;}if(parent.bf == 0) {break;//已经平衡了} else if(parent.bf == 1 || parent.bf == -1) {//需要继续向上检查cur = parent;parent = parent.parent;} else {//需要左/右旋转if(parent.bf == 2) {//右树高----需要降低右树的高度if(parent.bf == 1) {} else {//parent.bf == -1}} else{//parent.bf == -2//左树高----需要降低左树的高度if(parent.bf == -1) {} else {//parent.bf == 1}}}}

接下来，需要做的是，填充各个情况下，是需要将树进行左旋还是右旋

4、AVL树的旋转

4.1、新节点插入较高左子树的左侧——右单旋

流程：

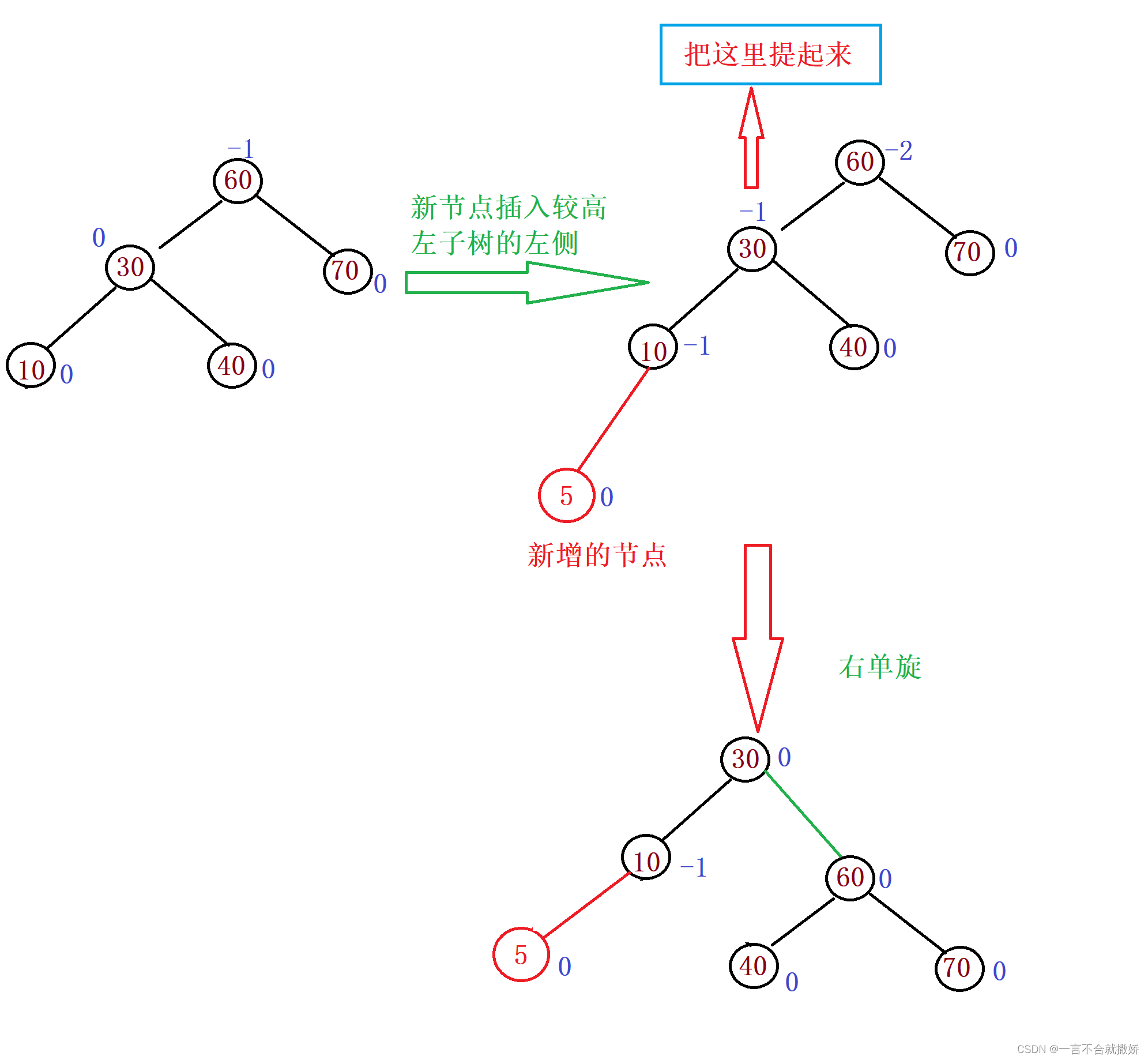
具体实现：

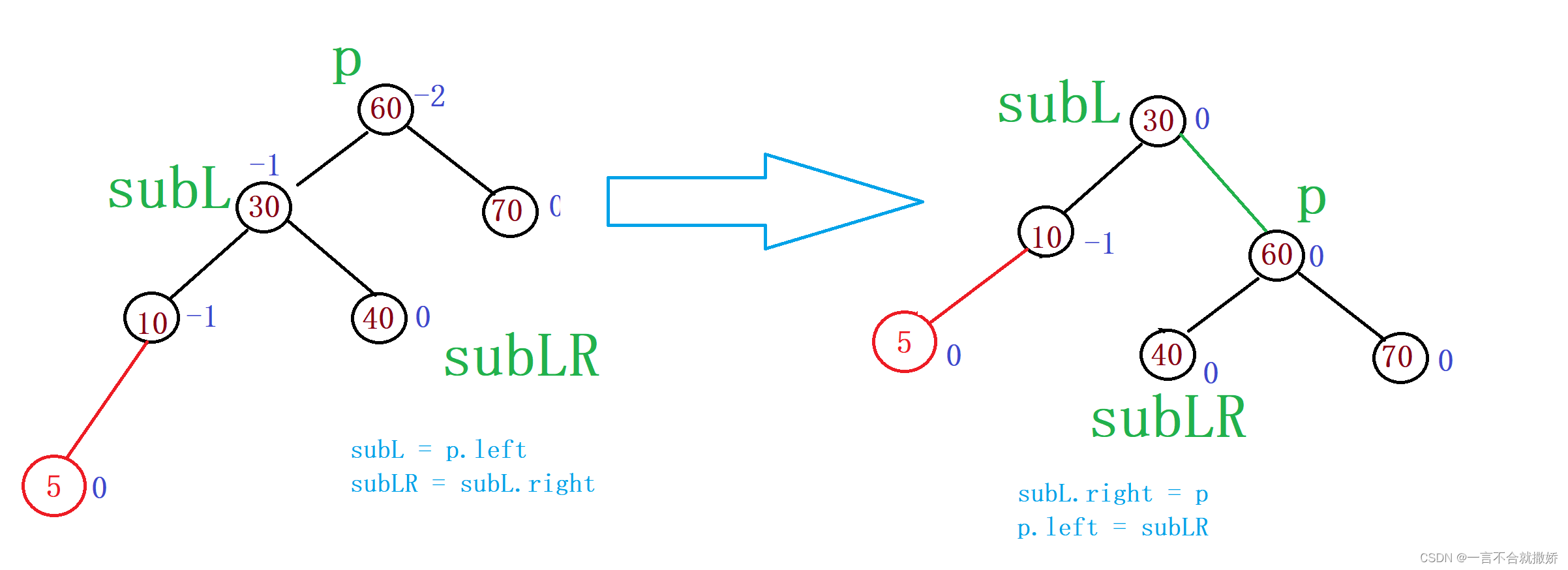
另外p还需要考虑的情况：

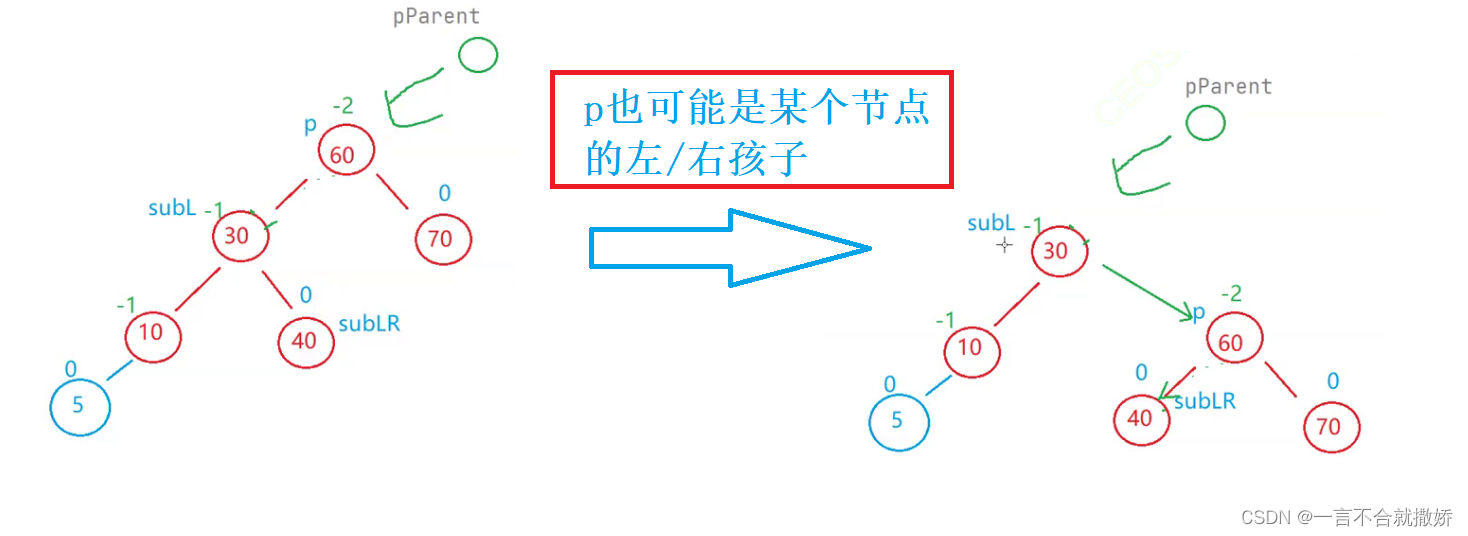
代码：

    /*** 右单旋* @param parent*/private void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;parent.left = subLR;subL.right = parent;//没有subLRif(subLR != null) {subLR.parent = parent;}//记录p的父节点TreeNode pParent = parent.parent;parent.parent = subL;//检查当前是不是根节点if(parent == root) {root = subL;root.parent = null;} else {//不是根节点//判断左右树if(pParent.left == parent) {pParent.left = subL;} else {pParent.right = subL;}subL.parent = pParent;}subL.bf = 0;parent.bf = 0;}

4.2、新节点插入较高右子树的右侧——左单旋

流程：

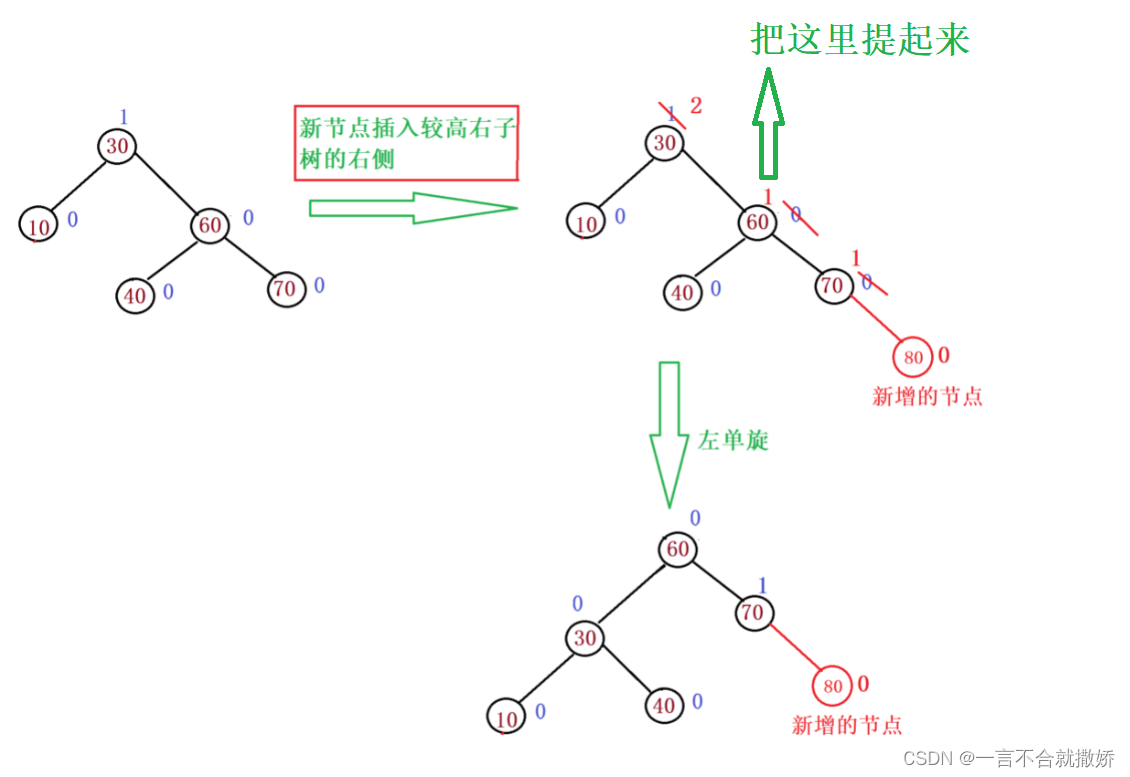
具体实现：

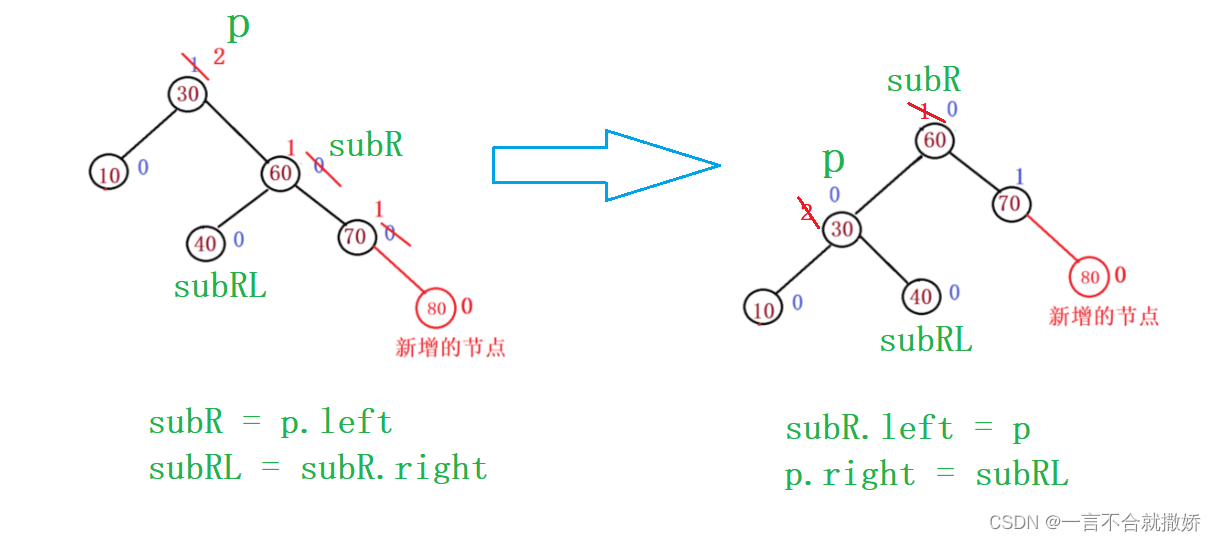
同上述的右旋，p单独考虑的情况【p也可能会是某个节点的左/右孩子】

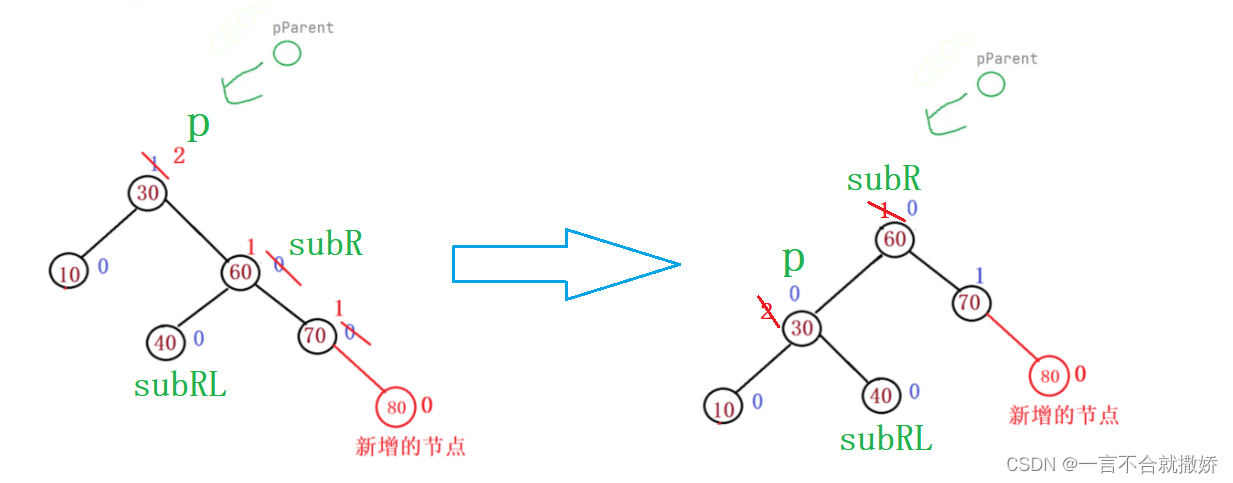
代码：

     /*** 左单旋* @param parent*/private void rotateLeft(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;parent.right = subRL;if(subRL != null) {subRL.parent = parent;}TreeNode pParent = parent.parent;parent.parent = subR;if(root == parent) {root = subR;root.parent = null;} else {if (pParent.left == parent) {parent.left = subR;} else {parent.right = subR;}subR.parent = pParent;}subR.bf = 0;parent.bf = 0;}

4.3、新节点插入较高左子树的右侧——左右双旋

流程：

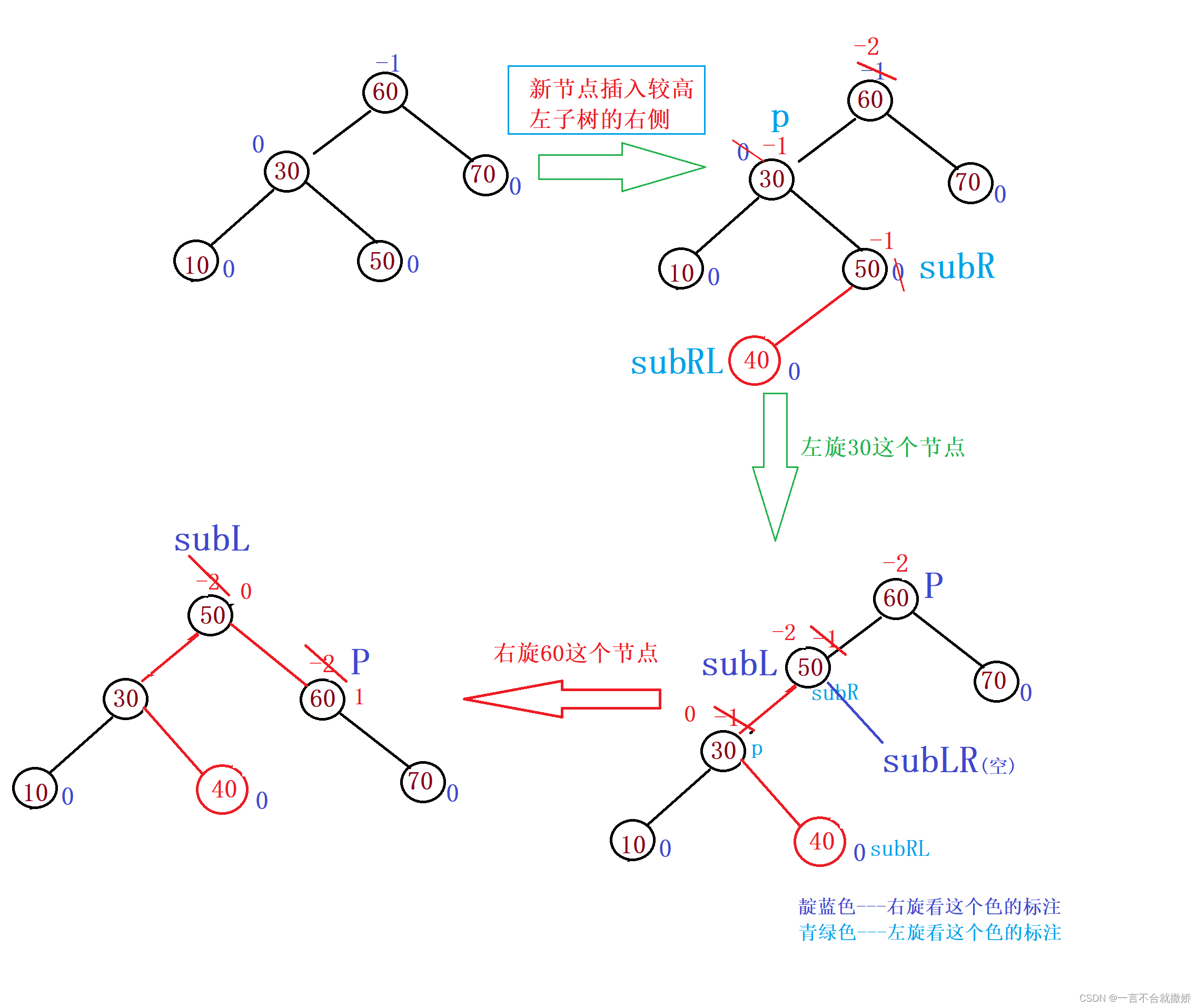
当插入的值是55的时候，就是插入在50的右边，也是左右双旋，但是最终的平衡因子的更改略有差异，可以自己试着画一画。

代码：

    /*** 左右双旋* @param parent*/private void rotateLR(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;int bf = subLR.bf;//左rotateLeft(parent.left);//右rotateRight(parent);if(bf == -1) {subL.bf = 0;subLR.bf = 0;parent.bf = 1;} else if(bf == 1) {subL.bf = -1;subLR.bf = 0;parent.bf = 0;}}

4.4、新节点插入较高右子树的左侧——右左双旋

流程：

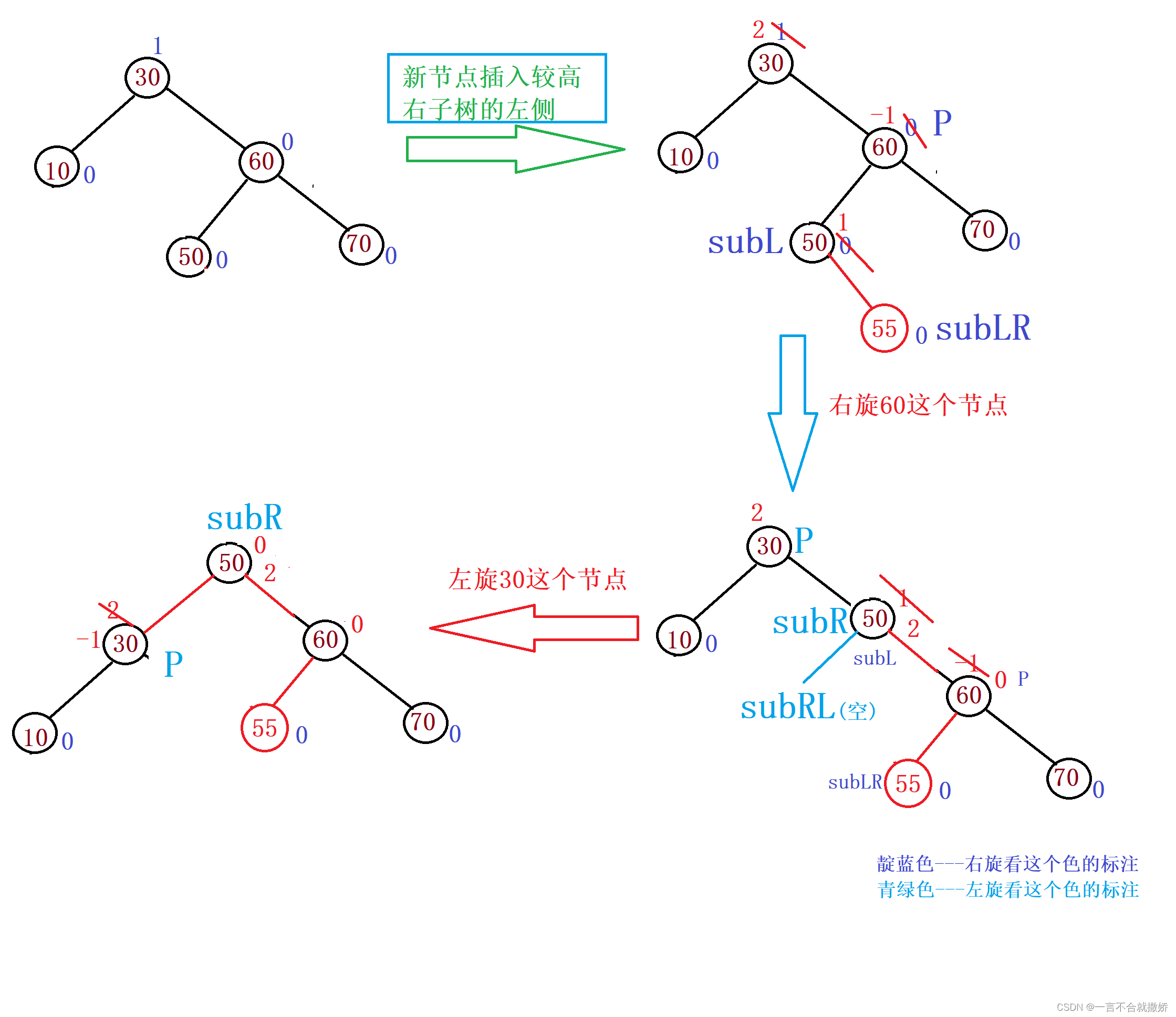
当插入的值是40的时候，就是插入在50的左边，也是右左双旋，但是最终的平衡因子的更改略有差异，可以自己试着画一画。

代码：

    /*** 右左双旋* @param parent*/private void rotateRL(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;int bf = subRL.bf;rotateRight(parent.right);rotateLeft(parent);if(bf == 1) {parent.bf = -1;subR.bf = 0;subRL.bf = 0;} else {parent.bf = 0;subR.bf = 1;subRL.bf = 0;}}

5、AVL树的验证

同插入类似，由于它是特殊的二叉搜索树，所以验证时，分两步：

验证是否为二叉搜索树
验证是否为平衡树

代码：

    //中序遍历的结果是有序的 就能说明当前树 一定是搜索树public void inorder(TreeNode root) {if(root == null) return;inorder(root.left);System.out.print(root.val+"  ");inorder(root.right);}//计算高度private int height(TreeNode root) {if(root == null) return 0;int leftH = height(root.left);int rightH = height(root.right);return leftH > rightH ? leftH+1 : rightH+1;}//是否高度平衡：public boolean isBalanced(TreeNode root) {if(root == null) return true;int leftH = height(root.left);int rightH = height(root.right);if(rightH-leftH != root.bf) {System.out.println("这个节点："+root.val+" 平衡因子异常");return false;}return Math.abs(leftH-rightH) <= 1&& isBalanced(root.left)&& isBalanced(root.right);}

代码汇总：

/*** Created with IntelliJ IDEA.* Description:* User:龙宝* Date:2023-01-10* Time:17:38*/
public class AVLTree {static class TreeNode {public int val;public int bf;//平衡因子public TreeNode left;//左孩子引用public TreeNode right;//右孩子引用public TreeNode parent;//父节点引用public TreeNode(int val) {this.val = val;}}public TreeNode root;//根节点/*** 插入新的节点* @param val* @return 插入成功，返回true，失败返回false*/public boolean insert(int val) {//1、按照二叉搜索树的方式插入新的节点if(root == null) {root = new TreeNode(val);return true;}TreeNode node = new TreeNode(val);TreeNode parent = null;TreeNode cur = root;while(cur != null) {if(cur.val < val){parent = cur;cur = cur.right;} else if(cur.val == val) {return false;} else {parent = cur;cur = cur.left;}}if(parent.val < val) {parent.right = node;} else {parent.left = node;}node.parent = parent;cur = node;//2、修改平衡因子while (parent != null) {//先看cur是parent的左还是右，决定平衡因子是加1还是减1if(cur == parent.right) {//右树高度增加，平衡因子++parent.bf++;} else {//左树高度增加，平衡因子--parent.bf--;}if(parent.bf == 0) {break;//已经平衡了} else if(parent.bf == 1 || parent.bf == -1) {//需要继续向上检查cur = parent;parent = parent.parent;} else {if(parent.bf == 2) {//右树高----需要降低右树的高度if(cur.bf == 1) {//左旋rotateLeft(parent);} else {//cur.bf == -1rotateRL(parent);}} else{//parent.bf == -2//左树高----需要降低左树的高度if(cur.bf == -1) {//右旋rotateRight(parent);} else {//cur.bf == 1rotateLR(parent);}}break;}}return  false;}/*** 右单旋* @param parent*/private void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;parent.left = subLR;subL.right = parent;//没有subLRif(subLR != null) {subLR.parent = parent;}//记录p的父节点TreeNode pParent = parent.parent;parent.parent = subL;//检查当前是不是根节点if(parent == root) {root = subL;root.parent = null;} else {//不是根节点//判断左右树if(pParent.left == parent) {pParent.left = subL;} else {pParent.right = subL;}subL.parent = pParent;}subL.bf = 0;parent.bf = 0;}/*** 左单旋* @param parent*/private void rotateLeft(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;parent.right = subRL;if(subRL != null) {subRL.parent = parent;}TreeNode pParent = parent.parent;parent.parent = subR;if(root == parent) {root = subR;root.parent = null;} else {if (pParent.left == parent) {parent.left = subR;} else {parent.right = subR;}subR.parent = pParent;}subR.bf = 0;parent.bf = 0;}/*** 左右双旋* @param parent*/private void rotateLR(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;int bf = subLR.bf;//左rotateLeft(parent.left);//右rotateRight(parent);if(bf == -1) {subL.bf = 0;subLR.bf = 0;parent.bf = 1;} else if(bf == 1) {subL.bf = -1;subLR.bf = 0;parent.bf = 0;}}/*** 右左双旋* @param parent*/private void rotateRL(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;int bf = subRL.bf;rotateRight(parent.right);rotateLeft(parent);if(bf == 1) {parent.bf = -1;subR.bf = 0;subRL.bf = 0;} else {parent.bf = 0;subR.bf = 1;subRL.bf = 0;}}//验证：//中序遍历的结果是有序的 就能说明当前树 一定是AVL树吗？  不一定的public void inorder(TreeNode root) {if(root == null) return;inorder(root.left);System.out.print(root.val+"  ");inorder(root.right);}private int height(TreeNode root) {if(root == null) return 0;int leftH = height(root.left);int rightH = height(root.right);return leftH > rightH ? leftH+1 : rightH+1;}public boolean isBalanced(TreeNode root) {if(root == null) return true;int leftH = height(root.left);int rightH = height(root.right);if(rightH-leftH != root.bf) {System.out.println("这个节点："+root.val+" 平衡因子异常");return false;}return Math.abs(leftH-rightH) <= 1&& isBalanced(root.left)&& isBalanced(root.right);}}