学了一坤时Linux，赶紧来俩道题目放松放松。

T1：在字符串中找出连续最长的数字串

 链接：在字符串中找出连续最长的数字串__牛客网

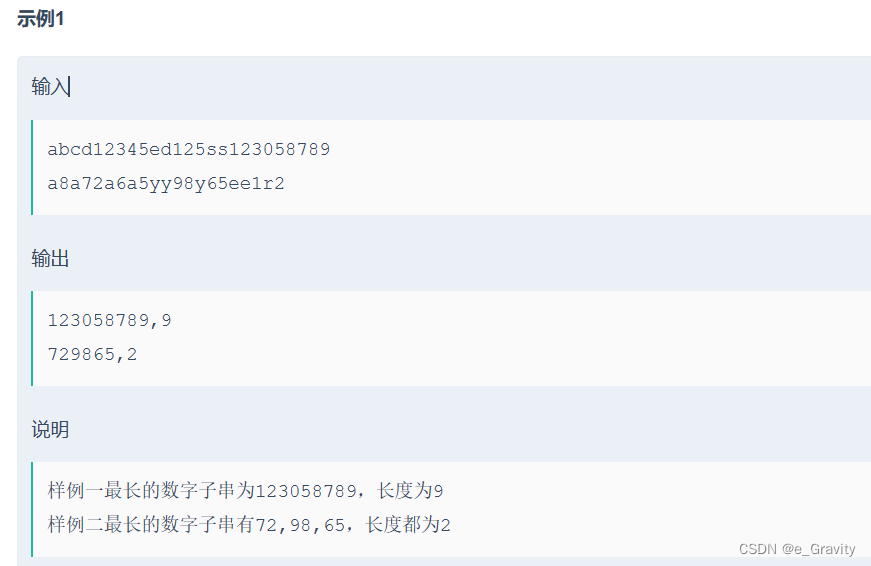
输入一个字符串，返回其最长的数字子串，以及其长度。若有多个最长的数字子串，则将它们全部输出（按原字符串的相对位置）

本题含有多组样例输入。

数据范围：字符串长度 1≤n≤200， 保证每组输入都至少含有一个数字

这题复刻了一道经典dp【力扣53.最大子数组和】,下面是dp的代码

#include<iostream>
#include<string>
#include<vector>
using namespace std;
string s;
int main()
{while(cin>>s){int ans=0;int n=s.size();int cnt=0;string temp;string res;vector<int>dp(n);if(s[0]>='0'&&s[0]<='9') {dp[0]=1;temp+=s[0];}for(int i=1;i<n;i++){if(s[i]>='0'&&s[i]<='9'){dp[i]=dp[i-1]+1;temp+=s[i];}else{dp[i]=0;temp="";}if(dp[i]>ans){res=temp;}else if(dp[i]==ans){res+=temp;}ans=max(ans,dp[i]);}cout<<res<<","<<ans<<endl;}return 0;
}

其实dp数组可以用一个变量代替，代码会更简洁。

#include<iostream>
#include<string>
using namespace std;
string s;
int main()
{while(cin>>s){int ans=0;int n=s.size();int cnt=0;string temp;string res;for(int i=0;i<n;i++){if(s[i]>='0'&&s[i]<='9'){cnt++;temp+=s[i];}else{cnt=0;temp="";}if(cnt>ans){res=temp;}else if(cnt==ans){res+=temp;}ans=max(ans,cnt);}cout<<res<<","<<ans<<endl;}return 0;
}

 

T2：数组中出现次数超过一半的数字

链接：数组中出现次数超过一半的数字__牛客网

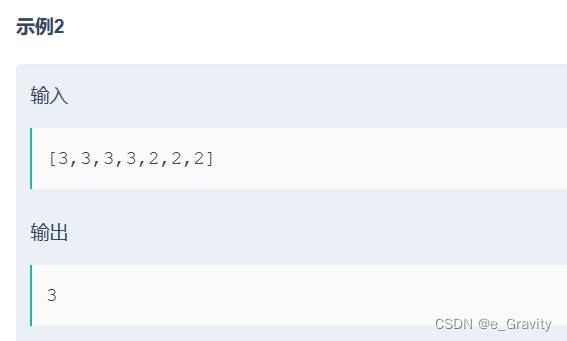
给一个长度为 n 的数组，数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。

例如输入一个长度为9的数组[1,2,3,2,2,2,5,4,2]。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。

数据范围：n≤50000，数组中元素的值 0≤val≤100000

要求：空间复杂度：O(1)，时间复杂度 O(n)

emmm,开始看道这题，容易想到map一遍，但这题的空间复杂度要求是O(1)。

想了用位运算，不过那些是跟奇偶性有关。

如何数组中存在众数，那众数的数量一定大于数组长度的一半。

我们可以用一种消去的思想：比较相邻的俩个数，如果不相等就消去。最坏的情况下，每次都消去一个众数和一个非众数，如果众数存在，那最后留下的一定就是众数。

class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** * @param numbers int整型vector * @return int整型*/int MoreThanHalfNum_Solution(vector<int>& numbers) {// write code hereint cnt=0;int ans=0;int n=numbers.size();for(auto x:numbers){if(!cnt){cnt=1;ans=x;}else{if(ans==x)cnt++;else cnt--;}}cnt=0;for(auto x:numbers){if(x==ans)cnt++;}if(cnt>n/2)return ans;return 0;}
};