二叉树链式结构基础

一、前中后序遍历

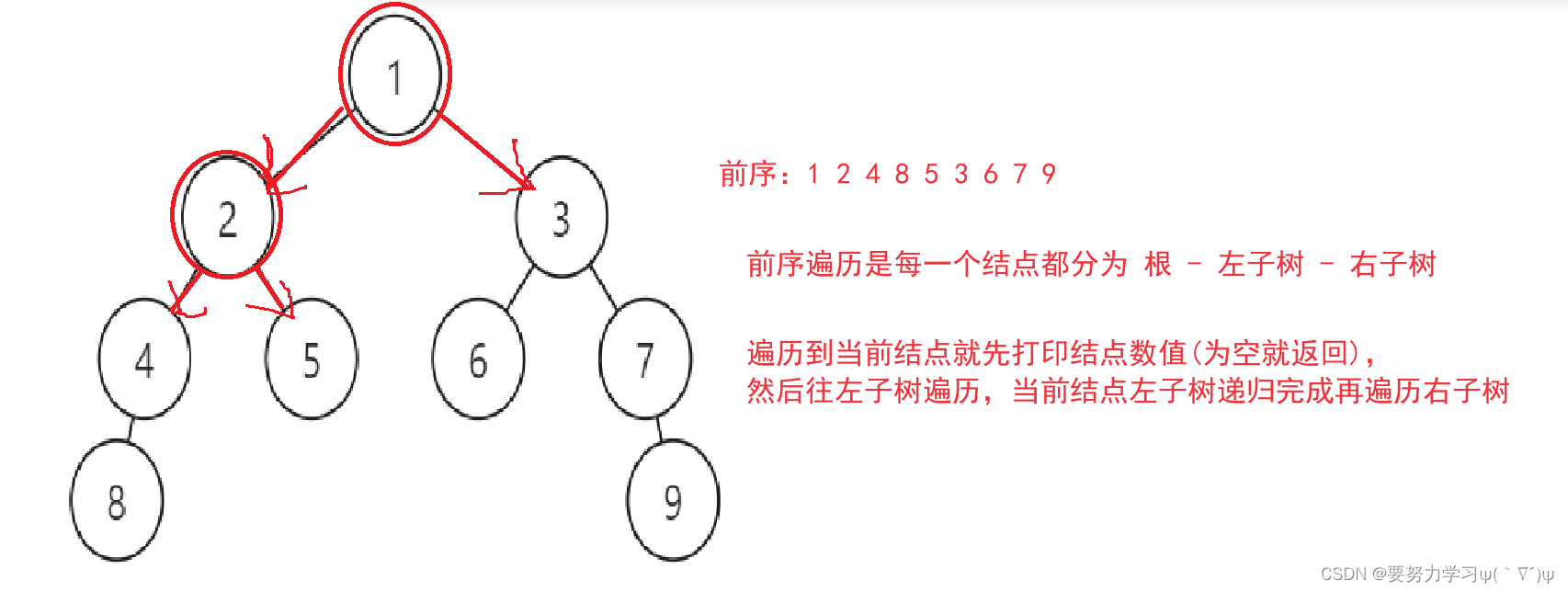
1、前序遍历：前序遍历是采用根 - 左子树 - 右子树的顺序遍历二叉树。

也就是把整棵树分为一个个子问题，每个结点都可以看作根、左子树、右子树三个部分

(左右子树可以为空，就是单节点，根为空就表示探索完成，返回)。

前序遍历就是先保存根，然后向左探索，遇到空回来后向右探索。

当所有结点的根、左子树、右子树都探索完成，整棵树也就探索完成了。

代码如下：

//前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == nullptr)return;printf("%c ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}

可以根据图来看

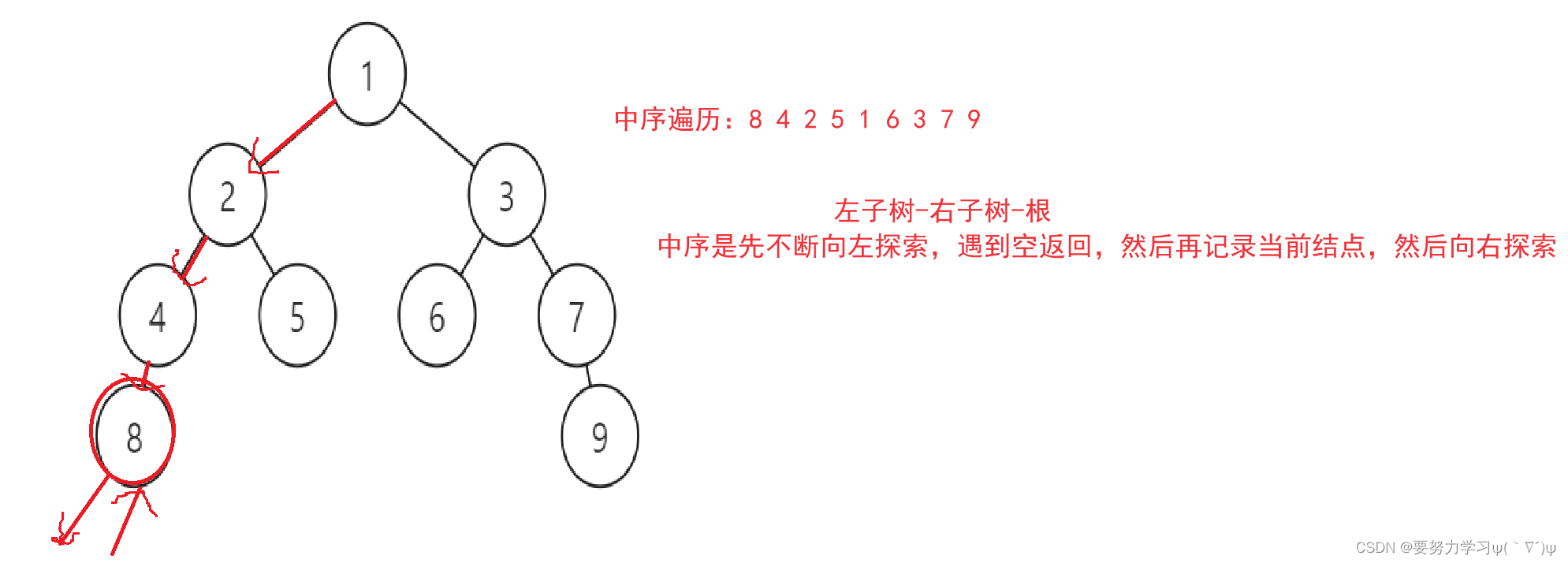
2、中序遍历：中序遍历是采用左子树 - 根 - 右子树的顺序遍历二叉树。

与前序遍历类似，每个结点都可以看作根、左子树、右子树三个部分

不同的是中序遍历是先向左探索，等到为空返回时，再记录当前结点，最后向右探索

代码如下：

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == nullptr)return;BinaryTreePrevOrder(root->_left);printf("%c ", root->_data);BinaryTreePrevOrder(root->_right);
}

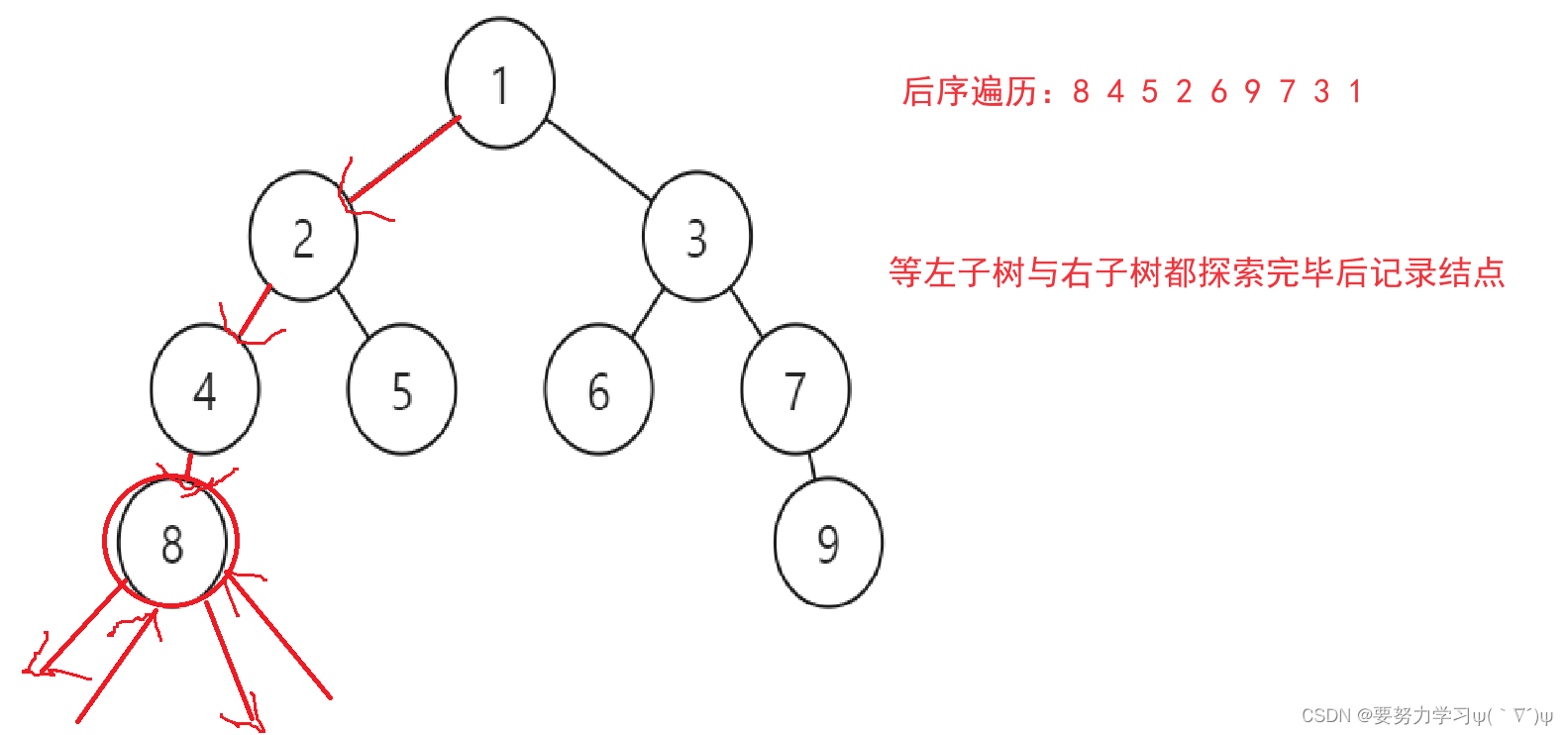
3、后序遍历：后序遍历是采用左子树 - 右子树 - 根的顺序遍历二叉树。

与前序和中序类似，后序是先向左探索，递归返回后向右探索，最后记录根

代码如下：

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == nullptr)return;BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);printf("%c ", root->_data);
}

二、层序遍历

层序遍历：和名字一样，就是一层一层遍历，如上图示例，层序遍历就是

1 2 3 4 5 6 7 8 9

操作方法：先用一个队列保存根结点，然后在出根节点的时候把它的左右不为空的孩子入队列，然后重复先出再入操作。每个父亲结点会在走之前会把自己的孩子都拉进队列(也就是当一层结点遍历完成后，其二层结点已经全部在队列里面了)，所以在遍历过程中栈不会为空，栈为空就代表所有结点都遍历完成，结束循环。

代码如下：

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{queue<BTNode*> q;//队列q.push(root);//先入根节点while (!q.empty())//为空结束{BTNode* tmp = q.front();//取队头数据printf("%c ", tmp->_data);q.pop();//出if(tmp->_left)//把它的非空孩子拉进队列q.push(tmp->_left);if(tmp->_right)q.push(tmp->_right);}
}

三、计算结点个数

分治思想，把整棵树分为根 - 左子树 - 右子树，结点个数就等于左子树 + 右子树 + 1.

代码如下：

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (root == nullptr)return 0;int leftHeight = BinaryTreeSize(root->_left);int rightHeight = BinaryTreeSize(root->_right);return leftHeight + rightHeight + 1;
}

四、查找值为x的结点

查找值为x的结点，遍历查找，前中后序都可以，找到返回即可。

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == nullptr)return nullptr;if (root->_data == x)return root;BTNode* ret1 = BinaryTreeFind(root->_left, x);if (ret1)//如果找到了直接返回，没找到去右边找return ret1;return BinaryTreeFind(root->_right, x);
}

五、销毁二叉树

销毁二叉树：就是将二叉树的所有结点都free掉，也要遍历二叉树。

那该用前序中序还是后序呢？

前序是先将自己干掉，把自己干掉后就找不到左右孩子了，所以不行

中序是先把左子树干掉，再把自己干掉，自己没了就找不到右孩子了，也不行

后序是先把左右子树干掉，在释放自己，刚好符合我们的要求，所以就用后续

代码如下：

// 二叉树销毁
void BinaryTreeDestory(BTNode** root)//传二级是为了把root置空
{if (*root == nullptr)return;BinaryTreeDestory(&(*root)->_left);BinaryTreeDestory(&(*root)->_right);free(*root);*root = nullptr;
}

感谢大家观看！！！