1.11盛最多水的容器

参考：力扣题目链接；题解

1.1.题目

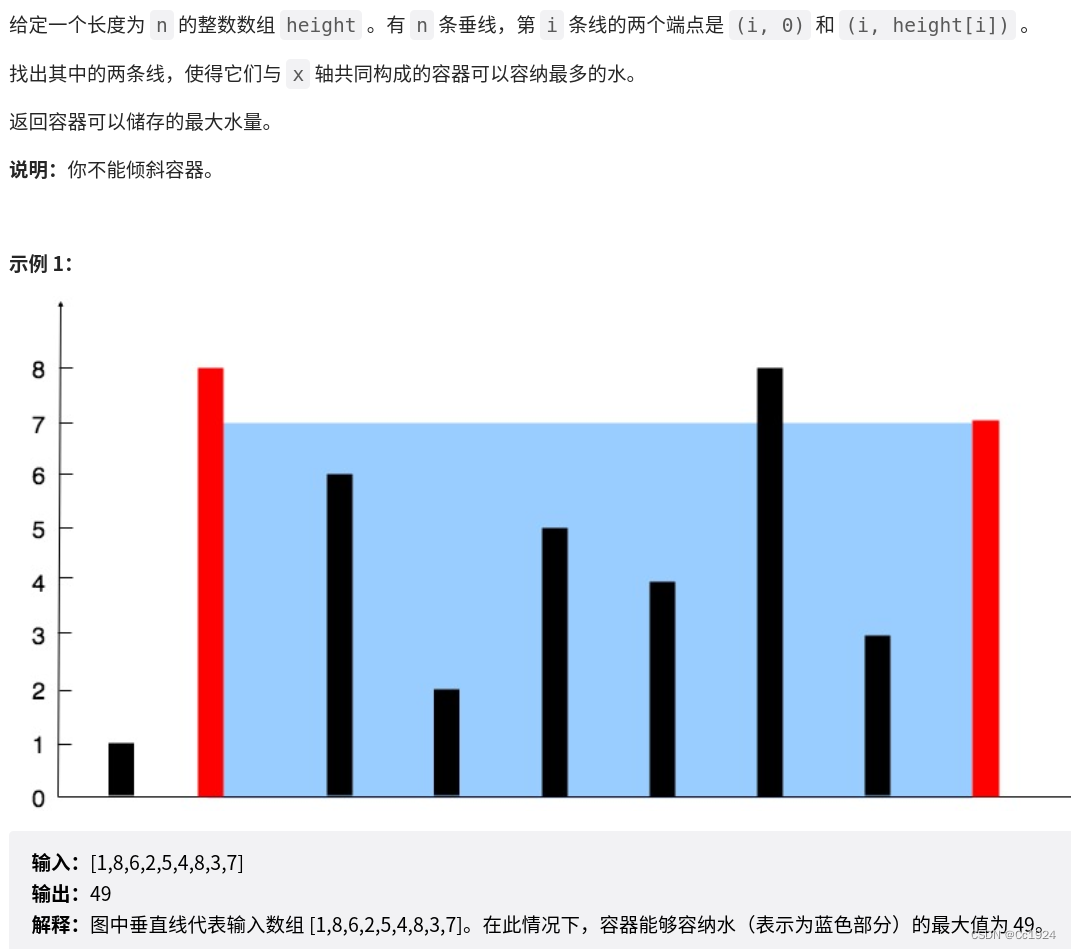
在这里插入图片描述

1.2.解答

1.2.1.题解

这道题目可以使用双指针来求解，其中参考题解的解释已经非常详细了，直接摘录如下：

在这里插入图片描述

1.2.2.自己对参考题解的进一步解释

假设这个容器如下图所示：
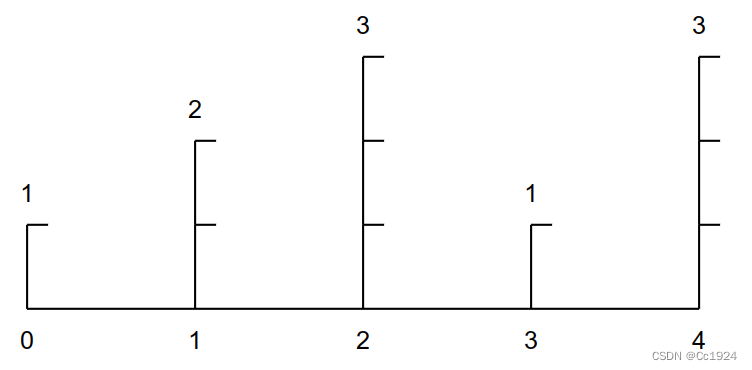
在这里插入图片描述

那么按照参考题解的做法，一开始左右边界是包含整个数组的。这里假设数组长度是n，然后数组中不包含的长度是i。那么我们想做的就是i从0开始遍历到n，数组的长度n-i也就是从n减小到0，然后我们寻找最大的面积。

1.i = 0，数组长度n-i = n
此时就是整个数组的长度，我们可以直接计算面积S_0 = min(num[0], num[4]) * (4 - 0)

2.i=1，数组长度n-i = n-1

此时我们必须要移动数组的边界了。按照参考题解的讲解，如果此时我们保持左边界left = 0不动，去移动右边界的话，那么不管右边界移动到什么位置，也就是不管数组长度是n/n-1/n-2/....，结果肯定都是小于S_0的。也就是说只要是以left = 0作为左边界，那么不管数组长度是多少，结果都小于之前我们已经做过的计算S_0。

因此当我们从当前的位置缩减数组长度的时候，一定不能把left=0仍然作为左边界了，所以只能把左边界右移，然后得到面积S_1 = min(num[1], num[4]) * (4-1)。

3.i=2，数组长度n-i = n-2

此时我们又要移动数组的边界。按照参考题解的讲解，如果此时我们保持左边界left = 1不动，去移动右边界的话，那么不管右边界移动到什么位置，也就是不管数组长度是n-1/n-2/n-3/...，结果肯定都是小于S_1的。也就是说只要是以left = 1作为左边界，那么不管数组长度是多少，结果都小于之前我们已经做过的计算S_1。

因此当我们从当前的位置缩减数组长度的时候，一定不能把left=1仍然作为左边界了，所以只能把左边界右移，然后得到面积S_2 = min(num[2], num[4]) * (4-2)。

疑问：但是这个时候自己的疑问就是，在数组长度是n-2的时候，如下图所示，我们可以选择左右边界为0-2、1-3、2-4，此时选择了2-4，并没有比较它和0-2、1-3两个数组的面积谁更大，怎么就能确定他是长度为n-2的所有数组中面积最大的呢？

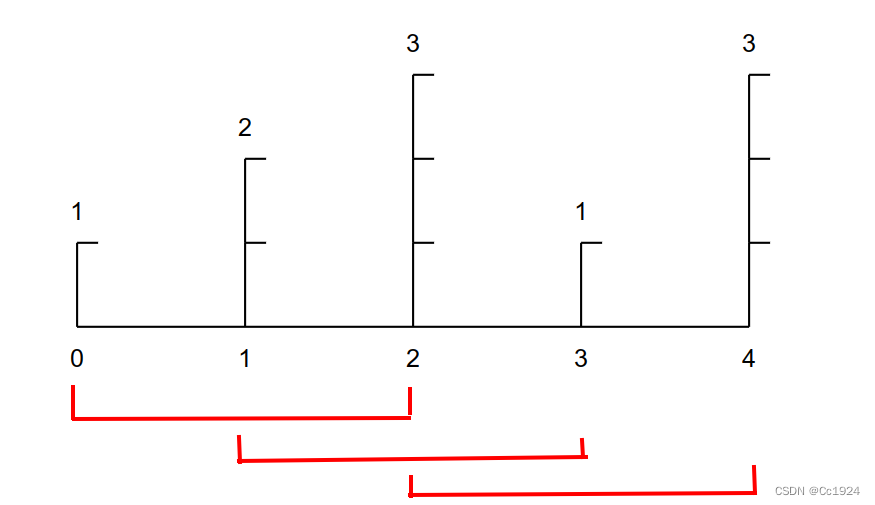
在这里插入图片描述

解答：实际上，确实无法判断2-4就是长度为n-2的数组中面积最大的。但是我们并不是要计算每个长度的数组中面积最大的，而是一直在判断所有长度的数组中面积最大的。

比如左右边界为0-2：此时是0为左边界，但是前面第2步移动窗口的时候我们已经证明，只要是以0为左边界，不管数组长度是多少，结果都小于我们已经计算的S_0。而S_0已经被用于统计是否是所有长度的数组中面积最大的了。所以在最终最大面积的结果中，一定可以保证S(0-2) <= S_0 = S(0-4) <= max_result。所以尽管我们不能确定0-2的面积和2-4的面积谁大谁小，但是我们可以确定最终的最大面积中，一定不包括0-2这个结果。所以在选择长度为n-2的数组时，不考虑0-2这个数组对最后我们求解最大面积没有影响。
再比如左右边界为1-3：此时是1为左边界。但是前面第3步移动窗口的时候我们已经证明，只要是以1为左边界，不管数组长度是多少，结果都小于我们已经计算的S_1。而S_1已经被用于统计是否是所有长度的数组中面积最大的了。所以在最终最大面积的结果中，一定可以保证S(1-3) <= S_1 = S(1-4) <= max_result。所以尽管我们不能确定1-3的面积和2-4的面积谁大谁小，但是我们可以确定最终的最大面积中，一定不包含1-3这个结果。所以在选择长度为n-2的数组时，不考虑1-3这个数组对最后我们求解最大面积没有影响。

经过上面的解释可以发现，之前移动数组的时候，移动了那个边界，就把以它为边界的所有其他数组的可能性都包括了，所以最后只需要移动左右边界就可以求得最优的解。

最后给出代码如下，使用双指针代码其实很简单，关键在于理解为什么使用双指针可以得到最优解。

int maxArea(vector<int> &height)
{int left = 0;int right = height.size() - 1;int result = 0;while(left < right){// 计算此次的面积int s = min(height[left], height[right]) * (right - left);// 和最大面积比较，更新最大面积result = max(s, result);// 移动短板if(height[left] <= height[right])left++;elseright--;}return result;
}