反向传播
弄一个简单点的,两层的神经网络:
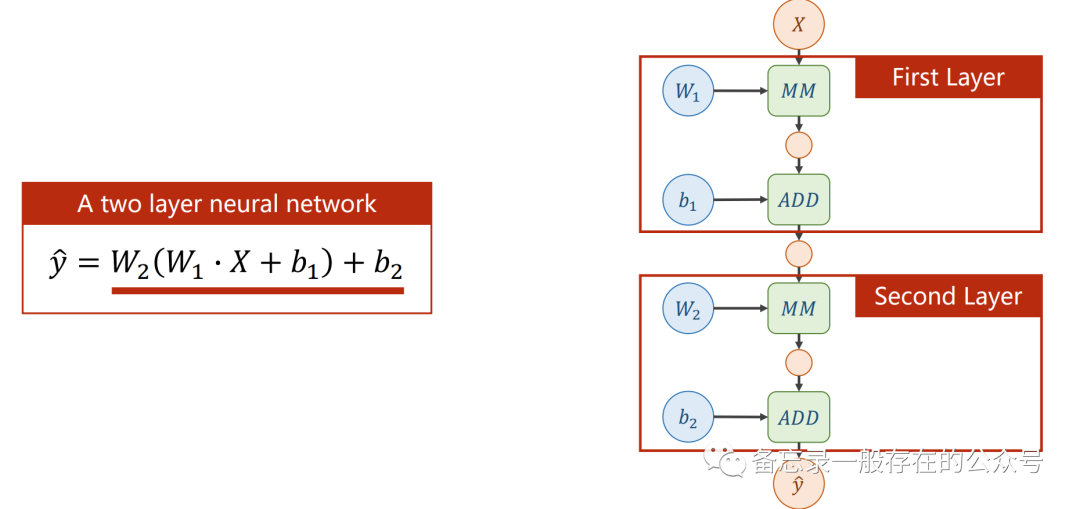
加入激活函数:(不加激活函数的神经网络就是一个线性回归模型)

用到的损失函数:
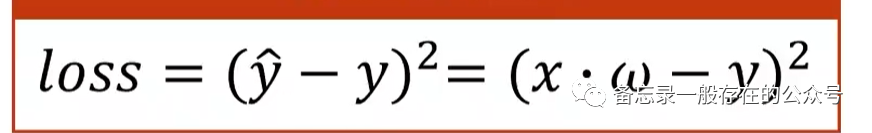
pytorch里面的数据存储:tensor,它可以存标量、向量、矩阵、高维度数据等。
所有的数值都保存在tensor里面,data和grad分别用来保存权重本身的值和损失函数对权重的导数。
定义好了tensor,就可以建立计算图了。
代码:
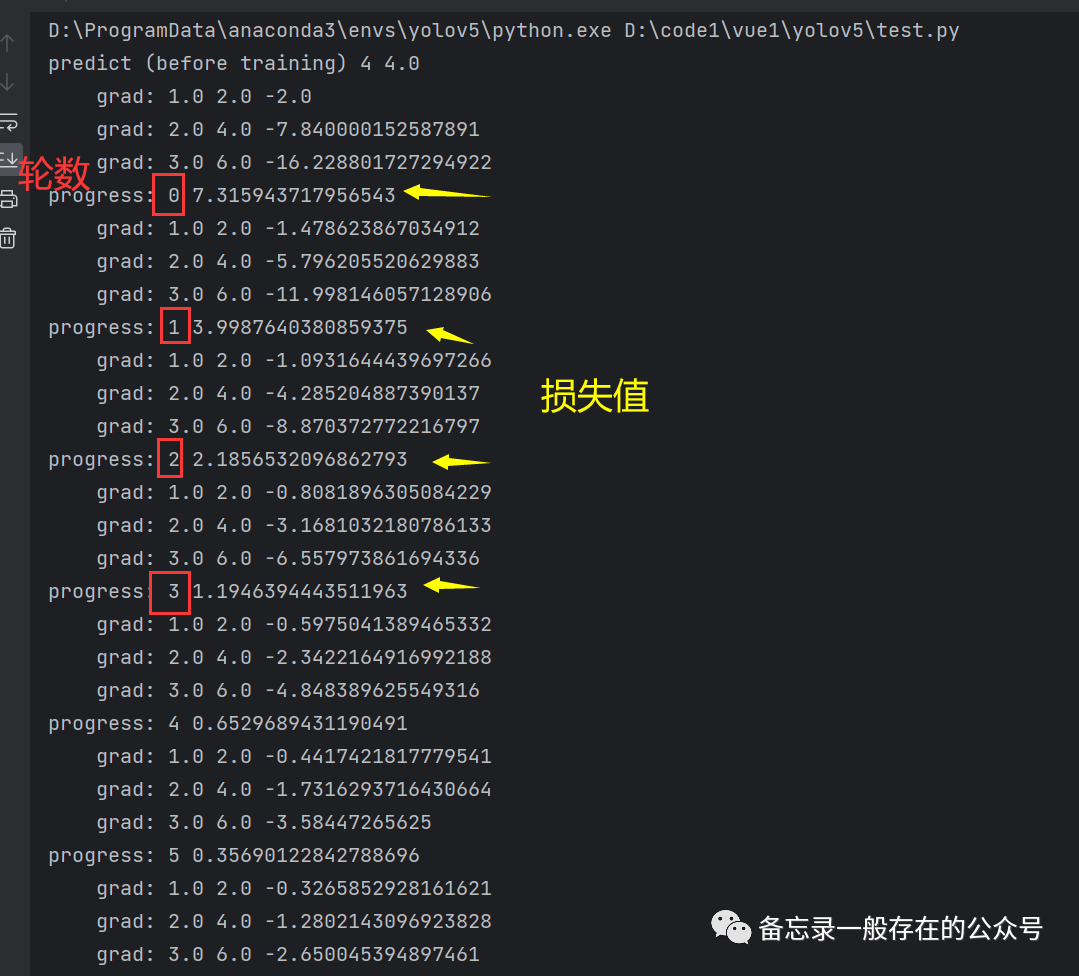
import torchx_data = [1.0, 2.0, 3.0] #构建数据集y_data = [2.0, 4.0, 6.0] #(1.0,2.0)是一个样本,(2.0,4.0)是一个样本,以此类推w = torch.tensor([1.0]) # w的初值为1.0,一定要用中括号给他括起来w.requires_grad = True # 需要计算梯度。默认的tensor创建后是不需要计算梯度的,所以在计算的时候,构建的计算图里面不会保留计算关于当前的w的梯度,只有在设置为true的时候才会计算def forward(x):return x * w # w是一个Tensor,所以当它遇到乘法运算的时候,这个运算符实际上已经被重载了,它要进行的就是tensor与tensor之间的数乘#重载就是说一个运算符有多个功能,但是作用的对象不同#构建计算图def loss(x, y): #计算损失y_pred = forward(x)return (y_pred - y) ** 2print("predict (before training)", 4, forward(4).item())for epoch in range(100): #数据准备,训练100轮for x, y in zip(x_data, y_data): #随机梯度下降,每次把(x_data,y_data) zip 成一个样本l = loss(x, y) # l是一个张量,tensor主要是在建立计算图 forward, compute the loss(前馈过程,计算Loss)l.backward() # backward,compute grad for Tensor whose requires_grad set to True(反馈过程,调用backward函数,自动计算所有需要w计算梯度的对应的值)#计算出来的梯度会保存到前边设置的w中(就是“w = torch.tensor([1.0])”这一行)#存到w中了之后,这个计算图就被释放了。只要一做backward,计算图就被释放了,准备下一次的图#在下一次的loss中会创建出新的计算图print('\tgrad:', x, y, w.grad.item()) #item,标量w.data = w.data - 0.01 * w.grad.data # 权重更新时,注意grad也是一个tensor(取所有张量的data来进行计算是不会建立计算图的)w.grad.data.zero_() # after update, remember set the grad to zero (把权重里面的梯度数据全部清零)print('progress:', epoch, l.item()) # 取出loss使用l.item,不要直接使用l(l是tensor会构建计算图)print("predict (after training)", 4, forward(4).item())
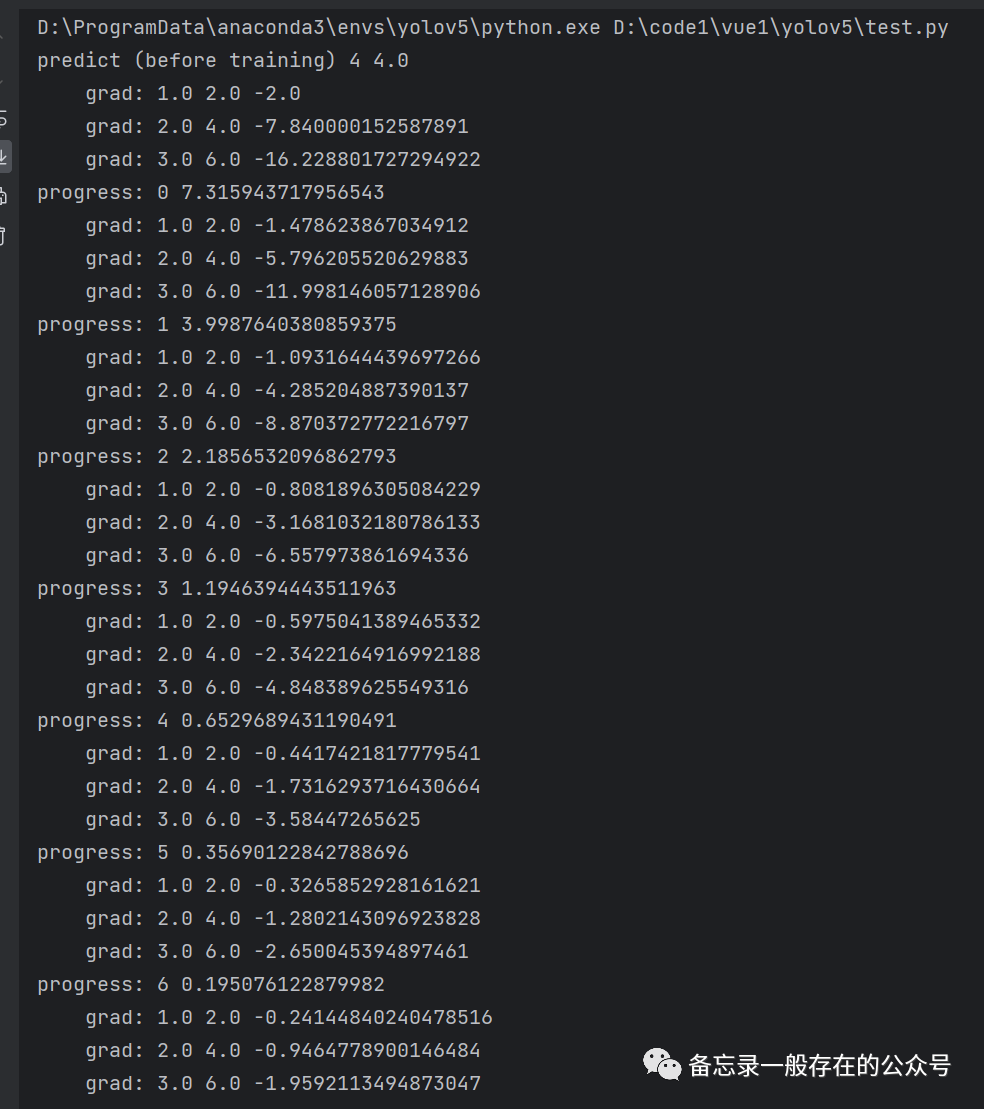
练习:输入为二次的线性模型(如下图)
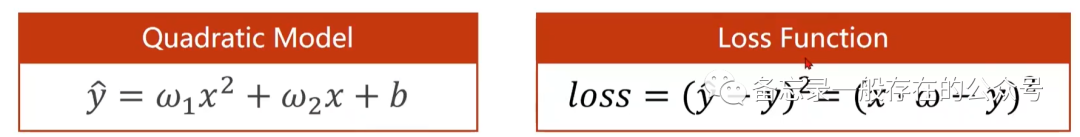
import numpy as npimport matplotlib.pyplot as pltimport torchx_data = [1.0,2.0,3.0]y_data = [2.0,4.0,6.0]w1 = torch.Tensor([1.0])#初始权值w1.requires_grad = True#计算梯度,默认是不计算的w2 = torch.Tensor([1.0])w2.requires_grad = Trueb = torch.Tensor([1.0])b.requires_grad = Truedef forward(x):return w1 * x**2 + w2 * x + bdef loss(x,y):#构建计算图y_pred = forward(x)return (y_pred-y) **2print('Predict (befortraining)',4,forward(4))for epoch in range(100):l = loss(1, 2)#为了在for循环之前定义l,以便之后的输出,无实际意义for x,y in zip(x_data,y_data):l = loss(x, y)l.backward()print('\tgrad:',x,y,w1.grad.item(),w2.grad.item(),b.grad.item())w1.data = w1.data - 0.01*w1.grad.data #注意这里的grad是一个tensor,所以要取他的dataw2.data = w2.data - 0.01 * w2.grad.datab.data = b.data - 0.01 * b.grad.dataw1.grad.data.zero_() #释放之前计算的梯度w2.grad.data.zero_()b.grad.data.zero_()print('Epoch:',epoch,l.item())print('Predict(after training)',4,forward(4).item())
用pytorch实现线性回归
四大步骤:准备数据集,设计模型,计算损失和定义优化器,训练周期。
代码:
import torch# prepare dataset# x,y是矩阵,3行1列 也就是说总共有3个数据,每个数据只有1个特征x_data = torch.tensor([[1.0], [2.0], [3.0]]) #1.0是第一行,2.0是第二行,3.0是第三行。3×1的矩阵y_data = torch.tensor([[2.0], [4.0], [6.0]])# design model using classclass LinearModel(torch.nn.Module): #把模型定义为一个类(LinearModel),所有的模型都需要去继承自Module,因为Module这个类里面有很多的方法是需要在后续的模型训练中会用到的#这个类里面最少需要实现两个函数,第一个就是initial函数,也就是构造函数嘛;第二个就是forward函数(必须叫forward)def __init__(self): #构造函数是用来在初始化对象的时候需要默认调用的函数super(LinearModel, self).__init__() #调用父类的构造,这步必须有# (1,1)是指输入x和输出y的特征维度,这里数据集中的x和y的特征都是1维的# 该线性层需要学习的参数是w和b 获取w/b的方式分别是~linear.weight/linear.biasself.linear = torch.nn.Linear(1, 1) #使用torch.nn.Linear,这个是pytorch里面的类,类里面加括号,实际上就是在构造对象,包含了w(权重)和b(偏置)#此处的Linear也是继承自Module的,所以它能够自动的进行反向传播;linear是对象;nn是缩写:Neural Network(神经网络)def forward(self, x): #forward是在进行前馈的过程中所要执行的计算。这里没有backward,因为用Module构造的出来的对象,这种对象会自动的根据计算图去实现backward的过程y_pred = self.linear(x) #求y^,函数后面加括号,可调用对象;x是3×1的矩阵return y_predmodel = LinearModel() #实例化# construct loss and optimizer# criterion = torch.nn.MSELoss(size_average = False) #size_average默认是false,不求均值criterion = torch.nn.MSELoss(reduction='sum') #构造损失函数。MSELoss也是继承自nn.Moduleoptimizer = torch.optim.SGD(model.parameters(), lr=0.01) # model.parameters()自动完成参数的初始化操作;定义优化器#优化器不会构建计算图;parameters会检查Module里面的所有成员,如果成员里面有相应的权重,就会把这些加到要训练的参数集合上# training cycle forward, backward, updatefor epoch in range(1000):y_pred = model(x_data) # forward:predict 前馈里面算y^,把x_data算进去loss = criterion(y_pred, y_data) # forward: loss 算损失print(epoch, loss.item()) #loss是标量optimizer.zero_grad() # the grad computer by .backward() will be accumulated. so before backward, remember set the grad to zero#梯度归零loss.backward() # backward: autograd,自动计算梯度optimizer.step() # update 参数,即更新w和b的值;根据所有参数包含的梯度和学习率自动更新print('w = ', model.linear.weight.item()) #不加item的话,就是一个矩阵print('b = ', model.linear.bias.item())#测试模型x_test = torch.tensor([[4.0]]) #1×1y_test = model(x_test)print('y_pred = ', y_test.data) #输出也是1×1
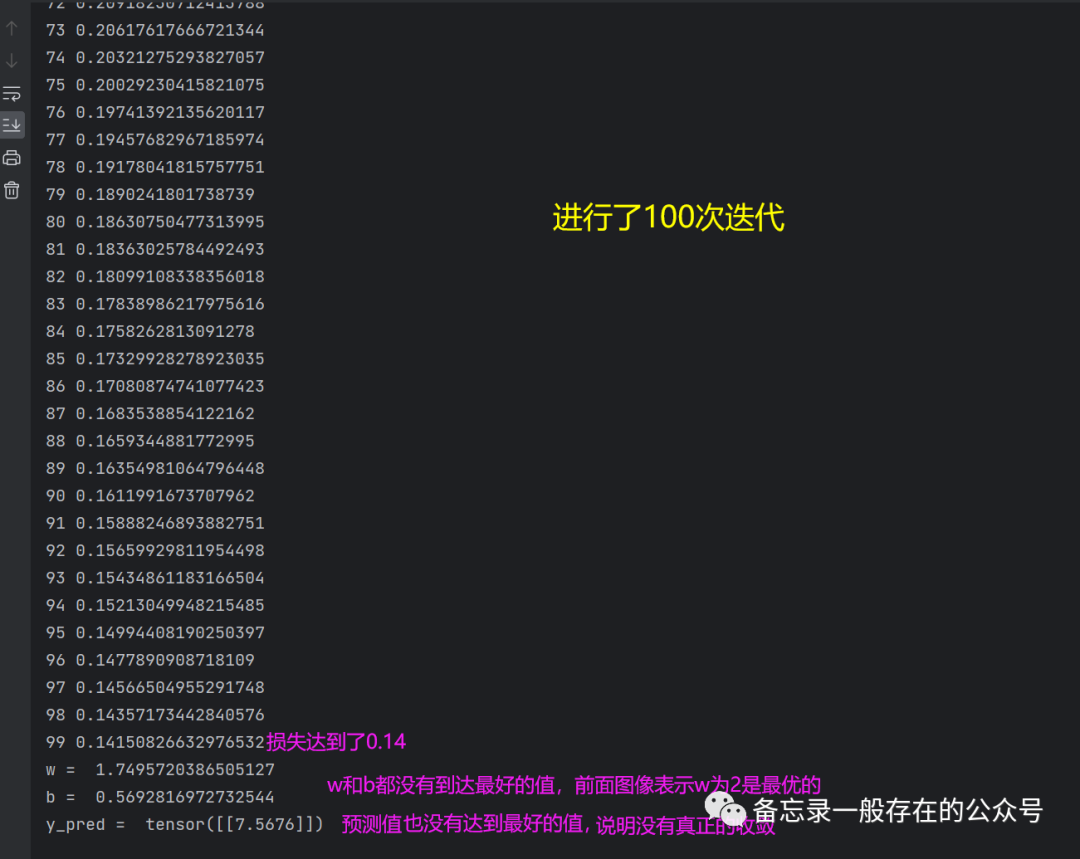
当我们迭代1000次,得到的结果就会好一些:
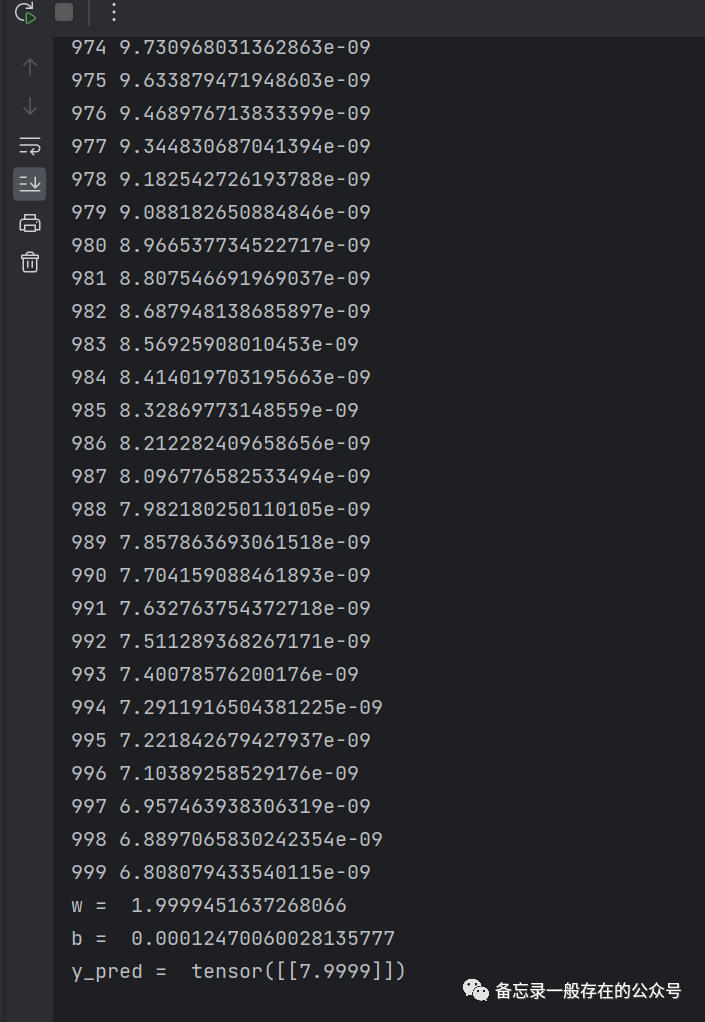
同时,也要注意到这是有风险的。增加训练的轮数,对于训练的损失不断减少,测试集上的损失可能会少着少着就又回升了,说明过拟合了。
在真正的训练过程中,不仅要关注训练集上的损失,也要关注测试集上的损失。
不同的优化器可以去尝试,产生的损失会有差别: