目录

一，斜率优化

1，斜率优化原理

2，凸包和斜率计算

3，实战

黑暗爆炸 - 4709 柠檬

二，else

力扣 644. 子数组最大平均数 II（最大子段和+二分）

​力扣 646. 最长数对链

 力扣 1235. 规划兼职工作

 力扣 1340. 跳跃游戏 V

 力扣 1696. 跳跃游戏 VI（不能用备忘录）

 力扣 1335. 工作计划的最低难度

---

本文列举的都是不满足数列DP基础中的通项公式的问题。

一，斜率优化

有一类单数列DP问题，用公式形如dp(i) = max{dp(j)+f(i,j) | j<i}，相比简单的单数列DP问题，这个递推式的时间复杂度显然更高。

如果f函数满足一定的条件，则可以使用斜率优化加快速度。

1，斜率优化原理

如果，递推公式可以表示成dp(i) = max{dp(j) + f(i,j) | j<i且...}

其中f(i,j)可以表示成g1(i)g2(j)+g3(i)+g4(j)，其中g1,g2,g3,g4是4个函数，且g2具有单调性

那么，递推公式可以化成dp(i)=g3(i)+max{dp(j)+g4(j) + g1(i)g2(j)}

于是问题转化为，在一个点集中，求y-kx的最大值（或最小值），其中x是g2(j)，y是dp(j)+g4(j)，k是-g1(i)

而快速求解这个最值的方法就是凸包+二分

2，凸包、y-kx最值计算

凸包

3，实战

黑暗爆炸 - 4709 柠檬

Description

Flute 很喜欢柠檬。它准备了一串用树枝串起来的贝壳，打算用一种魔法把贝壳变成柠檬。贝壳一共有 N (1 ≤ N ≤ 100,000) 只，按顺序串在树枝上。为了方便，我们从左到右给贝壳编号 1..N。每只贝壳的大小不一定相同，贝壳 i 的大小为 si(1 ≤ si ≤10,000)。变柠檬的魔法要求，Flute 每次从树枝一端取下一小段连续的贝壳，并选择一种贝壳的大小 s0。如果 这一小段贝壳中 大小为 s0 的贝壳有 t 只，那么魔法可以把这一小段贝壳变成 s0t^2 只柠檬。Flute 可以取任意多次贝壳，直到树枝上的贝壳被全部取完。各个小段中，Flute 选择的贝壳大小 s0 可以不同。而最终 Flute 得到的柠檬数，就是所有小段柠檬数的总和。Flute 想知道，它最多能用这一串贝壳变出多少柠檬。请你帮忙解决这个问题。

Input

第 1 行：一个整数，表示 N。

第 2 .. N + 1 行：每行一个整数，第 i + 1 行表示 si。

Output

仅一个整数，表示 Flute 最多能得到的柠檬数。

Sample

Inputcopy	Outputcopy
5 2 2 5 2 3	21 //Flute 先从左端取下 4 只贝壳，它们的大小为 2, 2, 5, 2。选择 s0 = 2，那么这一段 里有 3 只大小为 s0 的贝壳，通过魔法可以得到 2×3^2 = 18 只柠檬。再从右端取下最后一 只贝壳，通过魔法可以得到 1×3^1 = 3 只柠檬。总共可以得到 18 + 3 = 21 只柠檬。没有 比这更优的方案了。

思路：

dp[i]表示前i个贝壳可以变成多少柠檬，1<=i<=n，dp[n]就是本题答案。

arr[i]表示输入的数据，1<=i<=n

num[i]表示arr的前i个数中，等于arr[i]的有多少个（至少1个）

递推式：dp[i] = max{dp[j-1] + arr[i] * (num[i]-num[j]+1)^2 | 1<=j<=i, arr[j]==arr[i]}

dp[0]=0

斜率优化：

dp[i]=arr[i]* (num[i]+1)^2 + max{dp[j-1] + arr[j] * num[j] * (num[j]-2num[i]-2) | 1<=j<=i, arr[j]==arr[i]}

即dp[i]=arr[i]* (num[i]+1)^2 + max{dp[j-1] + arr[j] * num[j] * (num[j]-2) -2num[i] * arr[j] * num[j] | 1<=j<=i, arr[j]==arr[i]}

这就是求y-kx的最大值，y=dp[j-1] + arr[j] * num[j] * (num[j]-2), k=2num[i], x=arr[j] * num[j]

虽然arr[j] * num[j]并不是关于j的单调函数，但是在{j|arr[j]==arr[i]}这个生成空间中，是单调的。

二，else

力扣 644. 子数组最大平均数 II（最大子段和+二分）

给你一个包含 n 个整数的数组 nums ，和一个整数 k 。

请你找出 长度大于等于 k 且含最大平均值的连续子数组。并输出这个最大平均值。任何计算误差小于 10-5 的结果都将被视为正确答案。

示例 1：

输入：nums = [1,12,-5,-6,50,3], k = 4
输出：12.75000
解释：
- 当长度为 4 的时候，连续子数组平均值分别为 [0.5, 12.75, 10.5] ，其中最大平均值是 12.75 。
- 当长度为 5 的时候，连续子数组平均值分别为 [10.4, 10.8] ，其中最大平均值是 10.8 。
- 当长度为 6 的时候，连续子数组平均值分别为 [9.16667] ，其中最大平均值是 9.16667 。
当取长度为 4 的子数组（即，子数组 [12, -5, -6, 50]）的时候，可以得到最大的连续子数组平均值 12.75 ，所以返回 12.75 。
根据题目要求，无需考虑长度小于 4 的子数组。
示例 2：

输入：nums = [5], k = 1
输出：5.00000
 

提示：

n == nums.length
1 <= k <= n <= 104
-104 <= nums[i] <= 104

思路：二分+DP

//获取列表中最大值
template<typename T>
T GetMax(const vector<T> &v)
{T ans = v[0];for (int i = 1; i < v.size(); i++)ans = max(ans, v[i]);return ans;
}
//获取列表中最小值
template<typename T>
T GetMin(const vector<T> &v)
{T ans = v[0];for (int i = 1; i < v.size(); i++)ans = min(ans, v[i]);return ans;
}
//求以每个元素开头的最大子段和
template<typename T>
vector<T> maxSubArrayFromEver(const vector<T> &v)
{vector<T>ans = v;for (int i = v.size() - 2; i >= 0; i--) {if (ans[i + 1] >= 0)ans[i] += ans[i + 1];}return ans;
}
class Solution {
public:bool ok(const vector<int> &anums, int k, double avg){vector<double>nums(anums.size());for (int i = 0; i < nums.size(); i++)nums[i] = anums[i] - avg;auto msub = maxSubArrayFromEver(nums);double s = 0;for (int i = 0; i < k; i++)s += nums[i];for (int i = k - 1; i < nums.size(); i++) {if (i >= k)s += nums[i] - nums[i - k];if (s >= 0)return true;if (i < nums.size() - 1 && s + msub[i + 1] >= 0)return true;}return false;}double findMaxAverage(vector<int>& nums, int k) {double amin = GetMin(nums);double amax = GetMax(nums);while (amax - amin >= 0.00001) {double mid = (amax + amin) / 2;if (ok(nums, k, mid))amin = mid;else amax = mid;}return amin;}
};

​力扣 646. 最长数对链

题目：

给出 n 个数对。 在每一个数对中，第一个数字总是比第二个数字小。

现在，我们定义一种跟随关系，当且仅当 b < c 时，数对(c, d) 才可以跟在 (a, b) 后面。我们用这种形式来构造一个数对链。

给定一个对数集合，找出能够形成的最长数对链的长度。你不需要用到所有的数对，你可以以任何顺序选择其中的一些数对来构造。

示例 :

输入: [[1,2], [2,3], [3,4]]
输出: 2
解释: 最长的数对链是 [1,2] -> [3,4]
注意：

给出数对的个数在 [1, 1000] 范围内。

分析：

动态规划。

因为数据量只有1000，所以直接写个简单的O(n*n)的时间的算法即可

代码：

bool cmp(vector<int> it1,vector<int> it2)
{return it1[1]<it2[1];
}class Solution {
public:int findLongestChain(vector<vector<int>>& pairs) {    int res=0;vector<vector<int>>ans;vector<int>temp;ans.clear();        sort(pairs.begin(),pairs.end(),cmp);for(auto it=pairs.begin();it!=pairs.end();it++){temp.clear();temp.insert(temp.end(),(*it)[1]);temp.insert(temp.end(),1);for(auto it2=ans.begin();it2!=ans.end();it2++){if((*it)[0]>(*it2)[0] && temp[1]<(*it2)[1]+1){temp[1]=(*it2)[1]+1;}}ans.insert(ans.end(),temp);if(res<temp[1]){res=temp[1];}}return res;}
};

还有一种贪心的算法：

以第二个数为第一关键字，第一个数为第二个关键字，进行排序。

 力扣 1235. 规划兼职工作

你打算利用空闲时间来做兼职工作赚些零花钱。

这里有 n 份兼职工作，每份工作预计从 startTime[i] 开始到 endTime[i] 结束，报酬为 profit[i]。

给你一份兼职工作表，包含开始时间 startTime，结束时间 endTime 和预计报酬 profit 三个数组，请你计算并返回可以获得的最大报酬。

注意，时间上出现重叠的 2 份工作不能同时进行。

如果你选择的工作在时间 X 结束，那么你可以立刻进行在时间 X 开始的下一份工作。

示例 1：

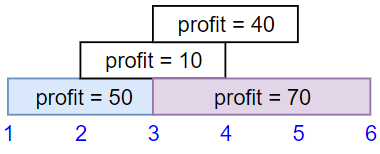
输入：startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
输出：120
解释：
我们选出第 1 份和第 4 份工作， 
时间范围是 [1-3]+[3-6]，共获得报酬 120 = 50 + 70。

示例 2：

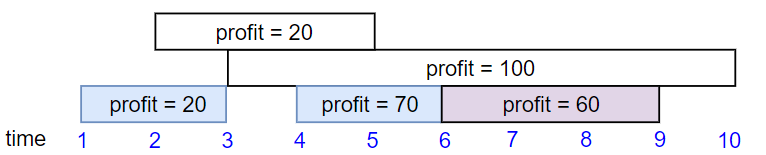
输入：startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
输出：150
解释：
我们选择第 1，4，5 份工作。 
共获得报酬 150 = 20 + 70 + 60。

示例 3：

输入：startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
输出：6

提示：

• 1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
• 1 <= startTime[i] < endTime[i] <= 10^9
• 1 <= profit[i] <= 10^4

//拓展数据域，加上id
template<typename T>
vector<pair<T, int>>expand(vector<T>v)
{vector<pair<T, int>>ans;ans.resize(v.size());for (int i = 0; i < v.size(); i++)ans[i].first = v[i], ans[i].second = i;return ans;
}
//提取pair数组的second
template<typename T1, typename T2>
vector<T2> fdraw2(vector<pair<T1, T2>>v)
{vector<T2>ans(v.size());for (int i = 0; i < v.size(); i++)ans[i] = v[i].second;return ans;
}
//给vector拓展，加上id并排序
template<typename T>
bool cmp(pair<T, int> x, pair<T, int> y)
{if (x.first == y.first)return x.second < y.second;return x.first < y.first;
}
template<typename T>
vector<pair<T, int>> sortWithId(vector<T>v)
{vector<pair<T, int>>ans = expand(v);sort(ans.begin(), ans.end(), cmp<T>);return ans;
}
//排序后数组中的每个数的原ID，输入8 5 6 7，输出1 2 3 0，也可以直接求逆置换
template<typename T>
vector<int> sortId(vector<T>v)
{return fdraw2(sortWithId(v));
}
//2个vector拼接起来
template<typename T>
vector<T> join(const vector<T>& v1, const vector<T>& v2)
{vector<T>ans(v1.size() + v2.size());copy(v1.begin(), v1.end(), ans.begin());copy(v2.begin(), v2.end(), ans.begin() + v1.size());return ans;
}
//把id数组转化为对应的数v[id]
template<typename T>
vector<T> fgetNumFromId(vector<T>& v, vector<int>id)
{vector<T>ans;ans.resize(id.size());for (int i = 0; i < id.size(); i++)ans[i] = (id[i] >= 0 && id[i] < v.size()) ? v[id[i]] : -1;return ans;
}
class Solution {
public:map<int,int> div(vector<int>v){sort(v.begin(),v.end());map<int, int>ans;for (int i = 1; i < v.size(); i++)if (v[i] != v[i - 1])ans[v[i]] = ans[v[i - 1]] + 1;return ans;}int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {vector<int>v = join(startTime,endTime);map<int, int> m = div(v);v = sortId(endTime);vector<int> id = fgetNumFromId(endTime, v);map<int, int>mans;mans[m[id[0]]] = profit[v[0]];for (int i = 1; i < v.size(); i++) {for (int j = m[id[i - 1]] + 1; j < m[id[i]]; j++)mans[j] = mans[m[id[i - 1]]];mans[m[id[i]]] = max(max(profit[v[i]] + mans[m[startTime[v[i]]]], mans[m[id[i - 1]]]), mans[m[id[i]]]);}return mans[m[id[v.size() - 1]]];}
};

 力扣 1340. 跳跃游戏 V

给你一个整数数组 arr 和一个整数 d 。每一步你可以从下标 i 跳到：

• i + x ，其中 i + x < arr.length 且 0 < x <= d 。
• i - x ，其中 i - x >= 0 且 0 < x <= d 。

除此以外，你从下标 i 跳到下标 j 需要满足：arr[i] > arr[j] 且 arr[i] > arr[k] ，其中下标 k 是所有 i 到 j 之间的数字（更正式的，min(i, j) < k < max(i, j)）。

你可以选择数组的任意下标开始跳跃。请你返回你 最多 可以访问多少个下标。

请注意，任何时刻你都不能跳到数组的外面。

示例 1：

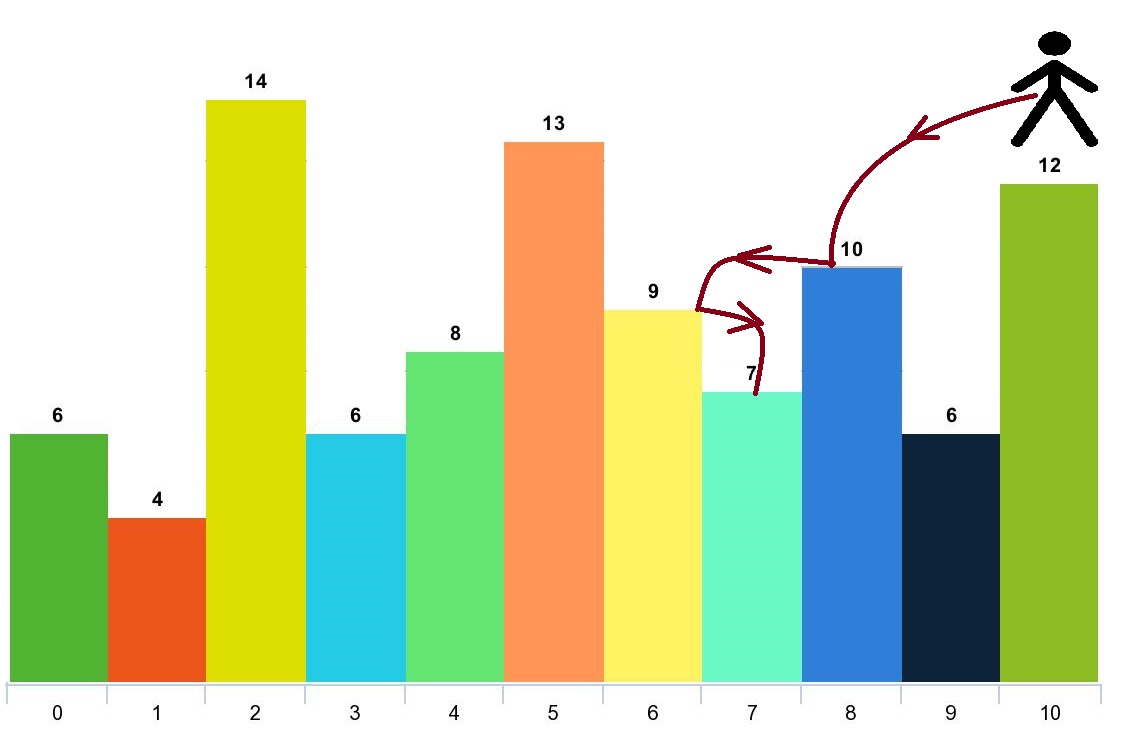
输入：arr = [6,4,14,6,8,13,9,7,10,6,12], d = 2
输出：4
解释：你可以从下标 10 出发，然后如上图依次经过 10 --> 8 --> 6 --> 7 。
注意，如果你从下标 6 开始，你只能跳到下标 7 处。你不能跳到下标 5 处因为 13 > 9 。你也不能跳到下标 4 处，因为下标 5 在下标 4 和 6 之间且 13 > 9 。
类似的，你不能从下标 3 处跳到下标 2 或者下标 1 处。

示例 2：

输入：arr = [3,3,3,3,3], d = 3
输出：1
解释：你可以从任意下标处开始且你永远无法跳到任何其他坐标。

示例 3：

输入：arr = [7,6,5,4,3,2,1], d = 1
输出：7
解释：从下标 0 处开始，你可以按照数值从大到小，访问所有的下标。

示例 4：

输入：arr = [7,1,7,1,7,1], d = 2
输出：2

示例 5：

输入：arr = [66], d = 1
输出：1

提示：

• 1 <= arr.length <= 1000
• 1 <= arr[i] <= 10^5
• 1 <= d <= arr.length

class Solution {
public:map<int, int>m;int dp(vector<int>& arr, int d, int id){if (m[id])return m[id];int ans = 1;for (int i = id - 1; i >= id - d; i--) {if (i < 0 || arr[i] >= arr[id])break;ans = max(ans, dp(arr, d, i) + 1);}for (int i = id + 1; i <= id + d; i++) {if (i >= arr.size() || arr[i] >= arr[id])break;ans = max(ans, dp(arr, d, i) + 1);}return m[id] = ans;}int maxJumps(vector<int>& arr, int d) {int ans = 0;for (int i = 0; i < arr.size(); i++)ans = max(ans, dp(arr, d, i));return ans;}
};

 力扣 1696. 跳跃游戏 VI（不能用备忘录）

给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。

一开始你在下标 0 处。每一步，你最多可以往前跳 k 步，但你不能跳出数组的边界。也就是说，你可以从下标 i 跳到 [i + 1， min(n - 1, i + k)] 包含 两个端点的任意位置。

你的目标是到达数组最后一个位置（下标为 n - 1 ），你的 得分 为经过的所有数字之和。

请你返回你能得到的 最大得分 。

示例 1：

输入：nums = [1,-1,-2,4,-7,3], k = 2
输出：7
解释：你可以选择子序列 [1,-1,4,3] （上面加粗的数字），和为 7 。

示例 2：

输入：nums = [10,-5,-2,4,0,3], k = 3
输出：17
解释：你可以选择子序列 [10,4,3] （上面加粗数字），和为 17 。

示例 3：

输入：nums = [1,-5,-20,4,-1,3,-6,-3], k = 2
输出：0

提示：

•  1 <= nums.length, k <= 105
• -104 <= nums[i] <= 104

因为性能的问题，不能只用递推式，还需要优先队列来优化，所以要按照严格的顺序来dp，即非备忘录写法。

map<int, int>m;
class Solution {
public:struct cmp {bool operator()(int x, int y) {return m[x] < m[y];}};priority_queue<int, vector<int>, cmp>q;void dp(vector<int>& nums, int k, int id) {if (id == nums.size() - 1) {q.push(id);m[id] = nums[id];return;}int x = q.top();while (x - id > k)q.pop(), x = q.top();m[id] = nums[id] + m[x];q.push(id);}int maxResult(vector<int>& nums, int k) {for (int i = nums.size() - 1; i >= 0; i--)dp(nums, k, i);return m[0];}
};

 力扣 1335. 工作计划的最低难度

你需要制定一份 d 天的工作计划表。工作之间存在依赖，要想执行第 i 项工作，你必须完成全部 j 项工作（ 0 <= j < i）。

你每天 至少 需要完成一项任务。工作计划的总难度是这 d 天每一天的难度之和，而一天的工作难度是当天应该完成工作的最大难度。

给你一个整数数组 jobDifficulty 和一个整数 d，分别代表工作难度和需要计划的天数。第 i 项工作的难度是 jobDifficulty[i]。

返回整个工作计划的 最小难度 。如果无法制定工作计划，则返回 -1 。

示例 1：

输入：jobDifficulty = [6,5,4,3,2,1], d = 2
输出：7
解释：第一天，您可以完成前 5 项工作，总难度 = 6.
第二天，您可以完成最后一项工作，总难度 = 1.
计划表的难度 = 6 + 1 = 7 
示例 2：

输入：jobDifficulty = [9,9,9], d = 4
输出：-1
解释：就算你每天完成一项工作，仍然有一天是空闲的，你无法制定一份能够满足既定工作时间的计划表。
示例 3：

输入：jobDifficulty = [1,1,1], d = 3
输出：3
解释：工作计划为每天一项工作，总难度为 3 。
示例 4：

输入：jobDifficulty = [7,1,7,1,7,1], d = 3
输出：15
示例 5：

输入：jobDifficulty = [11,111,22,222,33,333,44,444], d = 6
输出：843
 

提示：

1 <= jobDifficulty.length <= 300
0 <= jobDifficulty[i] <= 1000
1 <= d <= 10

class Solution {
public:map<int, map<int, int>>m;int dp(vector<int>& v, int id, int d){if (m[id][d])return m[id][d];if (d > id + 1)return 123456789;int ans = dp(v, id - 1, d - 1) + v[id];int x = v[id];for (int i = id - 1; i >= 0; i--) {x = max(x, v[i + 1]);ans = min(ans, dp(v, i, d-1) + x);}return m[id][d] = ans;}int minDifficulty(vector<int>& v, int d) {for (int i = 0; i < v.size(); i++) {v[i]++;m[i][1] = max(m[i - 1][1], v[i]);}int ans = dp(v, v.size() - 1, d);return ans == 123456789 ? -1 : ans - d;}
};