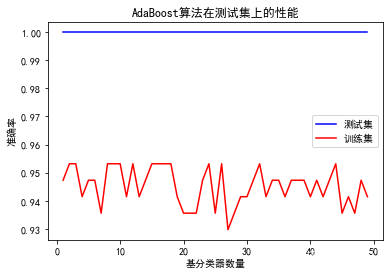
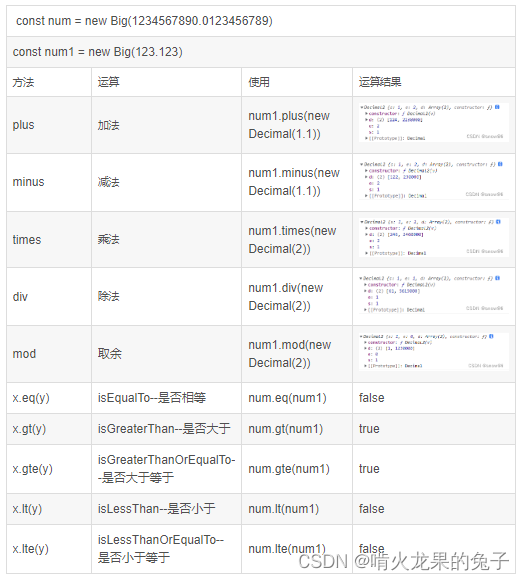
1. 数据分类

数据分类可以根据不同的度量水平进行分类，其中常见的分类方法包括定类、定序、定距和定比。

（1）定类（Nominal）：定类是最基本的数据分类方式，用于对数据进行无序的分类。在定类数据中，每个数据点被分配到一个独立的类别，但类别之间没有任何内在的顺序或大小关系。例如，性别（男、女）、国家/地区（中国、美国、英国）等都属于定类数据。

（2）定序（Ordinal）：定序是对数据进行有序分类的方式。在定序数据中，类别之间具有一定的顺序或大小关系，但差异的大小不能明确量化。常见的例子包括教育程度（小学、初中、高中、大学）、星级评定（一星级、二星级、三星级）等。

（3）定距（Interval）：定距是对数据进行有序分类，并且具有可量化的差异大小。在定距数据中，类别之间的差异是相等的，但没有绝对的零点。常见的例子包括温度（摄氏度、华氏度）、年份（2000年、2010年、2020年）等。

（4）定比（Ratio）：定比是对数据进行有序分类，并且具有可量化的差异大小，并且具有绝对的零点。在定比数据中，可以进行比例和比率的计算。常见的例子包括长度（厘米、英寸）、时间（秒、分钟、小时）等。

这些数据分类方法对于不同的数据分析和建模任务具有不同的应用。定类数据适用于标签、分类和计数等任务；定序数据适用于排序和排名等任务；定距数据适用于数值计算和统计分析等任务；定比数据适用于比例和比率的计算等任务。理解数据的分类方式可以帮助我们选择合适的分析方法和解释数据的含义。

2. 异常值分析

2.1 概述

异常值分析是数据分析的重要步骤之一，它旨在识别和处理数据中的异常值或离群值。异常值是指与其他观测值明显不同的数据点，它可能是由于测量误差、数据录入错误、实验异常或真实的极端情况所导致。

2.2 异常值分类

在异常值分析中，可以将异常值分为连续异常值、离散异常值和知识异常值。这些异常值的分类方式是根据其特征和产生原因进行划分的。

（1）连续异常值：连续异常值指的是在连续变量中出现的异常数值。这些异常值通常是数值上与其他观测值明显不同的数据点。例如，在身高数据中，如果出现一个明显超过平均身高的极端值，那么它可以被认为是连续异常值。

（2）离散异常值：离散异常值指的是在离散变量中出现的异常类别或取值。这些异常值与其他类别或取值明显不同，可能是由于数据输入错误或数据本身特殊性所导致。例如，在性别数据中，如果出现了一个不在"男"或"女"之间的异常类别，那么它可以被视为离散异常值。

（3）知识异常值：知识异常值是基于领域知识和业务经验进行判断的异常值。它们可能不符合统计上的异常标准，但根据专业知识和经验判断，这些值可能是异常的。例如，在医疗诊断中，根据医生的专业知识，某些医疗指标可能被认为是异常值，即使它们在统计上并不显著。

对于连续异常值和离散异常值，可以使用统计方法、可视化方法或领域知识来识别和处理。而对于知识异常值，需要依赖专业领域的知识和经验进行判断和处理。

在异常值分析中，同时考虑连续异常值、离散异常值和知识异常值，可以更全面地识别和处理异常情况，从而提高数据分析的准确性和可靠性。

2.3 异常值分析方法

异常值可能对数据分析和建模产生不良影响，因此需要进行适当的处理。以下是一些常用的异常值分析方法：

（1）观察统计量：通过计算数据的基本统计量，如均值、中位数、标准差等，来识别与其他观测值明显不同的数据点。

（2）直方图和箱线图：绘制数据的直方图和箱线图，可以帮助可视化数据的分布情况，并识别离群值。

（3）散点图：绘制数据的散点图，可以发现与其他数据点明显不符的异常值。

（4）统计方法：使用统计方法，如Z-score或IQR（四分位数间距）方法，来判断数据点是否偏离正常范围。Z-score可以测量一个数据点与均值之间的差异程度，而IQR可以测量数据点与四分位数之间的差异程度。

（5）领域知识和业务经验：根据特定领域的知识和业务经验，对数据进行合理的判断和筛选，识别可能存在的异常值。

2.3 处理异常值方法

处理异常值的方法通常包括以下几种：

• 删除异常值：如果确定某个数据点是异常值且对分析结果产生负面影响，可以选择将其从数据集中删除。
• 替换异常值：将异常值替换为合理的值，可以使用均值、中位数或通过插值等方法进行替换。
• 分组处理：根据特定的业务需求，将数据分组，并对每个组别的异常值进行单独处理。
• 使用异常检测算法：使用机器学习或统计学习的异常检测算法来自动识别和处理异常值。

需要根据具体的数据和分析任务来选择合适的异常值分析方法和处理策略。同时，需要在处理异常值时保持谨慎，避免过度处理或错误地删除重要的数据点。

3. 对比分析

3.1 概述

对比分析是一种常用的数据分析方法，用于比较不同时间点、不同对象或不同组别之间的数据差异和相似性。在对比分析中，常用的指标包括绝对数和相对数。

3.2 绝对数比较与相对数比较

3.2.1 绝对数比较

绝对数比较：绝对数比较是直接比较不同对象或组别的绝对数值。它关注不同对象之间的差异或绝对水平。通过绝对数比较，可以直观地了解不同对象的具体数值差异。例如，比较两个城市的人口数量、比较不同产品的销售额等。绝对数比较不考虑数据的比例关系，只关注具体数值的大小。

3.2.2 相对数比较

相对数比较：相对数比较是通过计算和比较相对数值来揭示不同对象或组别之间的比例关系或相对差异。相对数比较可以帮助我们了解不同对象在整体中的相对地位或比例关系。

常见的相对数比较包括比率、百分比、指数、变动率等。相对数比较考虑数据的比例关系，可以更好地展示对象之间的相对差异或趋势。例如，比较两个城市的人口比例、计算某个指标在总体中的百分比、比较不同时间点的指标变化率等。

3.2.3 相对数

（1）结构相对数：结构相对数用于分析数据的组成结构或分布情况。它通过比较不同部分在整体中的比例或占比来揭示数据的结构特征。常见的结构相对数包括组成比例、部分占比等。

例如，可以使用结构相对数来比较不同产品在总销售额中的占比，或者比较不同产业在国民经济中的比重。

（2）比例相对数：比例相对数用于比较不同对象或组别之间的比例关系。它可以帮助我们了解数据的相对比例和分布情况。常见的比例相对数包括比率、百分比等。

例如，可以使用比例相对数来比较两个城市的人口比率，或者计算某个指标在总体中的百分比。

（3）比较相对数：比较相对数用于比较不同对象或组别之间的差异或相似性。它可以揭示数据之间的相对差异或趋势。常见的比较相对数包括指数、变动率等。

例如，可以使用比较相对数来比较两个时间点的指标变化趋势，或者比较不同地区的经济增长率。

（4）动态相对数：动态相对数用于分析数据的变化趋势和动态性质。它可以帮助我们了解数据在不同时间点的变化情况和趋势。常见的动态相对数包括增长率、变动率等。

例如，可以使用动态相对数来计算年度销售额的增长率，或者比较不同季度的经济变动率。

（5）强度相对数：强度相对数用于衡量某个指标的强度或强度比较。它可以帮助我们了解某个现象或指标的强度水平和相对差异。常见的强度相对数包括密度、强度比等。

例如，可以使用强度相对数来比较不同地区的人口密度，或者比较不同产品的市场份额。

3.3 比较的方面

3.3.1 时间方面的比较：

• 绝对数比较：比较不同时间点的绝对数值，例如比较两个季度的销售额或两年间的利润变化。
• 相对数比较：计算和比较不同时间点的相对数值，例如比较某指标在不同时间点的增长率或变动幅度。

3.3.2 空间方面的比较：

• 绝对数比较：比较不同地区或不同部门的绝对数值，例如比较不同城市的人口数量或不同分公司的销售额。
• 相对数比较：计算和比较不同地区或不同部门的相对数值，例如比较不同城市的人口增长率或不同分公司的市场占有率。

3.3.3 经验与计划的比较：

• 绝对数比较：比较实际结果与预期计划之间的差异，例如比较实际销售额与预期销售额的差距或实际成本与预算成本的差异。
• 相对数比较：计算和比较实际结果与预期计划之间的相对数值，例如比较实际销售额与预期销售额的增长率或实际成本与预算成本的偏差率。

4. 结构分析

4.1 概述

结构分析是一种用于理解和描述数据的组成和关系的方法。它可以从静态和动态的角度进行分析，同时可以关注整体和部分的结构。

4.2 静态与动态

（1）静态结构分析： 静态结构分析关注数据的当前状态或瞬时状态，主要包括以下两个方面：

• 总体结构分析：对整体数据进行分析，了解其组成部分之间的比例、比例关系和分布情况。例如，可以分析一个国家的人口结构，了解不同年龄组的人口比例和比例关系。
• 部分结构分析：对特定部分或子群体的数据进行分析，了解其内部的组成和特点。例如，可以分析某个城市的行业结构，了解不同行业的就业人数和比例。

（2）动态结构分析： 动态结构分析关注数据的变化和演变过程，主要包括以下两个方面：

• 动态比较分析：比较不同时期的数据，了解其变化趋势和幅度。例如，可以比较不同年份的销售额，分析销售额的增长或下降情况。
• 动态关系分析：分析数据之间的相互关系和相互作用，了解其变化规律和影响因素。例如，可以分析不同变量之间的相关性，了解它们之间的动态关系。

结构分析可以通过各种统计方法和可视化工具来实现，例如表格、图表、图形等。它有助于揭示数据的内在结构、特点和趋势，为决策提供基础和指导。

5. 分布分析

5.1 概述

分布分析是指对数据的分布特征进行统计和分析的过程，目的是了解数据的概率分布及其性质。在分布分析中，可以使用多种方法来获得概率分布，并判断是否符合正态分布。

5.2 判断方法

5.2.1 直接获得概率分布

直接获得概率分布：对于某些数据，如果已经知道其概率分布类型（如正态分布、泊松分布等），则可以直接根据概率分布函数获得相应的概率分布。例如，对于正态分布，可以使用正态分布的概率密度函数来获得其分布。

5.2.2 极大似然估计

极大似然估计：对于一组观测数据，可以通过极大似然估计方法来估计其概率分布的参数。极大似然估计是一种通过最大化观测数据出现的可能性来确定参数值的方法。通过估计参数，可以得到符合观测数据分布的概率分布函数。

（1）正态分布的极大似然估计：

• 对于已知数据服从正态分布的情况，可以使用极大似然估计来估计正态分布的参数，即均值和方差。
• 极大似然估计的目标是找到最大化样本观测值出现概率的均值和方差，使得观测数据的出现概率最大。
• 常用的方法是通过计算样本的均值和方差来估计正态分布的参数。

（12）t分布的极大似然估计：

• t分布是用于小样本情况下的概率分布，适用于样本容量较小或总体方差未知的情况。
• 在极大似然估计中，可以使用t分布的似然函数来估计t分布的参数，即自由度。
• 通过最大化样本观测值在t分布下出现的可能性来估计t分布的自由度。

（3）F分布的极大似然估计：

• F分布是用于比较两个样本方差是否显著不同的概率分布。
• 极大似然估计可应用于F分布的参数估计，即分子自由度和分母自由度。
• 通过最大化样本观测值在F分布下的概率来估计F分布的自由度。

5.2.3 正态性检验

正态性检验：为了判断数据是否服从正态分布，可以使用各种统计方法进行正态性检验。常见的正态性检验方法包括Kolmogorov-Smirnov检验、Shapiro-Wilk检验和Anderson-Darling检验等。这些检验方法基于观测数据与正态分布的拟合程度来判断数据是否符合正态分布。