1、隐马尔可夫模型HMM

1.1Sequence2Sequence

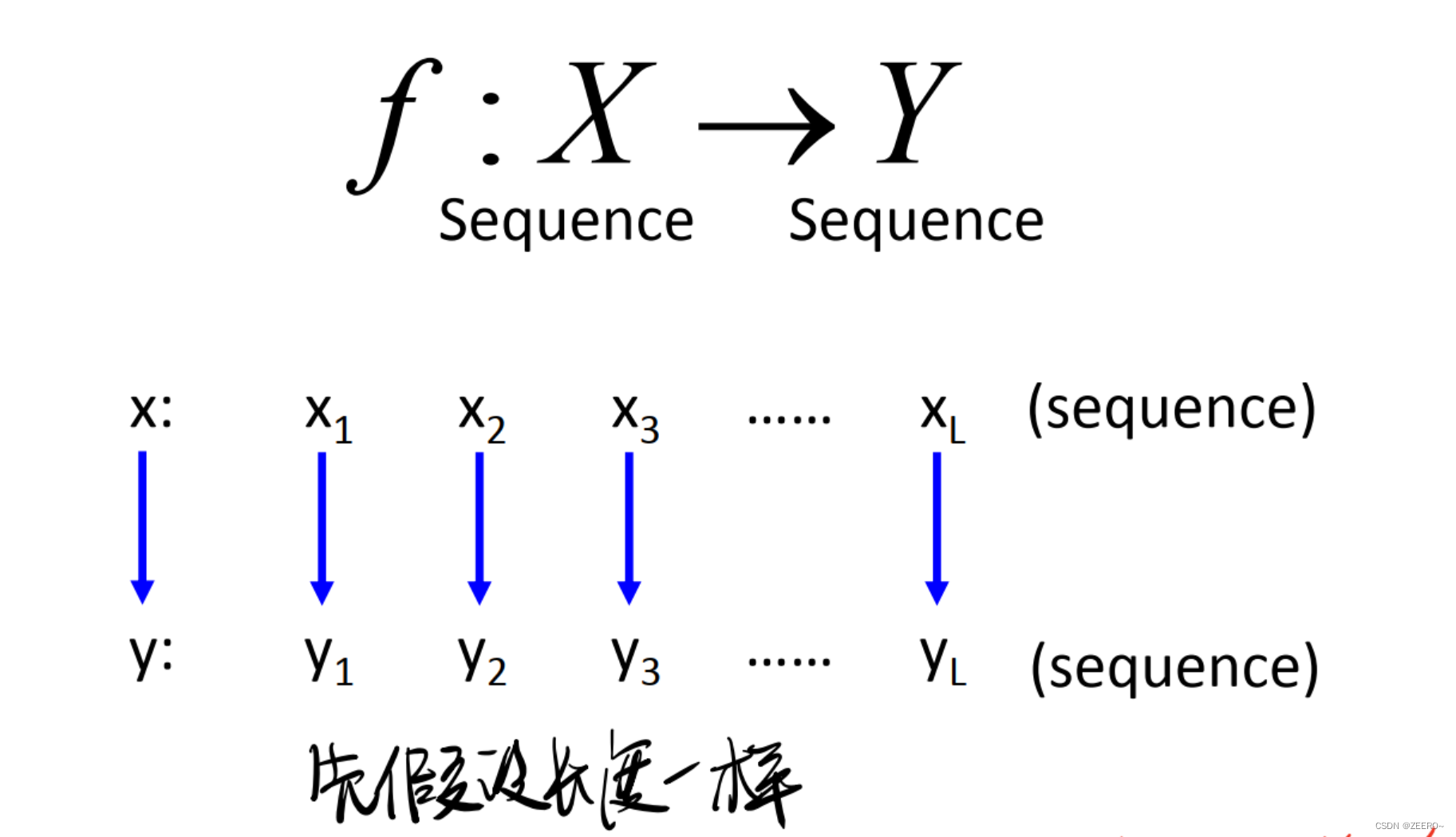
什么是Seq2Seq问题呢？简单来说，就是输入是一个序列，输出也是一个序列。输入和输出的序列可以相等，也可以不相等。在本文中，可以先假设输入输出序列相等。
在这里插入图片描述

1.2 HMM

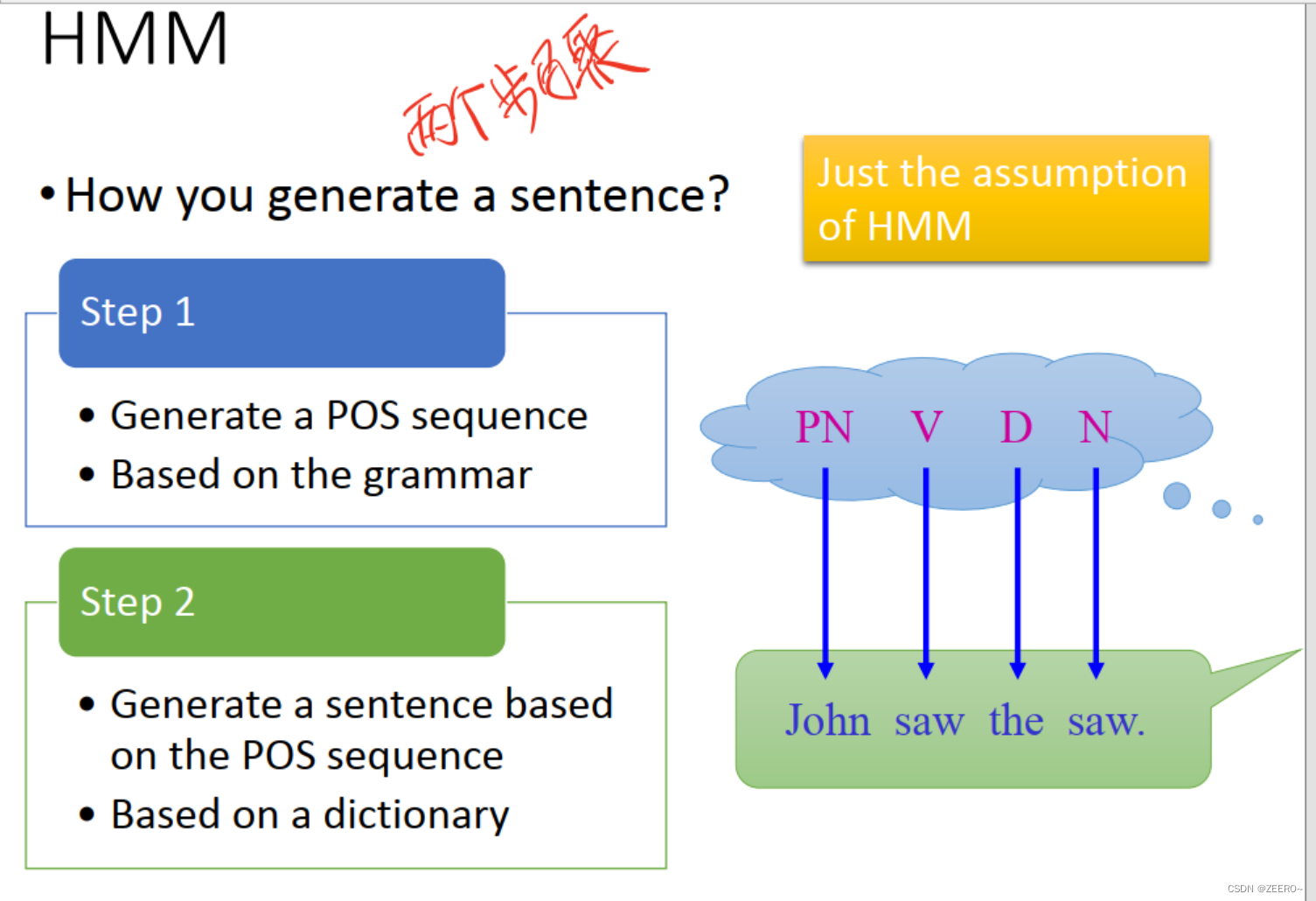
这里用了一个通俗易懂的例子来解释HMM模型，POS tagging，词性标注。
在这里插入图片描述
PN表示专有名词Proper Noun
V表示动词
D 定冠词
N名词

通常情况下，我们要生成1个句子，可以分为2个步骤。
一、根据语法设计好一个词性序列
二、根据字典中的词汇填充生成一个句子。
在这里插入图片描述
举例子来说，

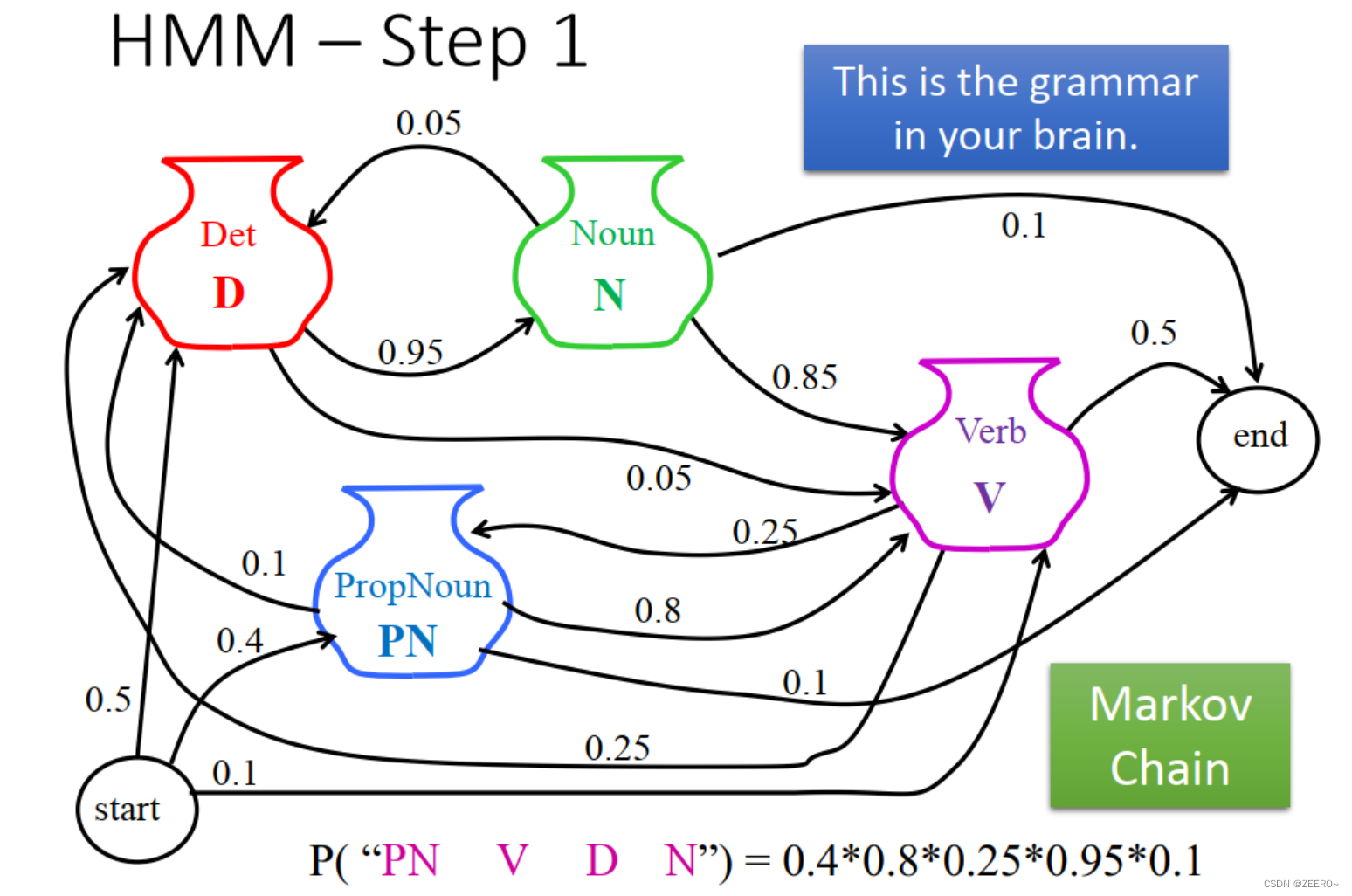
图片表示，开始start后面接的词为PN的概率是0.4，接动词V的概率是0.1，接定冠词D的概率是0.5。依次类推。这样，第一步构思的词性顺序为 PN V D N的概率则为0.40.80.250.950.1。

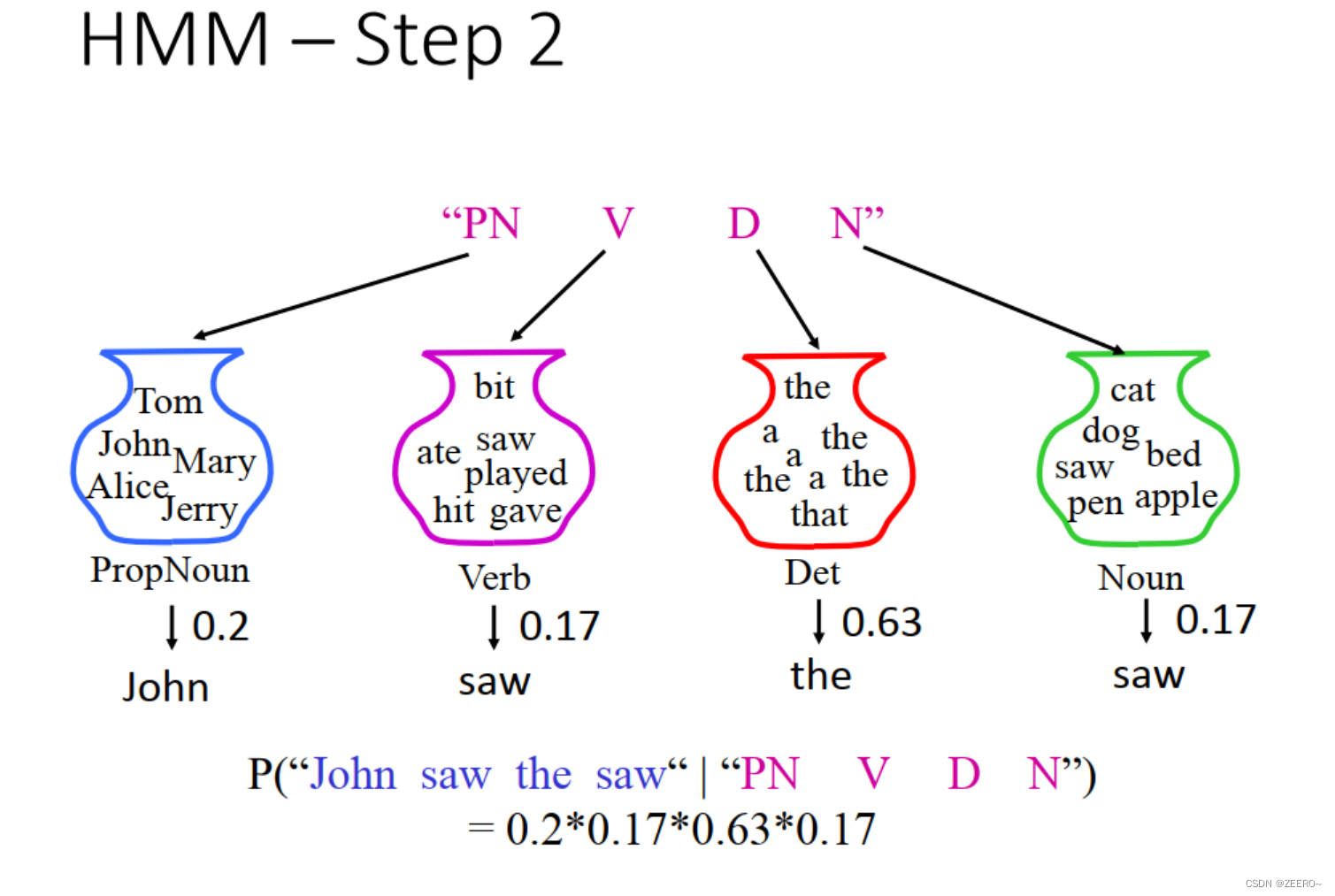
类似地，在词性结构已经是PN V D N的第一步的基础上，生成的句子为 John saw the saw的概率为0.20.170.63*0.17。

那怎么计算第2步的概率呢？
在这里插入图片描述

计算方法如上图所示，其中y表示词性，x表示单词。我们是根据词汇x来求目标词性y，目标词性y是隐含的变量，这也是HMM中隐的由来。
现在问题只在于说如何计算。其实很简单，可以直接根据训练数据将这些概率统计出来。
在这里插入图片描述

如上图所示，词性 $s^{'}$ 接在词性 $s$ 后面的概率为训练数据中词性s后面出现词性 $s^{'}$ 的次数除以词性s出现的总次数。
词性s的单词为特定单词t的概率则为训练数据中所有单词为t且词性属于s的次数除以词性s出现的总次数。
在这里插入图片描述
通过对训练数据中的相关词汇和词性进行统计，便可计算出相应的概率。

1.3 Viterbi算法

在这里插入图片描述
上述可知，假设有 $∣ S ∣$ 个词性，序列长度为L。那么该序列的词性可能存在 $S|^{L}$ 种答案。计算复杂度很高。而Vertibi算法则是专门解决该问题而衍生出的优化算法。

概括来说，HMM可分为上述3个步骤。

1.3 HMM模型的缺点

在这里插入图片描述
举个例子来说，假如训练数据中， $y_{l-1}$ 为名词N，后面接动词V的概率为0.9，接定冠词D的概率为0.1。而在给定词性为动词V的条件下，该单词为单词a的概率为0.5，为单词c的概率为0.5。在给定词性为D的条件下，为单词a的概率为1。
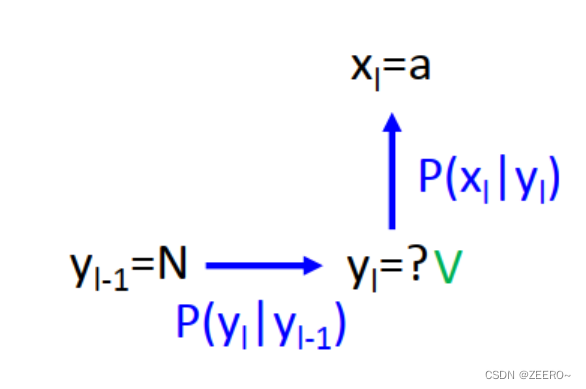
在这里插入图片描述
现在我们假设出现了该种场景，第一个单词为N，后一个单词为a，求后一个单词的词性预测。
这个例子比较简单，可以直接穷举出来。假如该单词词性 $y_{l}=D$ ，那么概率p=0.11=0.1。
假如该单词词性 $y_{l}=V$ ,p=0.90.5=0.45。因此，答案应该为V。
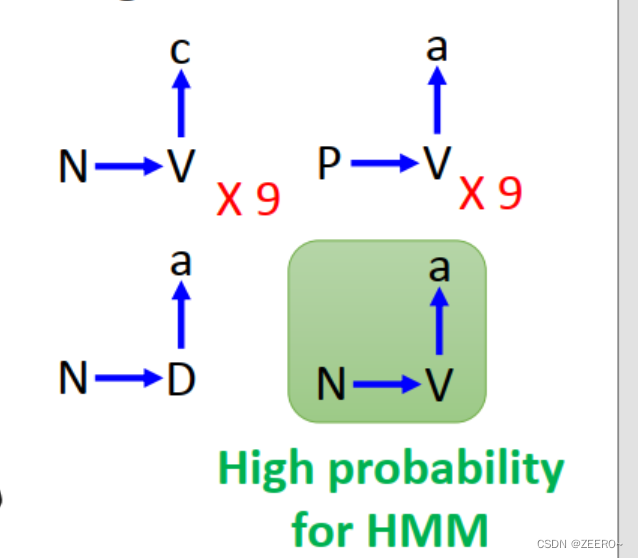
在这里插入图片描述
这个答案V看上去是没有问题的，但是假设我们的训练数据是上述这种情况，完全满足Transition probability 和Emission probability情况。我们预测的最佳答案是N-V-a。
但是，我们的训练数据中原本就出现了N-D-a这种样本。HMM模型所给的答案是训练数据中从未见过的情况，因为其概率最大。这种情况我们认为HMM预测的更好还是原数据更好呢？
答案显然是原数据中出现的样本最好。由此引申出HMM模型的缺陷问题：可能会预测出训练数据中从未出现过的结果。在训练数据为小样本数据集时其实时有一定好处的，因为这样泛化能力更强。
要想解决HMM的缺陷，有2种解决思路，一是使用更为复杂的模型，而是使用条件随机场CRF。