文章目录
- 一、背景
- 二、方法
- 三、效果
论文:Exploring Simple Siamese Representation Learning
出处:FAIR | 何恺明大佬
本文作者抛出了两个爆炸💥性结论:
-
结论一:基于孪生网络的对比的学习的成功,不源于 predictor、BN、l2-norm,而是源于一个分支梯度截断(但作者最终也没有给出一个很好的解释,只是证明了这个结论)
-
结论二:孪生网络其实是在学习输入不变性,也就是对同一输入经过不同的数据增强,输出保持不变的能力(类似于 CNN 中的平移不变性,但孪生网络学习的不变性更复杂更难)
一、背景
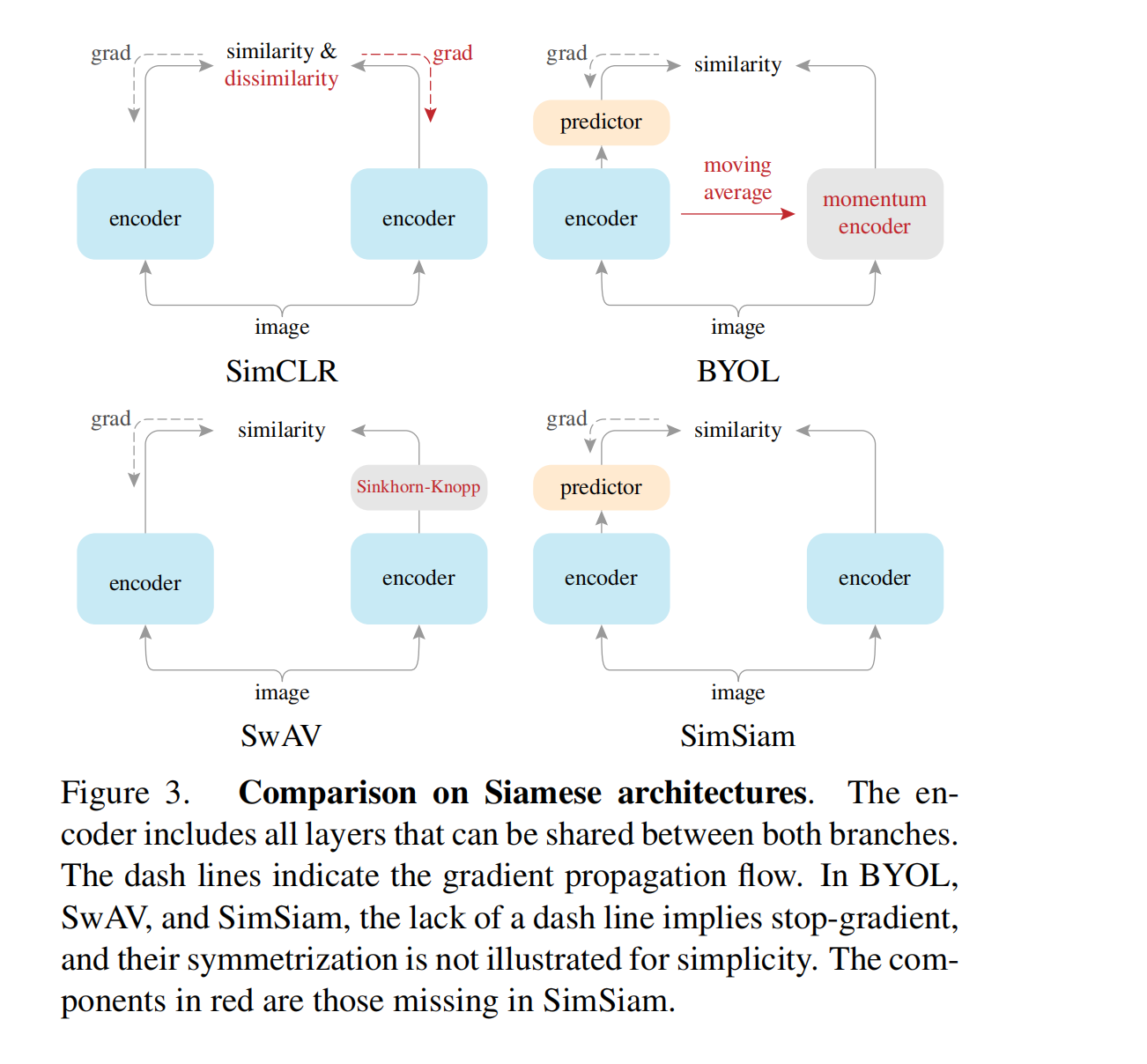
无监督学习算是被孪生网络玩明白了,典型的方法如 MOCO、SimCLR、BYOL 等都是孪生网络的结构,其训练模型的主要目的就是最大化来自同一图片的两个 augmentation views 的相似度。
但是,孪生网络有一个最大的问题就是模态坍塌,也就是所以输出都坍塌成一个常数,这样 loss 永远为零,模型找到了一个捷径,不用学习。
为了在使用孪生网络的同时避免模型坍塌,很多方法提出了一些限制条件:
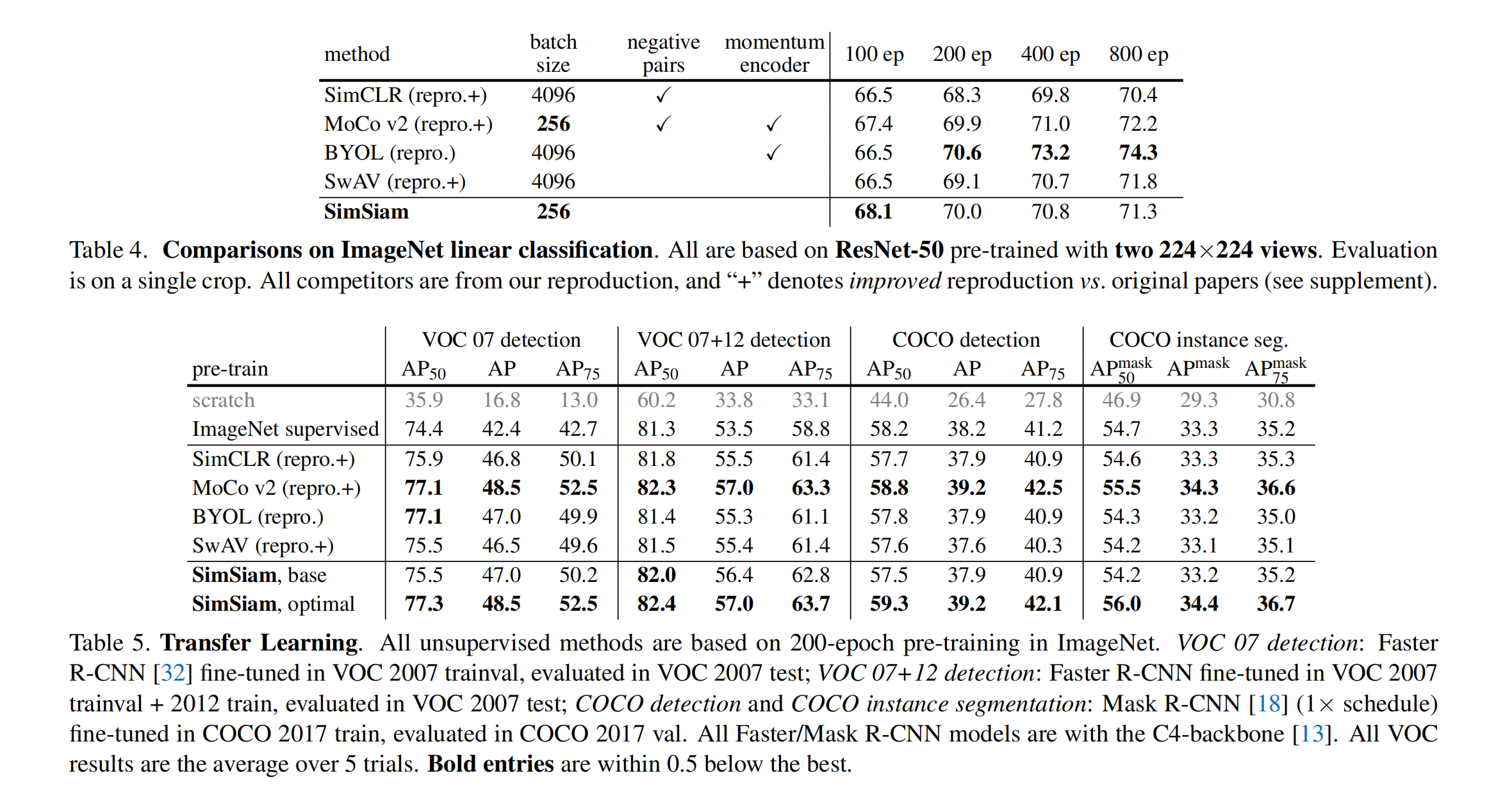
- SimCLR 中使用超大的 batch size (4096)引入负样本来提升对比学习的难度
- SwAV 引入了在线聚合方式
- BYOL 舍弃了负样本,使用了不对称的孪生网络结构和 momentum encoder 的方式,也避免了模型坍塌
SimSiam 的特点:
-
SimSiam 作者证明在不使用负样本、large batch、momentum encoder 的情况下,孪生网络也能学习的很好,而且通过实验证明了这个结论
-
SimSiam 作者证明避免模型坍塌最重要的一点是使用梯度截断,而不在于对 loss 或模型结构的限制
SimSiam 的结构可以看做:
- “BYOL without the momentum encoder”
- “SimCLR without negative pairs”
- “SimCLR without negative pairs”
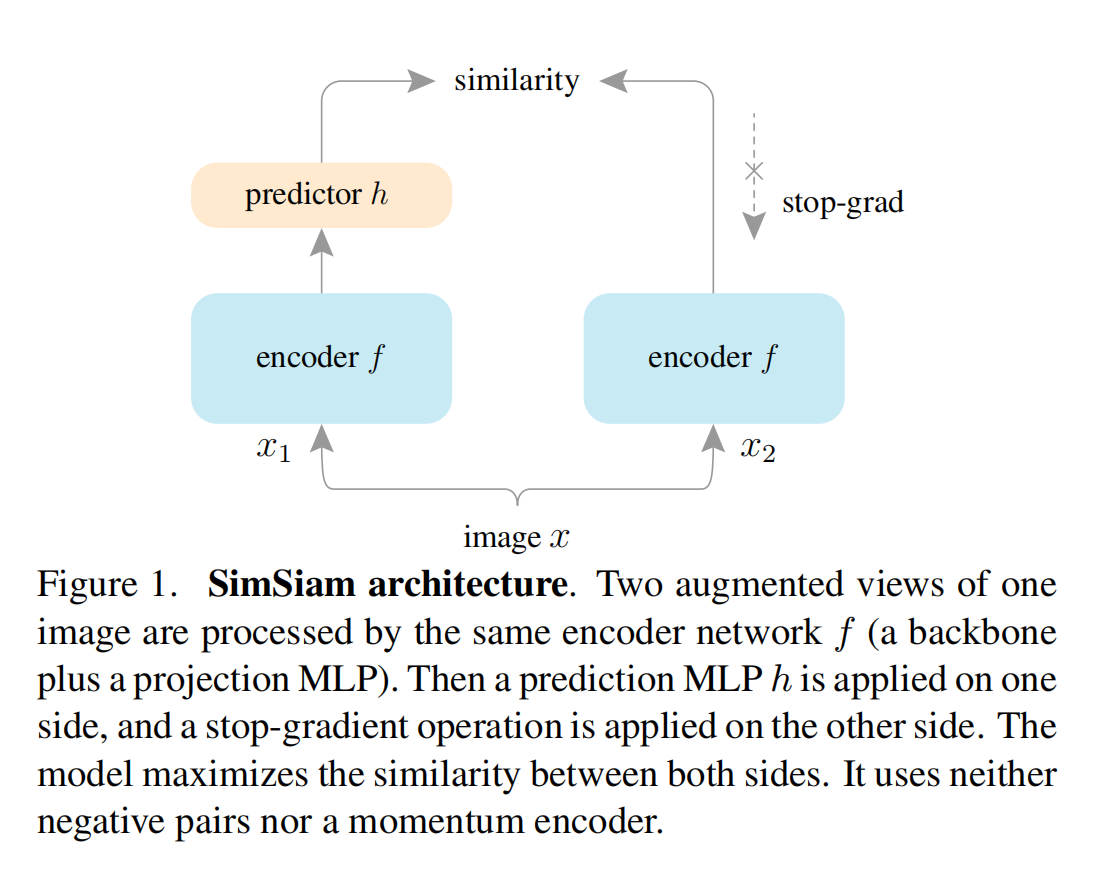
图 1 展示了 SimSiam 的结构,又一次证明了打败恺明大佬的只有他自己,完全拿掉了 MOCO 他亲自提出的 momentum encoder 和 queue 的模块,两个蓝色的 encoder 模块参数完全相同,左边多了一个 predictor,这个 predictor 是经过前面几个大佬的方法(SimCLR、BYOL等)证明的一个非常有用的模块,右边不进行梯度回传,直接使用左边的参数来更新自己即可。
看到这里我们不禁怀疑了,为什么之前各种的负样本、大 batch、momentum encoder 在这里都舍弃了,模型却还能很好的工作
作者在这里提出一个新的观点(但没有得到很好的证明):
-
梯度截断的方法既然有效,那就说明梯度截断问题是一个新的未被解决的隐藏的问题
-
作者假设这里隐藏了两组变量,而且 SimSiam 的行为看起来是在这两组参数中进行有选择的优化
孪生网络的隐藏任务:学习不变性(一个图像经过复杂数据增强后,输出不变)
-
作者用简单的 baseline 表明,孪生网络这个结构是对比对比学习成功的关键所在,其原因在于孪生网络可以为模型不变性引入归纳偏置,这里的不变性就是说同一输入的两个不同视角经过处理后应该有相同的输出
-
哎呀这不和 CNN 中的归纳偏置联系起来了吗,这不很像 CNN 中的平移不变性嘛
-
所以,参数共享的孪生网络能够根据更复杂的变化(平移、缩放、随机抠图等)构建模型的不变性
看到这里,悟了!佩服大佬的总结升华能力!膜拜!
二、方法
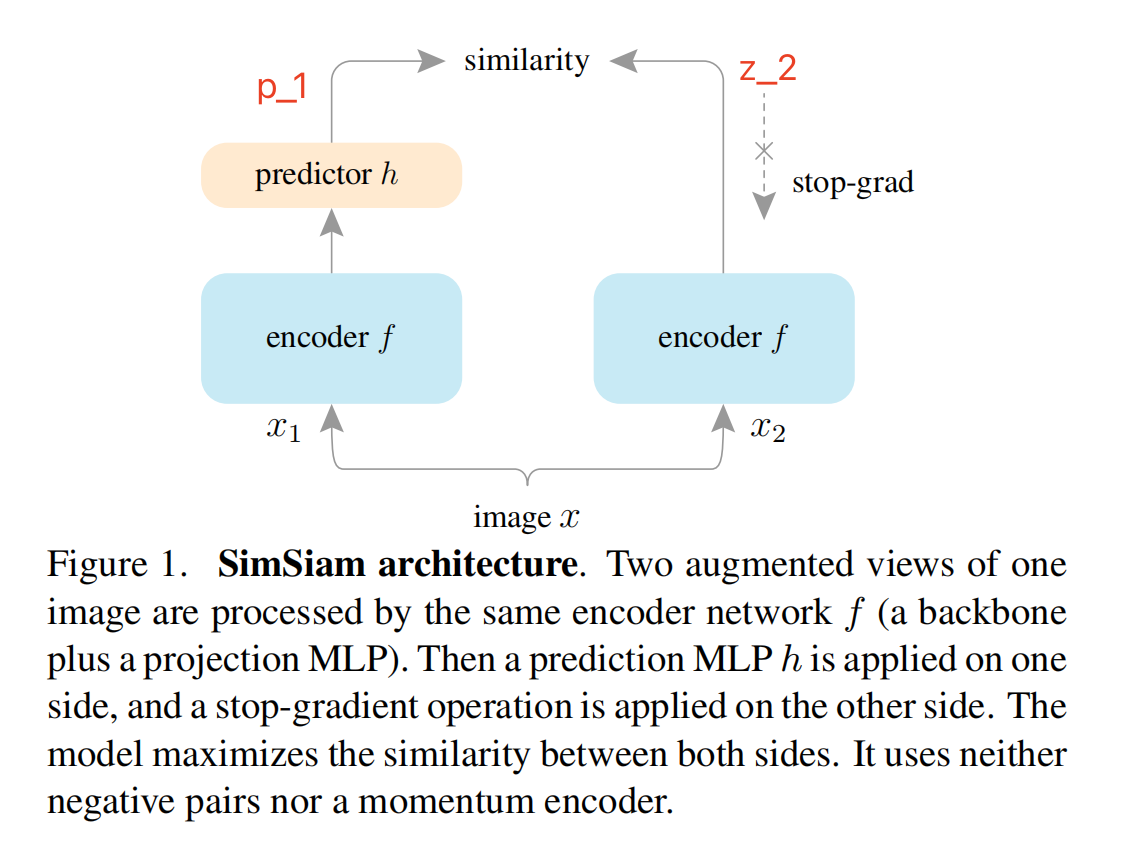
SimSiam 的总体结构如图 1 所示:
-
将输入图片经过随机数据增强得到两个视角的图片 x1 和 x2
-
这两个视角的图片都经过 encoder network f f f( 由 backbone + projection MLP head 组成),两个分支的 f f f 的参数是共享的
-
在左边分支上, f f f 后面还加了一个 prediction MLP head h h h,用于将一个视角的输出进行再次转换
-
将两个分支的结果进行相似度计算,最小化 negative cosine similarity
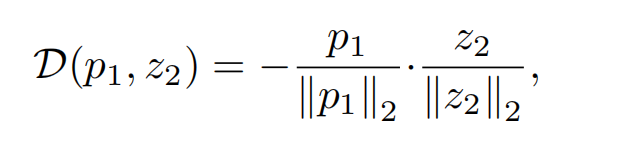
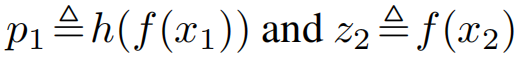
-
最后,计算对称 loss,这里 loss 的最小值为 -1,因为 cos 0=1。这里计算对称 loss 的原因是两个视角的图都会分别经过左边的分支和右边的分支,上图 1 中标红的第一种情况,就是 x1 经过左边得到 p1,x2 经过右边的分支得到 z2。还有一种情况就是 x1 经过右边的分支得到 z1,x2 经过左边的分支得到 p2。
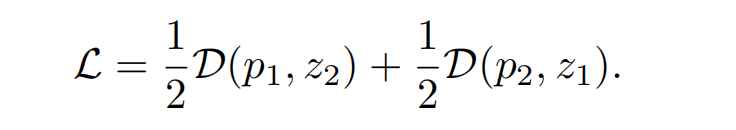
梯度截断到底起到了什么作用:为网络提供了可选择的优化路径(但没得到很好的证明)
我们知道本文最重要的一点就在于右边分支进行了梯度截断,也就是 loss 计算的时候计算的如下内容:

这就说明 z 2 z_2 z2 一直被当做常数,所以上面的 L 公式在本文的前提下被重写如下:
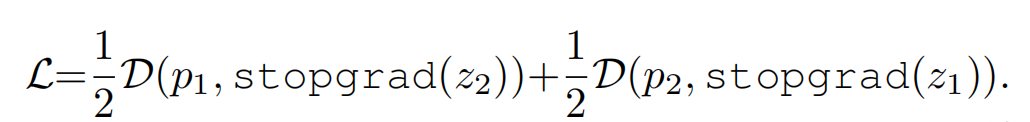
所以,梯度截断的效果在于:
- x 2 x_2 x2 的 encoder 不会从 z 2 z_2 z2 获得任何梯度,但能从 p 2 p_2 p2 中获得梯度( p 2 p_2 p2 就是 x 2 x_2 x2 输入 f f f 后得到的输出)
- x 1 x_1 x1 的 encoder 不会从 z 1 z_1 z1 获得任何梯度,但能从 p 1 p_1 p1 中获得梯度( p 1 p_1 p1 就是 x 1 x_1 x1 输入 f f f 后得到的输出)
图 2 展示了梯度截断对模型的影响:
- 如最左侧所示,没有梯度截断时(橘色),模型能很快的找到一个捷径解, loss 被优化为 -1
- 为了探索这种捷径解是不是源于模型坍塌,作者对输出求了标准差,如果输出坍塌为了一个常数,则所有通道的总体的标准差就会变为 0,如中间图橘色所示
- 如果模型正常迭代,输出是一个均值为 0 的高斯分布,那么标准差就是 1 / d 1/\sqrt d 1/d,如中间图蓝色所示,也就是有梯度截断的时候,输出是正常的
- 如最右侧所示,展示了 KNN 分类器的验证集的效果,有梯度截断的时候,KNN 分类器的效果是逐步上升的
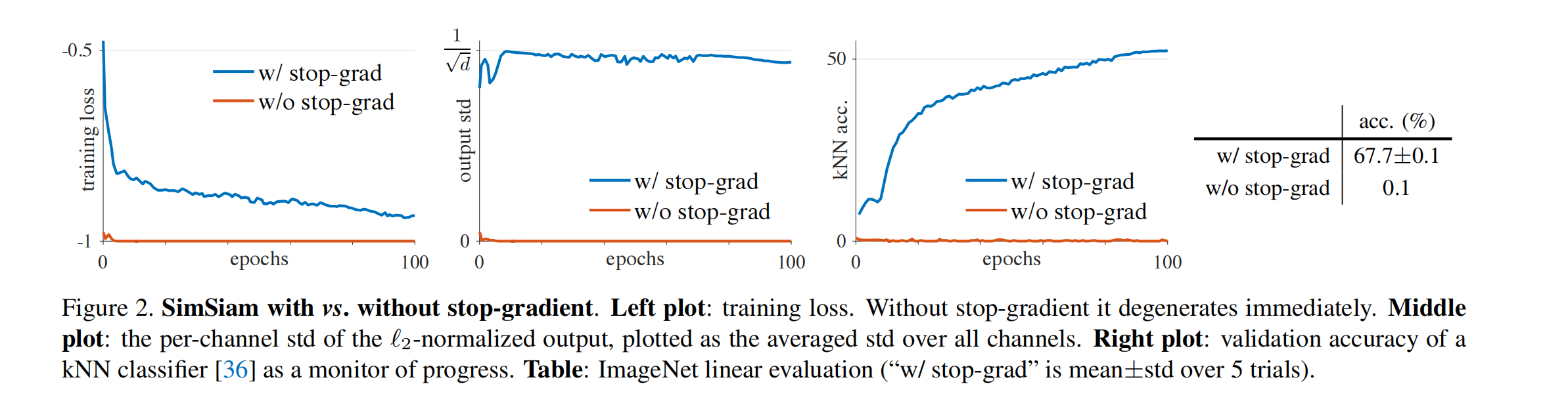
作者用这个实验证明了,尽管有 BN、predictor、l2-norm,模型也会坍塌,因为在模型的设置中唯一改变的就是是否进行了模型梯度截断。
为了证明这个结果,作者进行了一系列的推断,但还是没有一个很好的结论
最后作者给出了自己的一个理解:
- 孪生网络是交替优化的,就是两个样本会分别送入左边分支和右边分支,而只有左边的分支是进行梯度更新的,所以,这种选择交替的优化模型提供了一个不同的优化轨迹,而且这个轨迹很大程度上依赖于初始化的好坏
- 如果随机初始化一个网络,那么输出可能就是常数,从这种参数上来开始优化的话, 那么所有输入对应的输出都有可能是常数
三、效果