获取凸包,可以参考我的这篇文章: 凸包(Convex Hull)代码实现案例
获取了凸包之后,可以干什么呢?
凸缺陷凸包与轮廓之间的部分称为凸缺陷。凸缺陷可用来处理手势识别等问题。
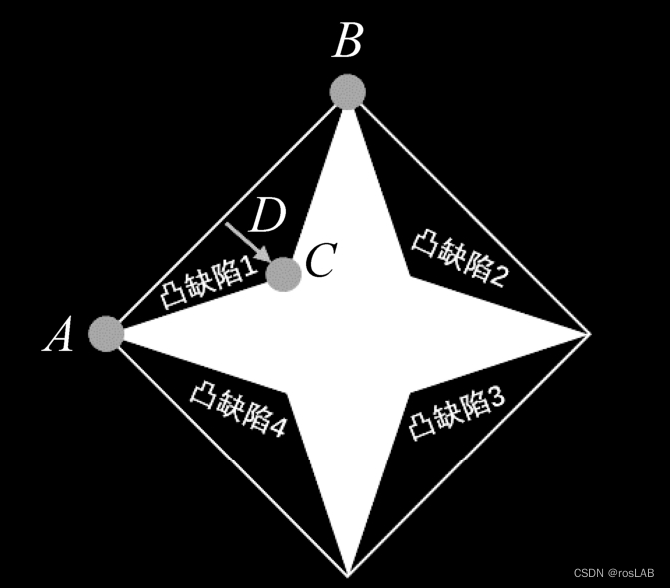
通常情况下,使用如下四个特征值来表示凸缺陷:
● 起点:该特征值用于说明当前凸缺陷的起点位置。需要注意的是,起点值用轮廓索引表示。也就是说,起点一定是轮廓中的一个点,并且用其在轮廓中的序号来表示。例如,点A是凸缺陷1的起点。
● 终点:该特征值用于说明当前凸缺陷的终点位置。该值也是使用轮廓索引表示的。例如,图8-4中的点B是凸缺陷1的终点。
● 轮廓上距离凸包最远的点。例如,点C是凸缺陷1中的轮廓上距离凸包最远的点。
● 最远点到凸包的近似距离。例如,距离D是凸缺陷1中的最远点到凸包的近似距离。
OpenCV提供了函数cconvexityDefects()用来获取凸缺陷,其语法格式如下:
CONVEXITYDEFECTS()是OpenCV库中的一个函数,主要用于计算图像中凸缺陷的信息。它可以通过输入的轮廓点信息计算出凸缺陷的数量、位置和深度等信息,可以用于手势识别、目标检测等应用场景。在C++中使用该函数时,需要包含OpenCV头文件,并按照函数参数要求输入轮廓点信息和凸包点信息等参数,然后通过输出参数获取凸缺陷信息。
void cv::convexityDefects( InputArray contour, InputArray convexhull, OutputArray convexityDefects);
函数参数说明如下:
- contour:输入的轮廓点信息,可以通过cv::findContours()函数获取。
- convexhull:输入的凸包点信息,可以通过cv::convexHull()函数获取。
- convexityDefects:输出的凸缺陷信息,是一个N行4列的矩阵,每行包含4个元素,分别是凸缺陷起点索引、终点索引、最远点索引和距离
使用CONVEXITYDEFECTS()函数的步骤如下:
-
- 读取图像并转换为灰度图像。
Mat src = imread("image.jpg");
Mat gray;
cvtColor(src, gray, CV_BGR2GRAY);
-
- 对灰度图像进行二值化处理。
Mat binary;threshold(gray, binary, 100, 255, THRESH_BINARY);
- 3.获取图像中的轮廓信息。
vector<vector<Point>> contours;
findContours(binary, contours, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE);
- 4.对每个轮廓计算凸包点信息。
vector<vector<int>> hull(contours.size());
for (int i = 0; i < contours.size(); i++){ convexHull(contours[i], hull[i], false);}
- 5.对每个轮廓计算凸缺陷信息。
vector<vector<Vec4i>> defects(contours.size());for (int i = 0; i < contours.size(); i++) { if (hull[i].size() > 3) { convexityDefects(contours[i], hull[i], defects[i]); }}
- 6.遍历所有轮廓的凸缺陷信息,并绘制凸缺陷。
for (int i = 0; i < contours.size(); i++) { for (int j = 0; j < defects[i].size(); j++) { Vec4i& v = defects[i][j]; float depth = v[3] / 256.0; if (depth > 10) { int startidx = v[0]; Point start(contours[i][startidx]); int endidx = v[1]; Point end(contours[i][endidx]); int faridx = v[2]; Point far(contours[i][faridx]); line(src, start, end, Scalar(0, 0, 255), 2); line(src, start, far, Scalar(0, 255, 0), 2); line(src, end, far, Scalar(0, 255, 0), 2); circle(src, far, 4, Scalar(0, 255, 0), -1); } }
}
这样就可以计算图像中轮廓的凸缺陷信息,并绘制凸缺陷。
总结一下,CONVEXITYDEFECTS()函数是OpenCV中用于计算轮廓凸缺陷信息的函数,可以用于手势识别、目标检测等应用场景。使用该函数时,需要先获取轮廓和凸包信息,然后使用该函数计算凸缺陷信息,并根据需求对凸缺陷进行处理和绘制。
应用:
针对手势进行凸缺陷检测,可以实现手势识别。此时,仅计算指缝间的凸缺陷个数,根据该值识别手势表示的数值。
例如
● 有4个凸缺陷时,手势表示数值5。
● 有3个凸缺陷时,手势表示数值4。
● 有2个凸缺陷时,手势表示数值3。
● 有1个凸缺陷时,手势表示数值2。
● 有0个凸缺陷时,手势可能表示数值1,也可能表示数值0。