一个服务器多实例复制完成
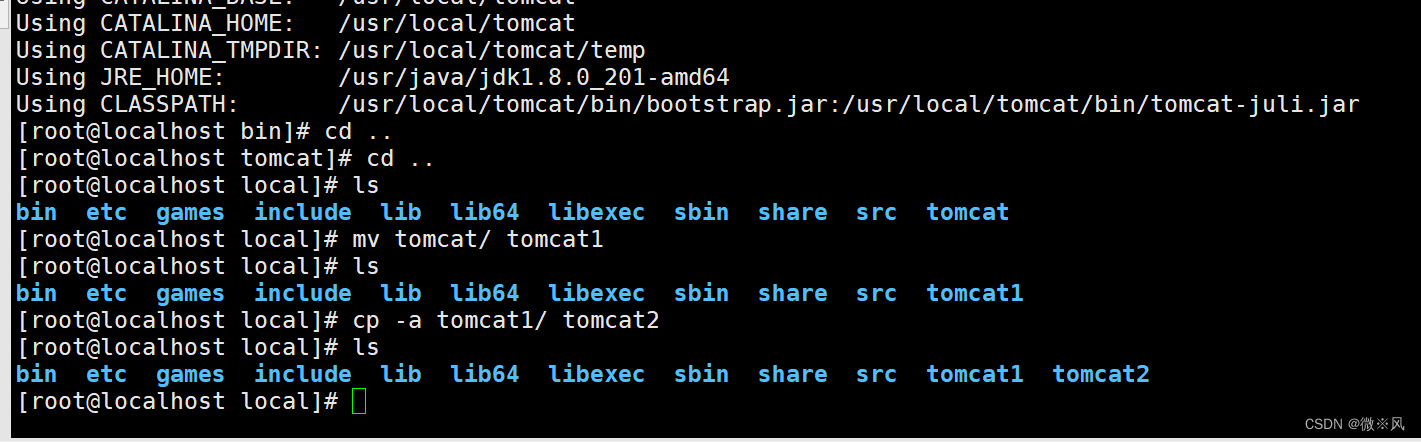
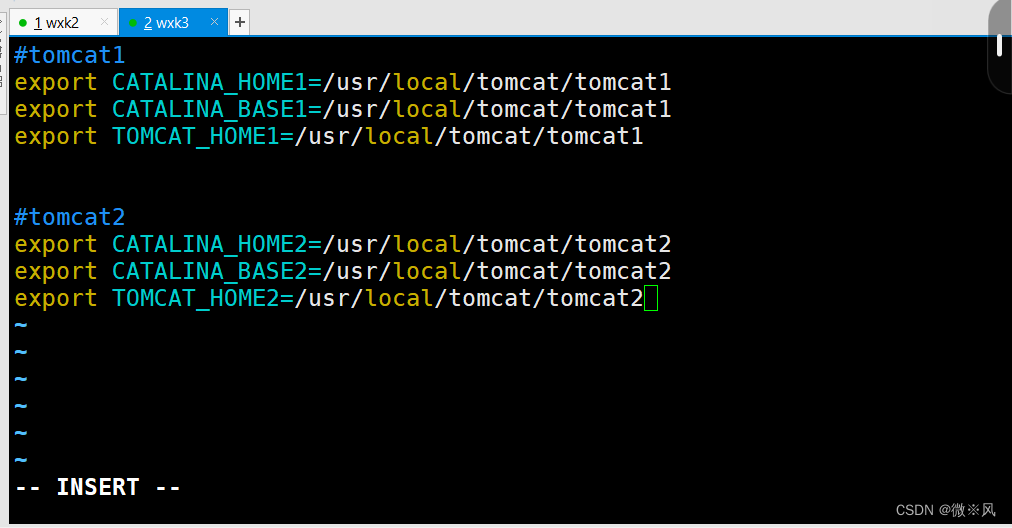
配置tomcat多实例的环境变量
vim /etc/profile.d/tomcat.sh配置tomcat1和tomcat2的环境变量
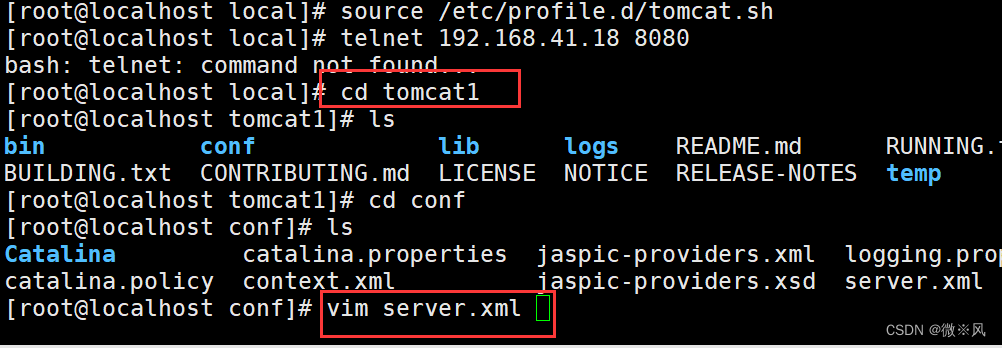
进入tomcat1修改配置
测试通信端口是否正常
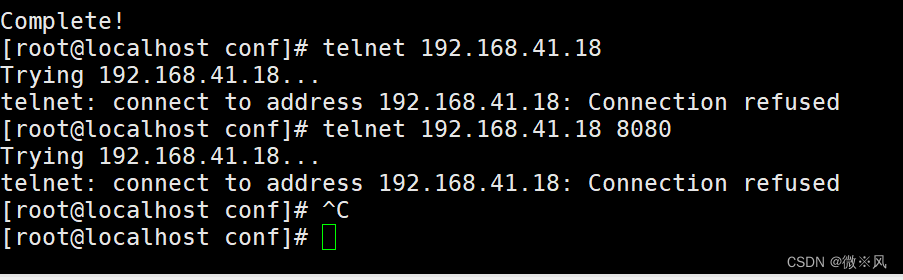
连接正常
toncat 2 配置修改
修改这三个



端口配置修改完成
修改tomcat1
shudown
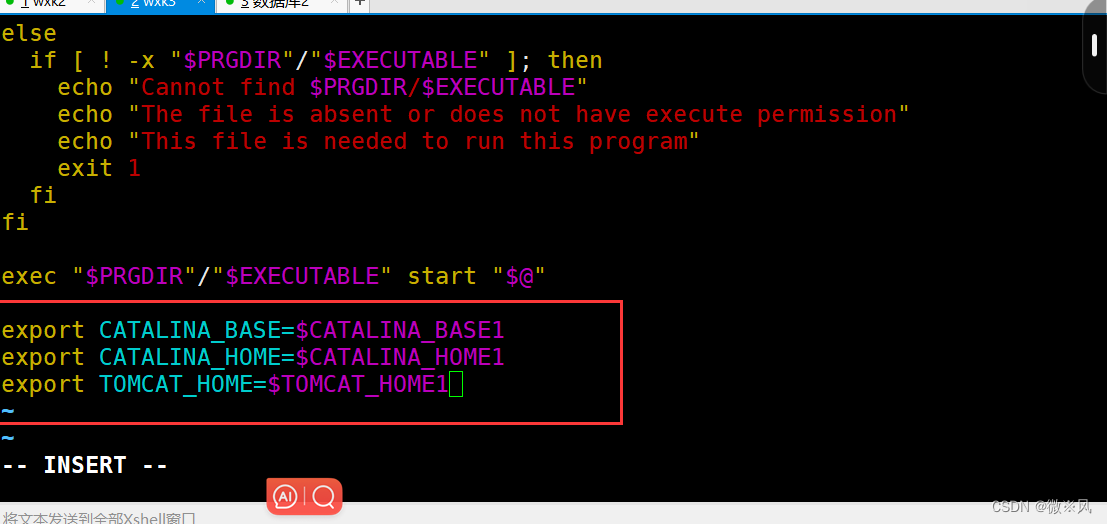
分别把启动文件指向tomcat1
tomcat2
修改tomcat2
添加文件同理
tomcat1 2 多实例配置完成
开启tomcat2服务

开启tomcat1服务
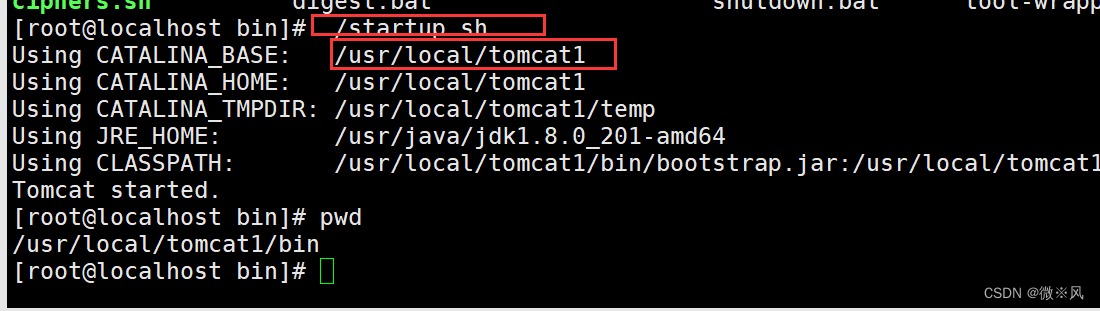
tomcat2 成功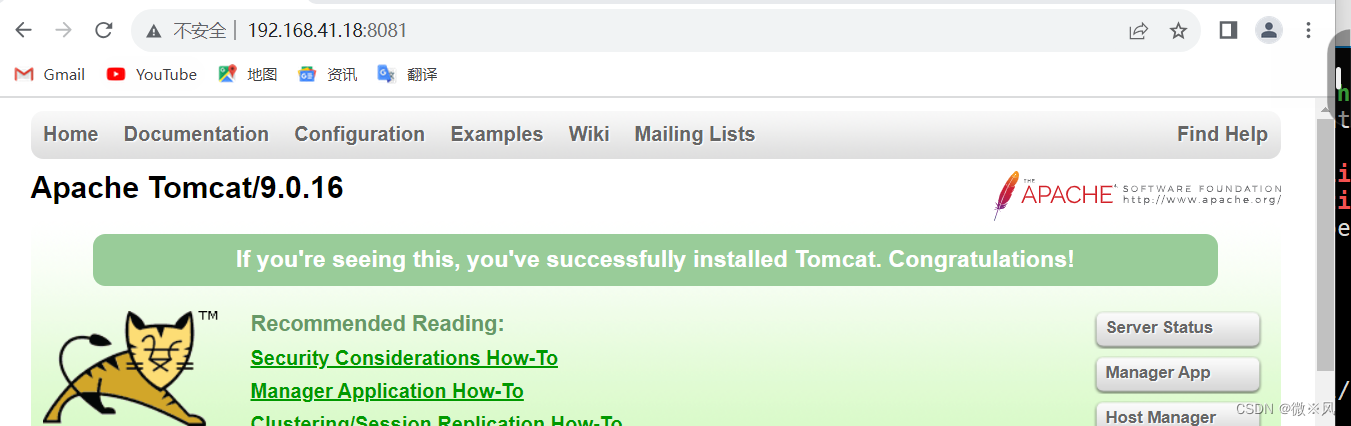
tomcat1成功
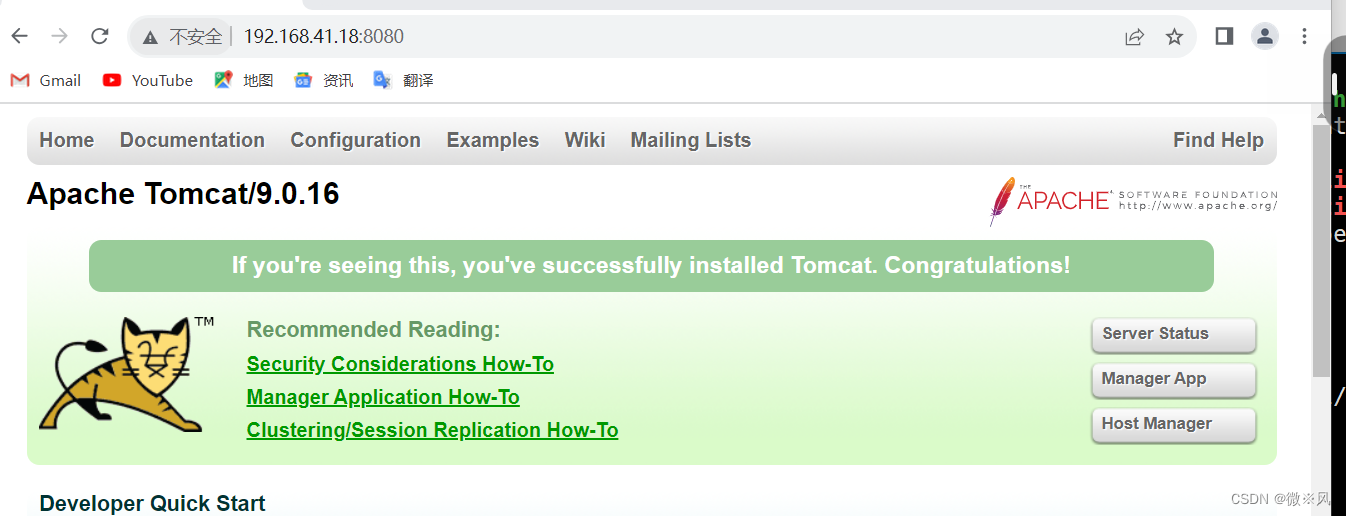
nginx和tomcat实现动静分离
nginx配置
设置调用地址并配置权重

动态请求配置
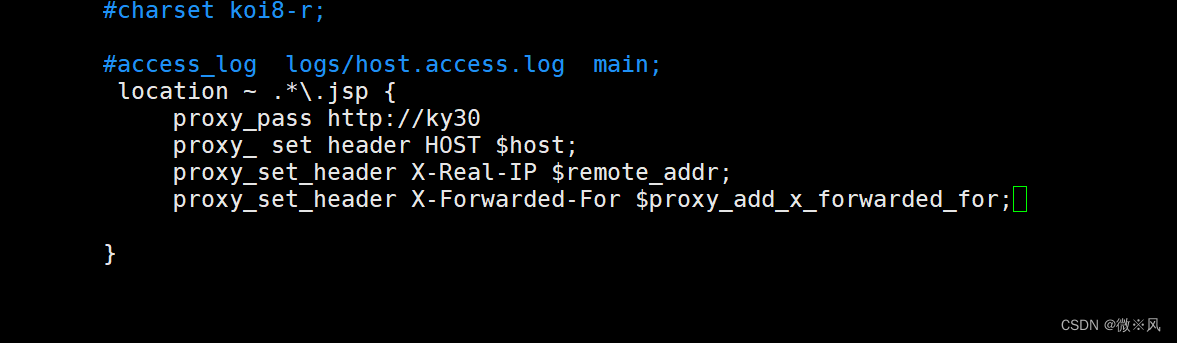
proxy_pass http://tomcat_server;
#设置后端的Web服务器可以获取远程客户端的真实IP
proxy_set_header HOST $host;
#把$remote_addr赋值给X-Real-IP,来获取源IP
proxy_set_header X-Real-IP $remote_addr;
#在nginx 作为代理服务器时,设置的IP列表,会把经过的机器ip,代理机器ip都记录下来
proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
}
#配置Nginx处理静态图片请求
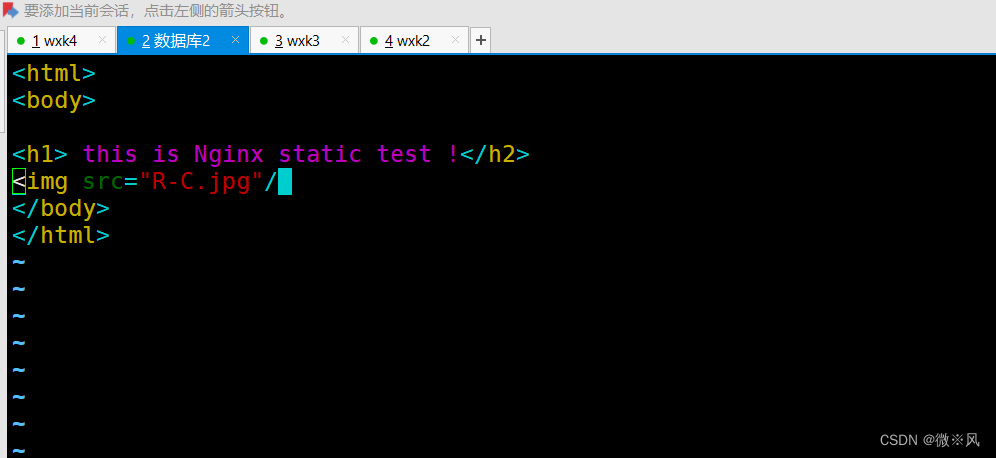
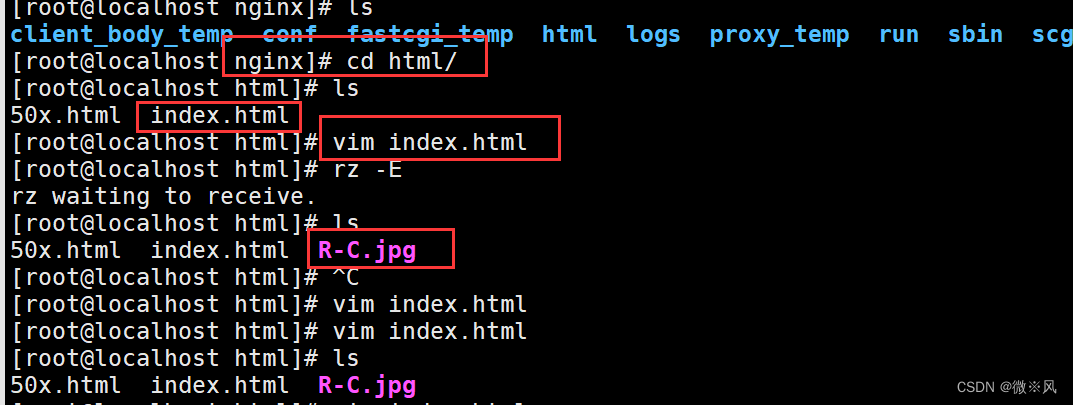
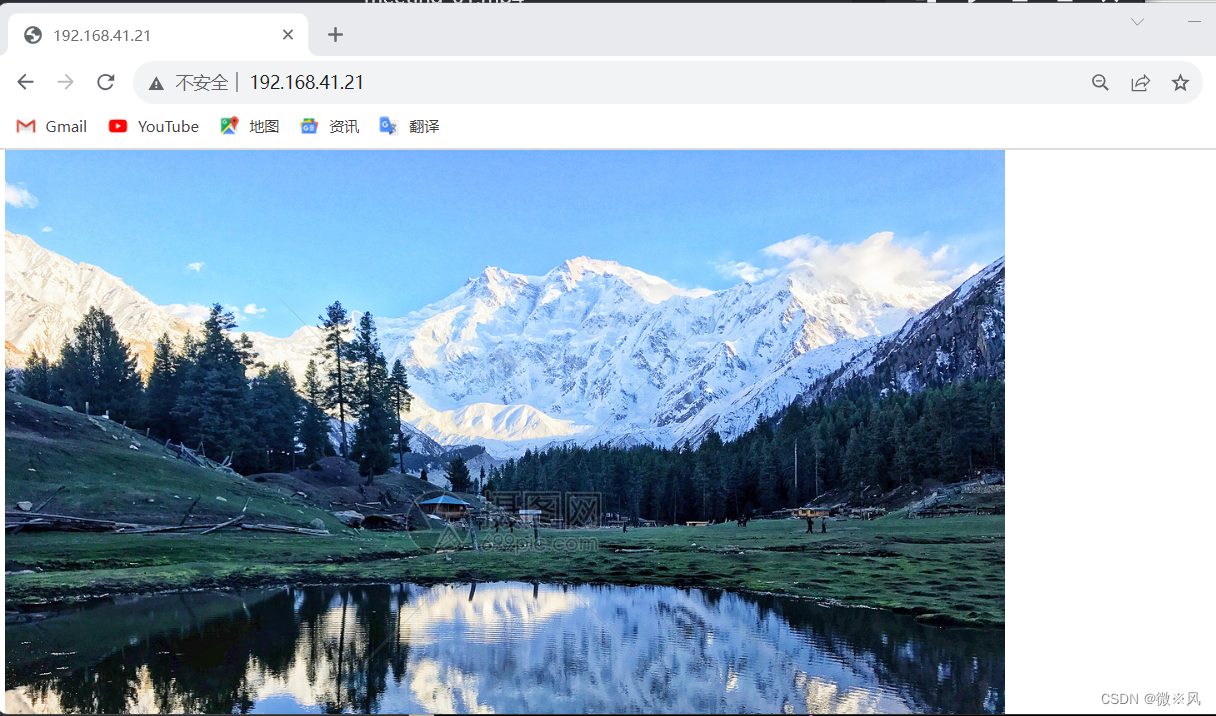
静态页面请求.
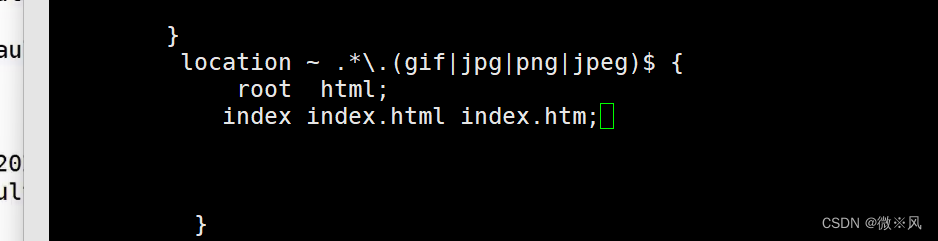
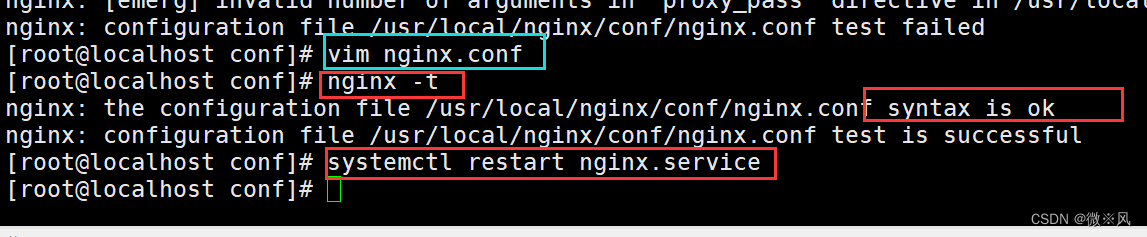
nginx配置完成
tomcat1中建立新目录,设置动态访问内容
编辑访问页面
<%@ page language="java" import="java.util.*" pageEncoding="UTF-8"%>
<html>
<head>
<title>JSP test1 page</title>
</head>
<body>
<% out.println("动态页面 1,http://www.test1.com");%>
</body>
<ml>
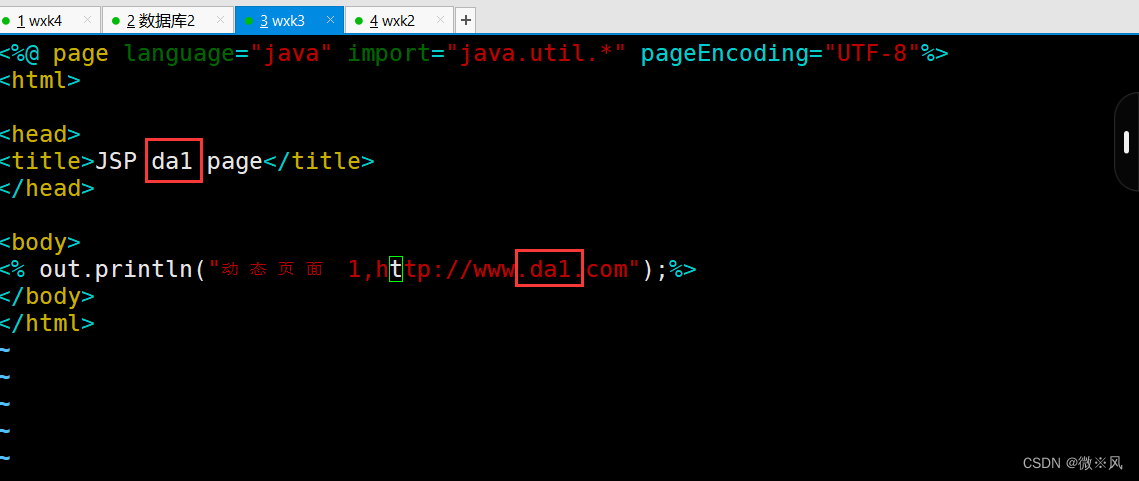
tomcat1 完成
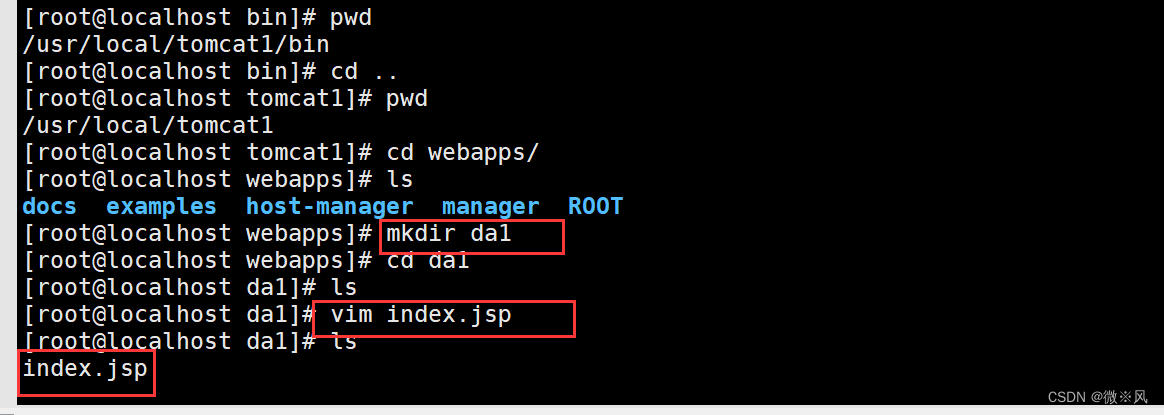
多实例服务器,tomcat2 页面编辑完成
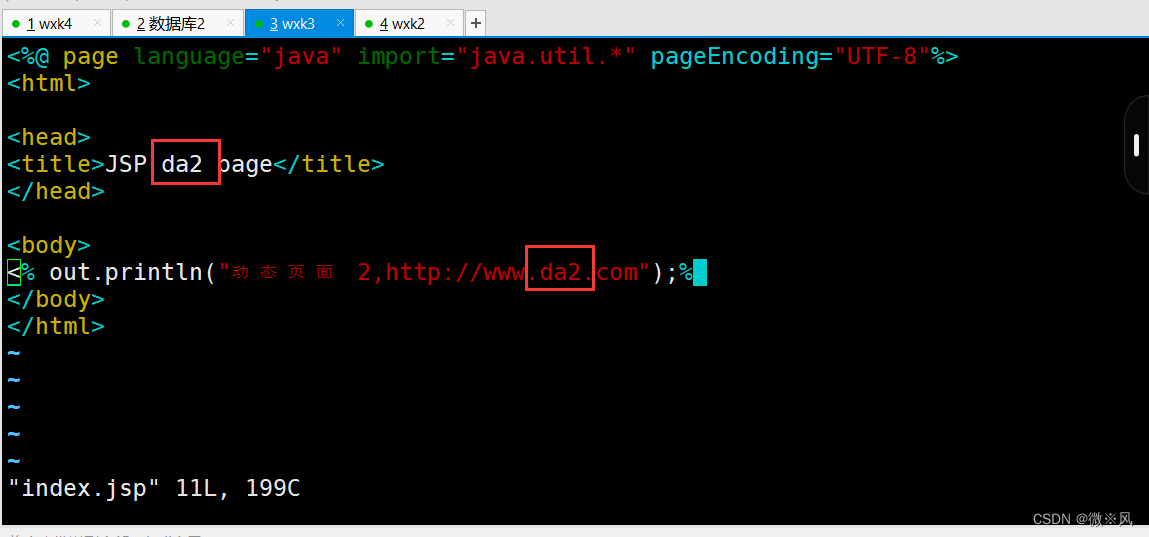
需要进行分离
将其删除
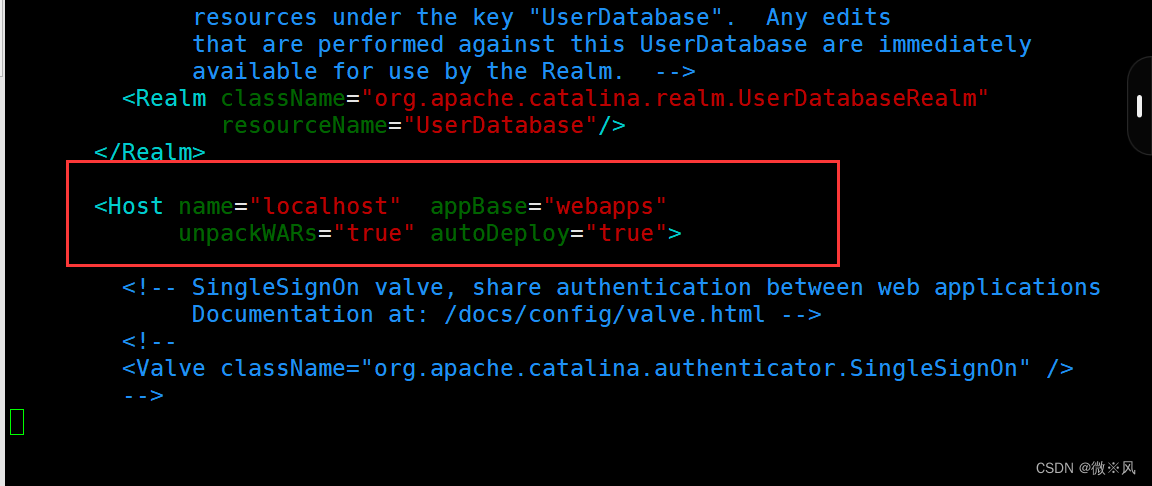
tomcat1设置完成

修改tomcat2 配置 同理先删除不需要的

tomcat2

多实例服务器配置完成
检查tomcat的服务是否正常
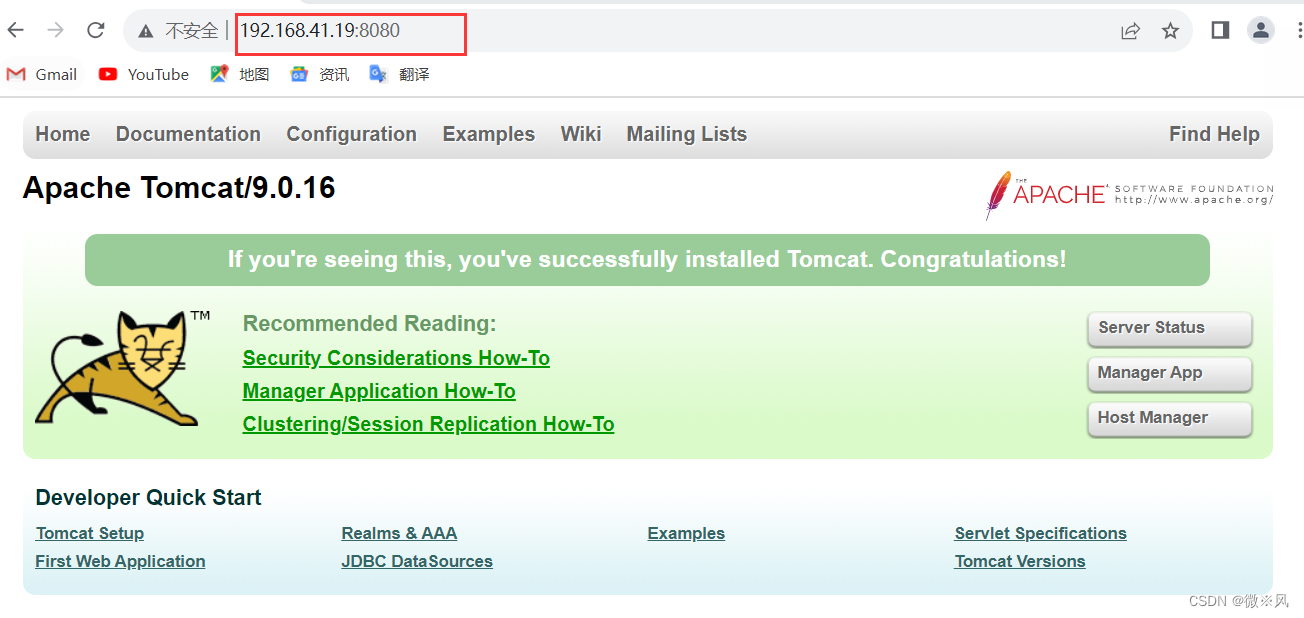
服务正常
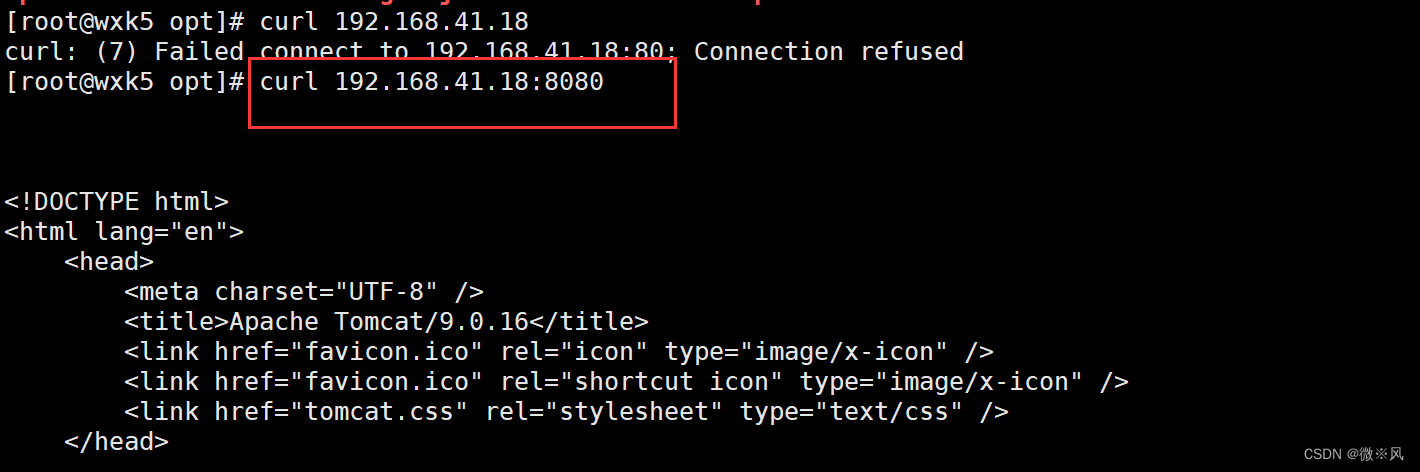
部署19的访问页面
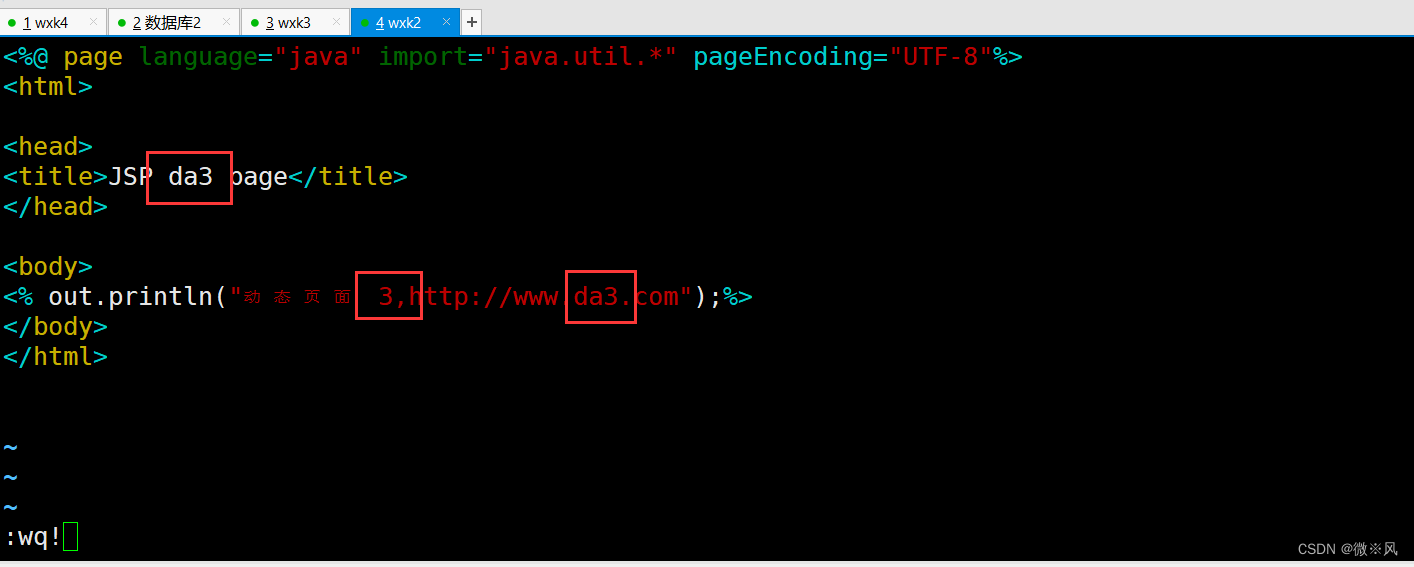
cd /usr/local/
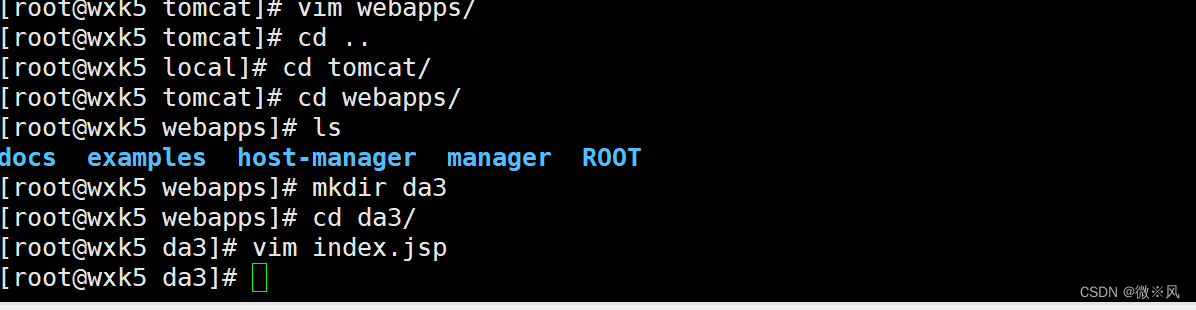
同理将不需要的删除


注意文件位置
重启服务
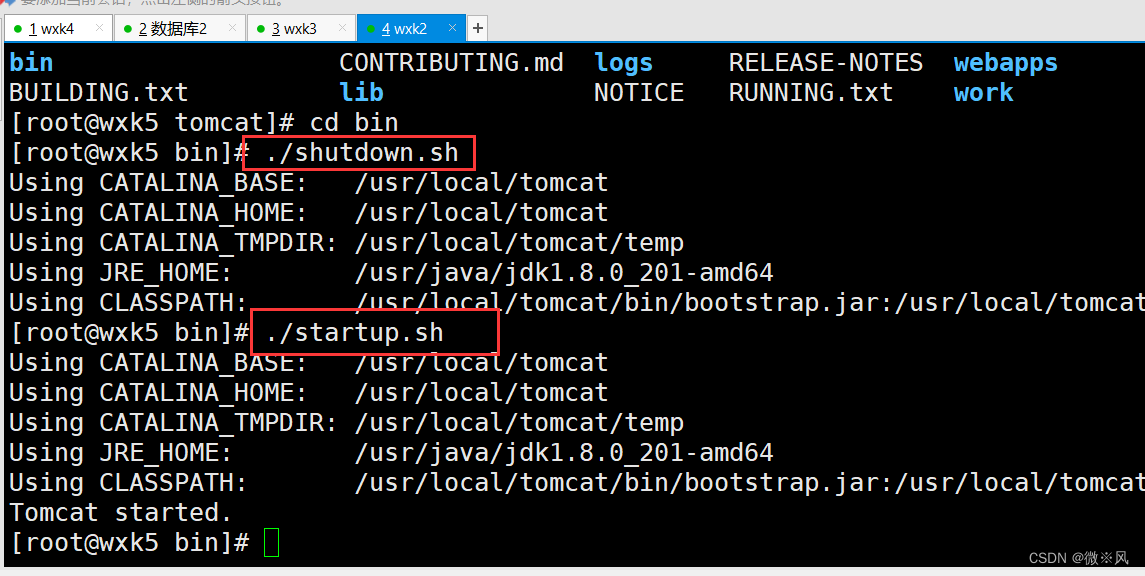
多实例服务也进行重启
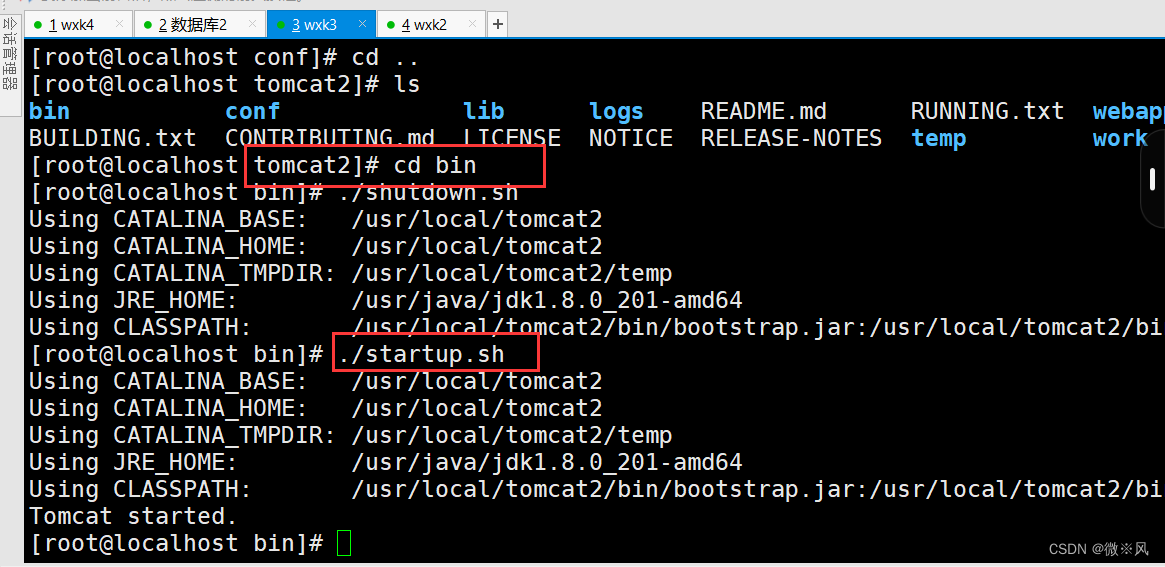
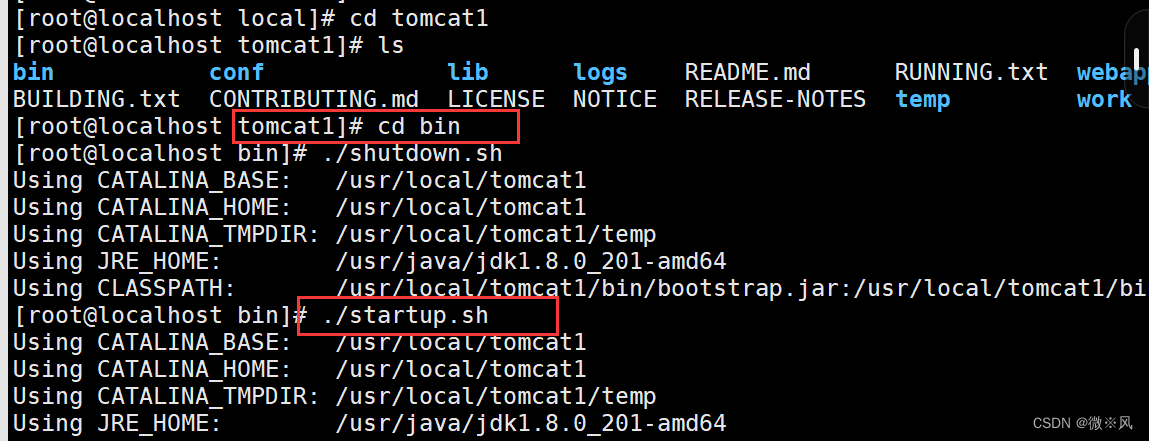

重启完成
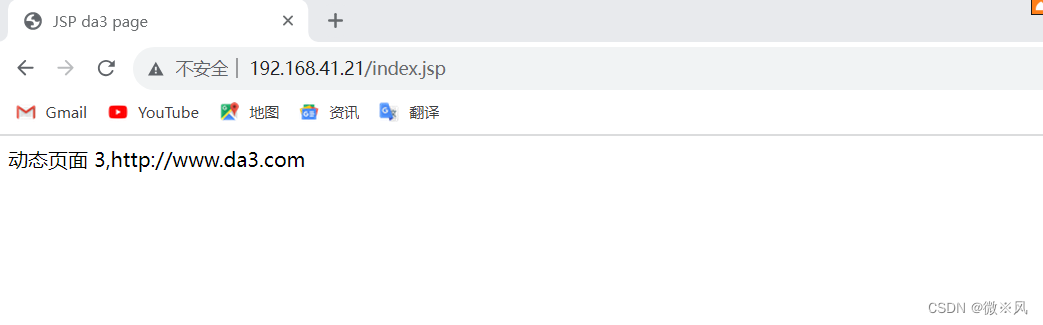
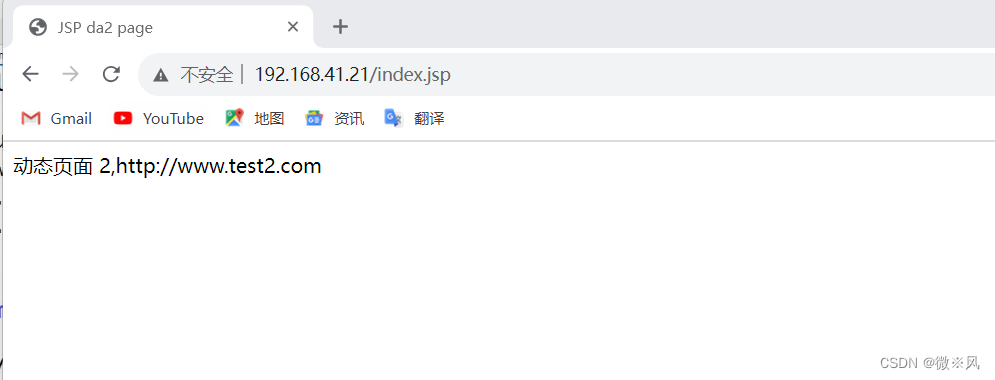
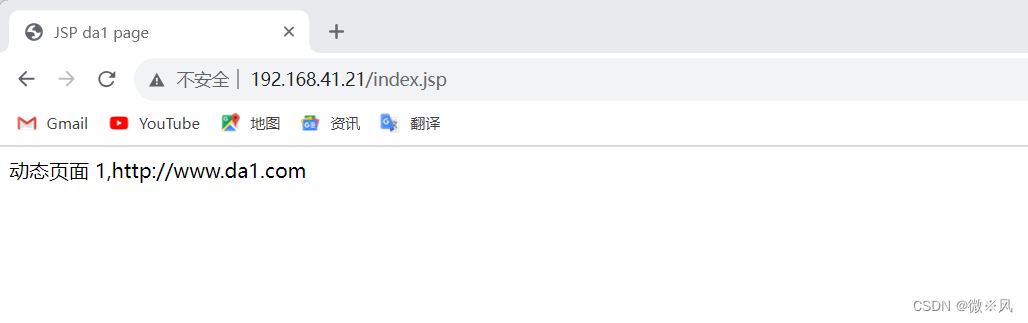
静态访问1