博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持!
博主链接
本人就职于国际知名终端厂商,负责modem芯片研发。
在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。
博客内容主要围绕:
5G/6G协议讲解
算力网络讲解(云计算,边缘计算,端计算)
高级C语言讲解
Rust语言讲解
5G系统消息介绍

系统信息是由基站周期性发送的下行广播信息。系统信息对于移动终端(UE)与基站(gNB)的连接是非常关键的信息。5G环境下,UE上电时读取系统信息进行小区驻留,RRC空闲时读取系统信息进行小区选择和小区重选。系统信息会为终端提供接入网络所需的所有必要信息,如系统帧号、系统带宽、PLMN、小区选择和重选阈值等。
系统信息分类
在5G高层中,系统信息可以分为三类:
- 最少系统信息(Minimum System Information,MSI);
- 剩余最少系统信息(Remaining Minimum System Information,RMSI);
- 其它系统信息(Other System Information,OSI);
这些类别包括MIB和9个SIBs。MIB信息通过BCH和PBCH信道传输,SIBs信息通过DL-SCH和PDSCH信道传输。系统信息与各个信道的映射如下图所示。
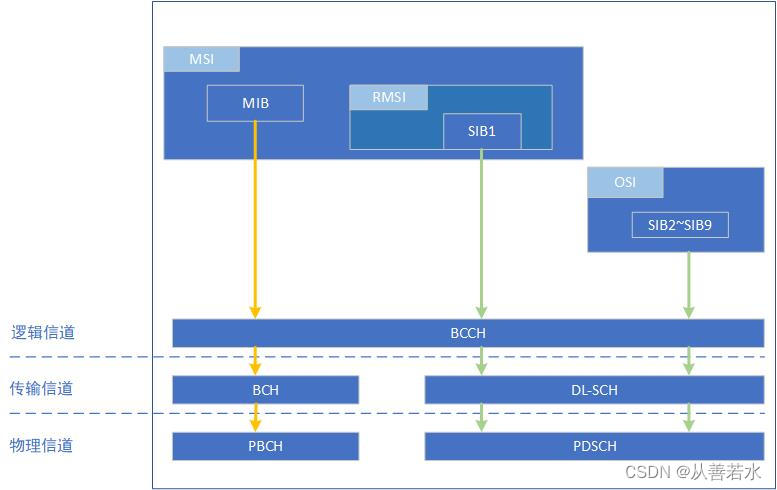
如上图所示,MSI包括MIB和RMSI。RMSI包括SIB1,OSI包括SIB2 ~ SIB9。MIB和SIB1分别有自己的RRC消息 MasterInformationBlock 和 SystemInformationBlock1 ,而SIB2 ~ SIB9被封装在一个称为 SystemInformation 的通用RRC消息中。MSI是周期性广播的,而OSI可以由网络触发或根据终端请求,以广播或以专用方式提供。
当终端需要OSI时,在发送OSI请求之前,终端需要知道在当前小区内需要的OSI是否可以获得,是否可以被广播。当UE处于RRC_IDLE或RRC_INACTIVE时,UE能够在不需要状态转移的情况下请求OSI。对于处于RRC_CONNECTED的UE,可以使用专用的RRC信令来请求和反馈OSI。OSI可以在一定的时间内,按照配置的周期进行广播。OSI是通过广播还是通过UE专用的RRC信令反馈,这是由网络决定的。
UE如何使用MSI
当终端上电后,执行小区搜索过程,解码PSS和SSS信息,得到物理小区ID。然后扫描GSCN处的MIB,获取合适的SS/PBCH block。
MIB信息可以直接通过PBCH信道获取。MIB解码成功后,UE获得了解码SIB1所需的控制资源集(CORSET)和PDCCH搜索空间信息。SIB1提供RACH参数以及关于所有OSI的调度信息。gNB使用 SI-RNTI 对系统信息进行加扰,并使用DCI format 1_0为传输分配PDSCH资源。
以下是3GPP定义的系统信息列表:
| SI | 功能 |
|---|---|
| MIB | 提供SFN、SCS、SIB1 PDCCH资源,小区bar信息 |
| SIB1 | 小区选择信息、PLMN、TAC、小区标识、RAN通知信息、OSI的SI调度信息、服务小区信息 |
| SIB2 | 同频、异频、异系统下的通用小区重选信息 |
| SIB3 | 同频小区重选信息,例如PCI、q-Offset、q-RxLev、q-Qual、小区黑名单 |
| SIB4 | 异频小区重选信息,例如NR-ARFCN |
| SIB5 | 异系统小区重选信息,例如EARFCN |
| SIB6 | 地震和海啸预警系统主要通知 |
| SIB7 | 地震及海啸警报系统次级通知 |
| SIB8 | 商业移动警报服务(CMAS)通知 |
| SIB9 | UTC、GPS和本地时间的计时信息 |