392.判断子序列

力扣题目链接/文章讲解

视频讲解

本题目可以用双指针法来做

class Solution {
public:bool isSubsequence(string s, string t) {// pointer to s, pointer to tint ps = 0, pt = 0; for (pt = 0; pt < t.size(); ++pt) { // 遍历t，在t中按顺序寻找子序列sif (s[ps] == t[pt])ps++;}return ps == s.size();}
};

也可以用动态规划！掌握本题的动态规划解法是对后面要讲解的编辑距离的题目打下基础

动态规划五部曲！

1、确定 dp 数组下标及值含义

dp[i][j]：i 和 j 表示以下标 i 为结尾的字符串 s，和以下标 j 为结尾的字符串 t，值表示这两个字符串最长相同子序列的长度为 dp[i][j]

2、确定递推公式

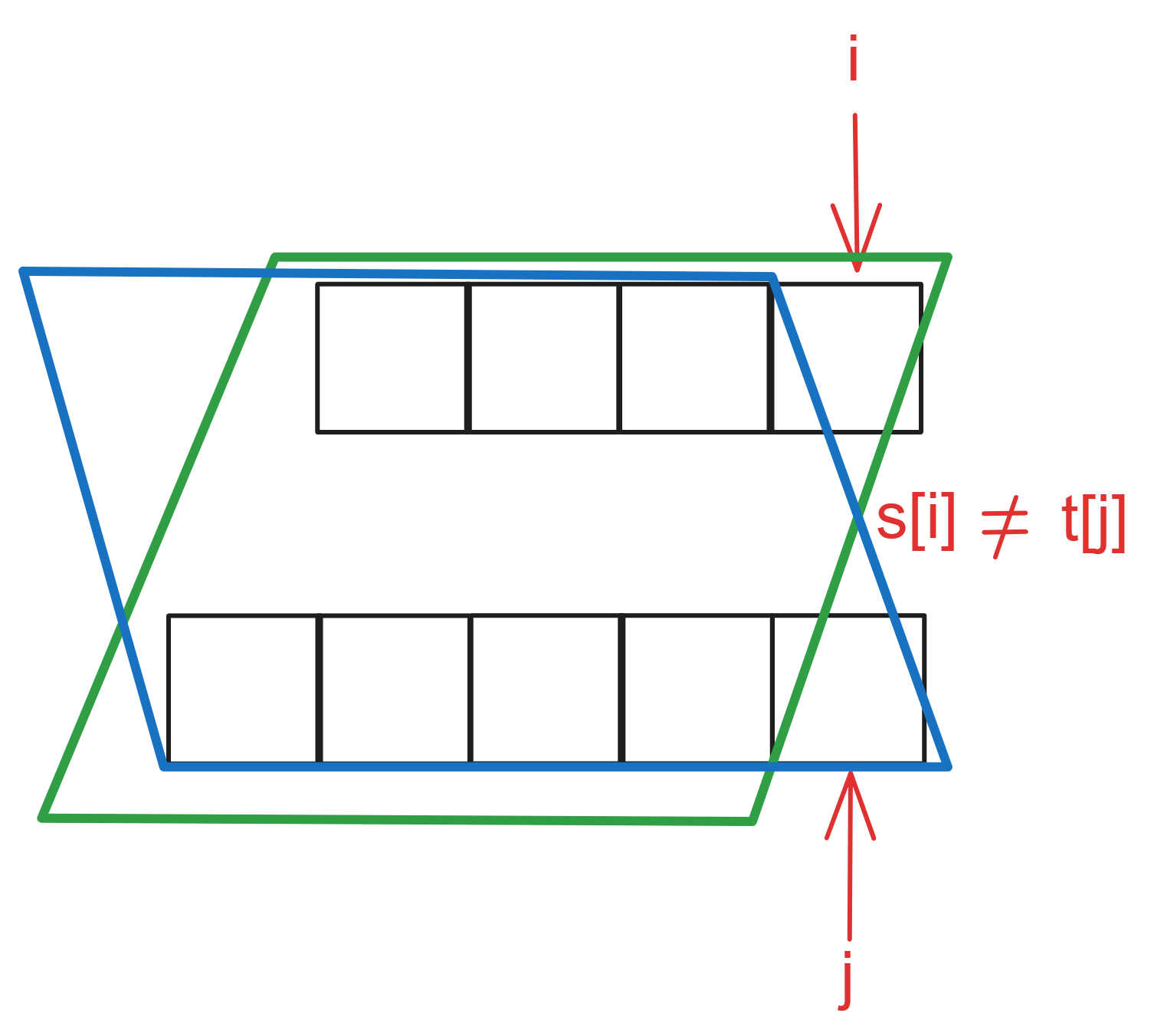
if (s[i] == t[j])，那么 dp[i][j] = dp[i - 1][j - 1] + 1，因为找到了一个相同的字符，相同子序列长度自然要在 dp[i - 1][j - 1] 的基础上加 1（如果不理解，回看一下 dp[i][j] 的定义）

if (s[i] != t[j])，那么 dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])，即 s[0, i] 与 t[0, j] 的最长相同子序列长度一定是 s[0, i - 1] 与 t[0, j] 的最长公共子序列长度或 s[0, i] 与 t[0, j - 1] 的最长公共子序列长度之一，取最大的

3、dp 数组初始化

需要初始化第一行和第一列

dp[0][j] 表示 s[0] 与 t[0, j] 的最长公共子序列长度

dp[i][0] 表示 s[0, i] 与 t[0] 的最长公共子序列长度

4、确定遍历顺序

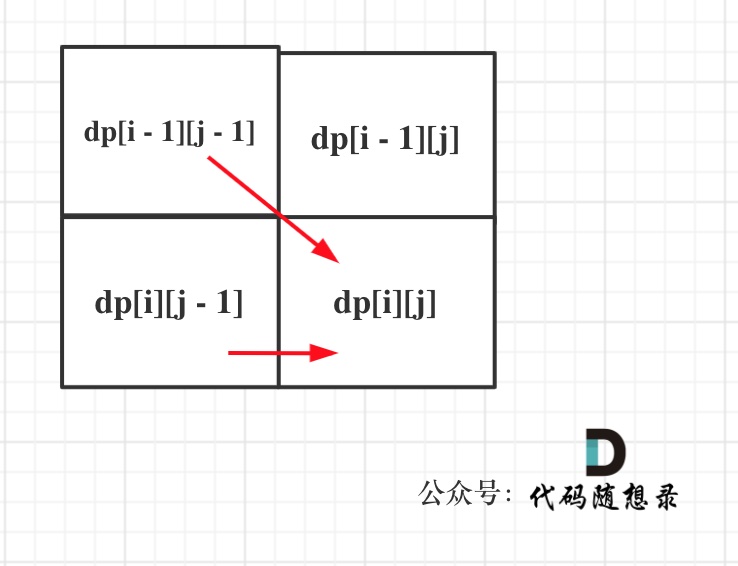
从递推公式可以看出 dp[i][j] 都是依赖于 dp[i - 1][j - 1] 和 dp[i][j - 1]，那么遍历顺序应该是从上到下，从左到右

5、打印 dp 数组验证

最后的结果应该是看两个字符串最长相同子序列的长度是否和 s 的长度相同

代码如下

class Solution {
public:bool isSubsequence(string s, string t) {if (s.size() == 0) return true;if (t.size() == 0) return false;vector<vector<int> > dp(s.size(), vector<int>(t.size(), 1));for (int i = 0; i < s.size(); ++i) {if (s[i] == t[0])break;dp[i][0] = 0;}for (int j = 0; j < t.size(); ++j) {if (s[0] == t[j])break;dp[0][j] = 0;}for (int i = 1; i < s.size(); ++i) {for (int j = 1; j < t.size(); ++j) {if (s[i] == t[j])dp[i][j] = dp[i - 1][j - 1] + 1;elsedp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);}}return dp[s.size() - 1][t.size() - 1] == s.size();}
};

115.不同的子序列

力扣题目链接/文章讲解

视频讲解

1、定义 dp 数组下标及值的含义

我们通过之前的题目已经可以感觉到，对于比较两个数组，需要定义二维的 dp 才能把两个数组中每个元素的比较情况展现出来

dp[i][j]：以下标 i 结尾的 s 含有以下标 j 结尾的 t 的个数

2、确定递推公式

考虑串 s[0, i] 有多少种方式含有 t[0, j]

首先，如果 s[i] != t[j]

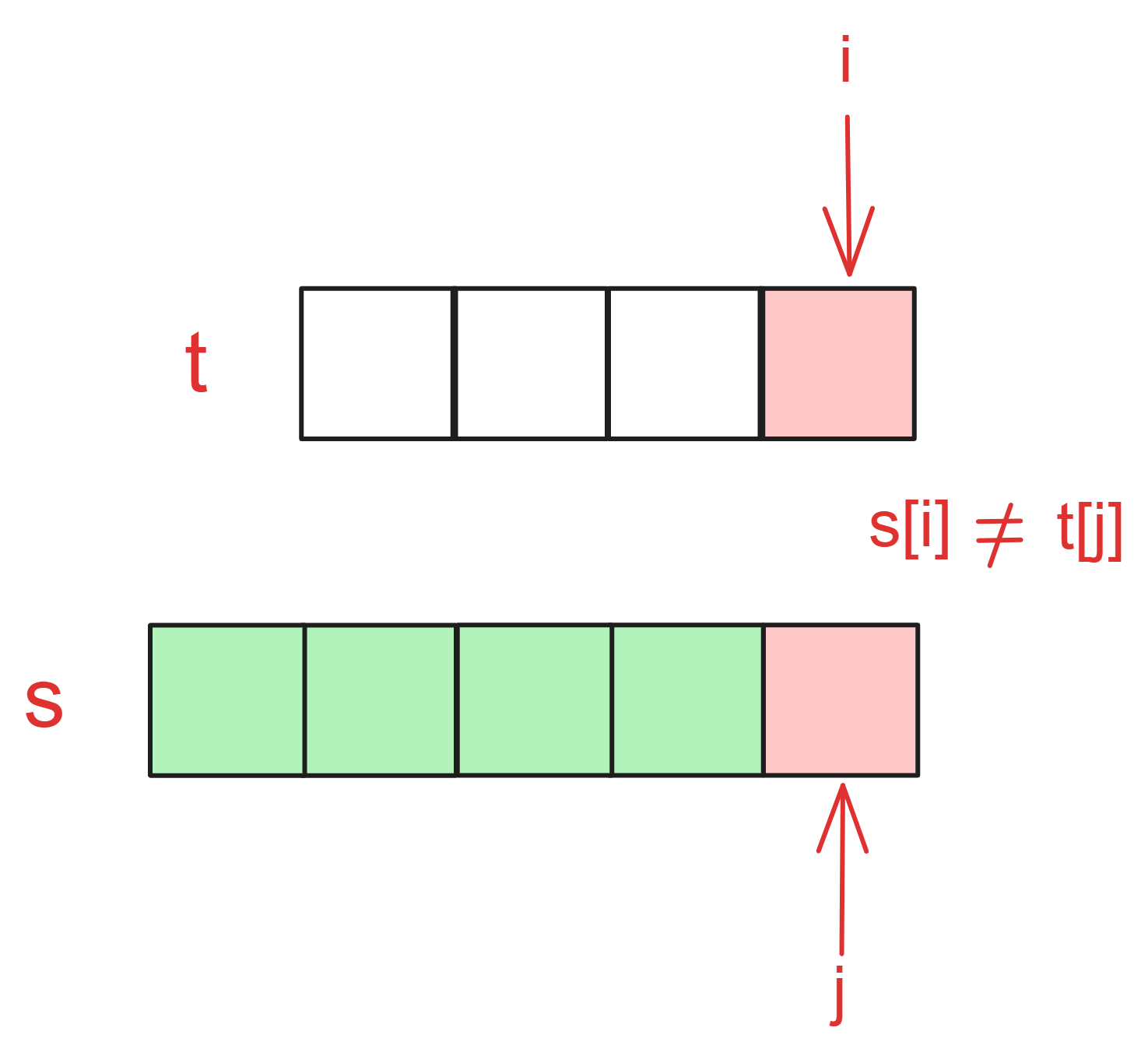
那么 s[0, i] 有含有 t[0, j] 的方式数，与 s[0, i - 1] 含有 t[0, j] 的方式数相等，即 dp[i][j] = dp[i - 1][j]

如果 s[i] == t[j]

那么 s[0, i] 有含有 t[0, j] 的有两种情况

s[0, i - 1] 已经含有 t[0, j] 了

这种情况的方式数量为 dp[i - 1][j]

s[0, i - 1] 含有 t[0, j - 1]，即 s[i] 与 t[j] 匹配

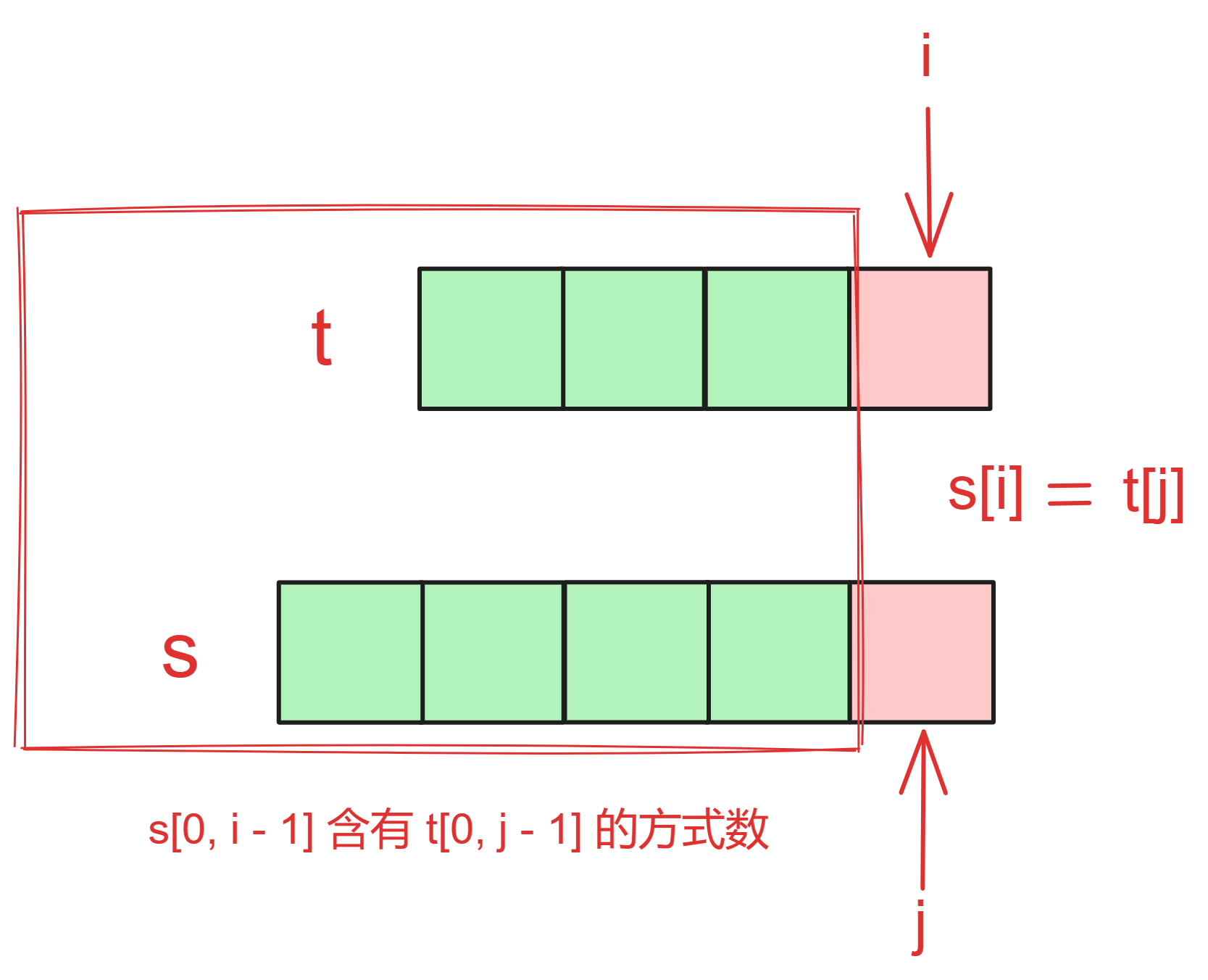
这种情况的方式数量为 dp[i - 1][j - 1]

需要对这两种 s[i] == t[j] 下的情况求和

if (s[i] != t[j])dp[i][j] = dp[i - 1][j];
else if (s[i] == t[j])dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];

3、dp 数组初始化

初始化第一列和第一行

第一列：dp[i][0]，即以下标 i 结尾的 s 含有 t[0] 的个数

第一行：dp[0][j]，即 s[0] 含有 t[0, j] 的个数，当 j 大于 0 时一定为 0，dp[0][0] 为 0 或 1

4、确定遍历顺序

根据递推公式，从上往下从左往右遍历填充 dp 数组

5、打印 dp 数组验证

class Solution {
public:int numDistinct(string s, string t) {if (s.size() == 0) return 0;vector<vector<uint64_t> > dp(s.size(), vector<uint64_t>(t.size(), 0));int num = 0;for (int i = 0; i < s.size(); ++i) {    // dp[i][0]if (s[i] == t[0])++num;dp[i][0] = num;}// dp[0][j]if (t[0] == s[0])dp[0][0] = 1; for (int i = 1; i < s.size(); ++i) {for (int j = 1; j < t.size(); ++j) {if (s[i] != t[j])dp[i][j] = dp[i - 1][j];else if (s[i] == t[j])dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];}}return dp[s.size() - 1][t.size() - 1];}
};