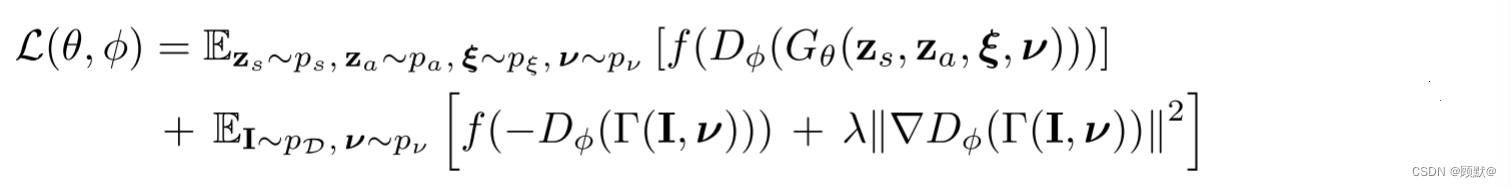ARIMA模型是一种常用的时间序列预测模型,全称为自回归积分滑动平均模型(Autoregressive Integrated Moving Average model)。下面是一个使用MATLAB进行ARIMA模型预测的基本示例。请注意,这是一个基础示例,实际应用中可能需要更复杂的数据预处理和模型调整。
matlab">% 假设你有一个名为'timeSeriesData'的时间序列数据向量
% 首先,我们需要导入或创建这个时间序列数据
% 例如,这里我们简单地创建一个随机的时间序列数据
rng('default'); % 为了结果的可复现性
timeSeriesData = randn(1, 100); % 生成一个包含100个随机数的向量% 使用MATLAB的内置函数fitarima来拟合ARIMA模型
% 我们假设ARIMA模型的阶数为(2, 1, 1),这只是一个示例,实际中你需要通过一些方法(如AIC准则)来确定最佳的阶数
Mdl = arima('ARLags',1:2,'D',1,'MALags',1);% 使用fit函数来拟合模型
EstMdl = estimate(Mdl, timeSeriesData);% 现在,我们可以使用这个模型来进行预测
% 假设我们想要预测接下来的10个时间点的值
numSteps = 10;
[YF, YMSE] = forecast(EstMdl, numSteps, 'Y0', timeSeriesData);% 显示预测结果
disp('Forecasted Values:');
disp(YF);% 显示预测误差的均方根
disp('Forecast Mean Squared Error:');
disp(YMSE);% 为了可视化结果,我们可以绘制原始数据和预测数据
figure;
hold on;
plot(timeSeriesData, 'b'); % 原始数据
h1 = plot(numel(timeSeriesData)+(1:numSteps), YF, 'r--'); % 预测数据
xlabel('Time');
ylabel('Value');
legend('Original Data', 'Forecasted Values', 'Location', 'Best');
hold off;
在这个例子中,我们首先创建了一个随机的时间序列数据。然后,我们假设了一个ARIMA模型的阶数,并使用fitarima函数创建了一个ARIMA模型对象。接着,我们使用estimate函数来拟合模型,并使用forecast函数来预测未来的值。最后,我们显示了预测结果,并绘制了原始数据和预测数据的图表。
需要注意的是,ARIMA模型的阶数(即AR的阶数、差分的阶数和MA的阶数)的选择对模型的预测性能有很大的影响。在实际应用中,通常需要通过一些方法来确定最佳的阶数,例如通过比较不同阶数模型的AIC(赤池信息准则)或BIC(贝叶斯信息准则)值。此外,还需要检查模型的残差,以确保它们是随机的并且没有显著的自相关。
此外,这个示例假设你的时间序列数据是平稳的。如果数据不是平稳的,你可能需要先进行差分或其他转换,以使数据变得平稳。ARIMA模型对平稳性有严格的要求,因为非平稳数据可能会导致模型的不稳定和无效的预测。
以上是一个基本的ARIMA模型预测在MATLAB中的实现。根据你的具体需求和数据特性,可能需要进行更复杂的调整和优化。