相关文章
创建第一个Springboot项目HelloWorld
目录 一、准备工作 一、创建springboot项目 三、使用git上传到代码仓库gitee 四、git使用过程问题总结 一、准备工作
安装jdk:8u201(可以使用高一点的版本)
jdk所有版本下载:Java Archive | Oracle
安装maven:不用…
gigachad - suid
gigachadeasyftp利用、google反图搜索、 suid提权、s-nail 提权
主机发现
┌──(kali㉿kali)-[~/桌面/OSCP]
└─$ sudo netdiscover -i eth0 -r 192.168.44.138/24服务探测
┌──(kali㉿kali)-[~/桌面/OSCP]
└─$ sudo nmap -sV -A -T 4 -p- 192.168.44.138 |_/kingchad…
Swift开发——索引器扩展
扩展用于向已存在的类型(例如,类、结构体、枚举和协议等)中添加新的功能,扩展甚至可以向系统类型(包括无法查阅代码的类型)中添加新的功能,但是扩展不能覆盖原类型中已有的方法,扩展也不能向类中添加新的存储属性。 01、索引器扩展 扩展可为类、结构体等类型添加索引器。程序段…
Spring 系统架构图
Spring 系统架构图 Spring Framework是Spring生态圈中最基础的项目,是其他项目的根基。 Spring Framework的发展也经历了很多版本的变更,每个版本都有相应的调整 Spring Framework的5版本目前没有最新的架构图,而最新的是4版本,…
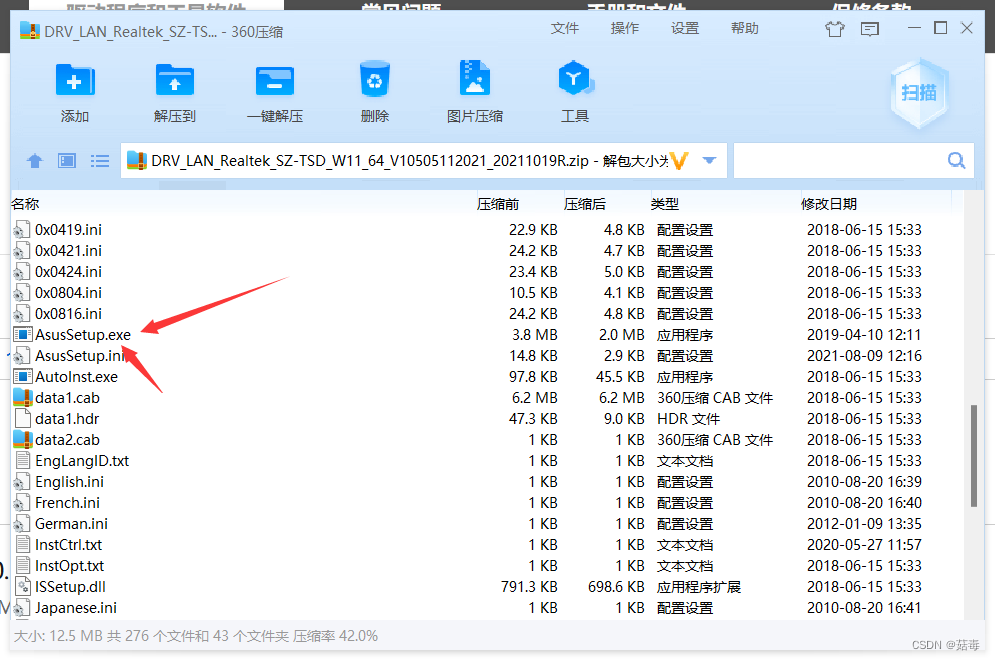
安装台式电脑网卡驱动
安装电脑网卡驱动 1. 概述2. 具体方法2.1 先确定主板型号2.2 详细操作步骤如下2.2.1 方法一2.2.2 方法二2.2 主流主板官网地址 结束语 1. 概述
遇到重装系统后、或者遇到网卡驱动出现问题没有网络时,当不知道怎么办时,以下的方法,可以作为一…
别害怕冲突 - 建立良好的关系
任何事都以基本要素为基础。也就是说,所有专业知识都是建立在基础知识之上。
那么,想要有效处理分歧,你首先要明确沟通的基本要素。避免频繁遭遇沮丧,或者谈话脱轨导致彼此。
有效处理分歧的基本要素,大部分都可以归…
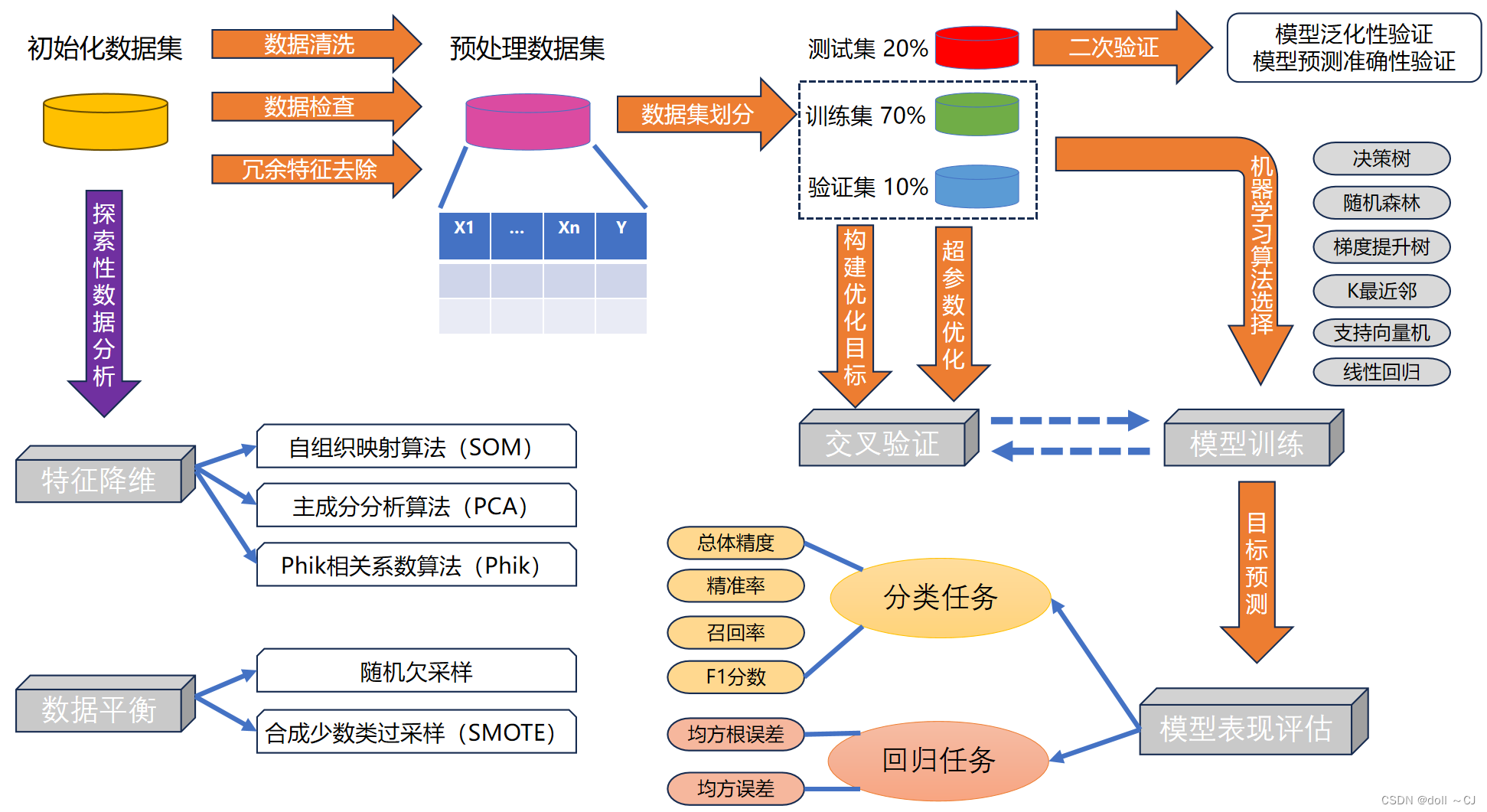
基于scikit-learn的机器学习分类任务实践——集成学习
一、传统机器学习分类流程与经典思想算法简述 传统机器学习是指,利用线性代数、数理统计与优化算法等数学方式从设计获取的数据集中构建预测学习器,进而对未知数据分类或回归。其主要流程大致可分为七个部分,依次为设计获取数据特征集&#x…